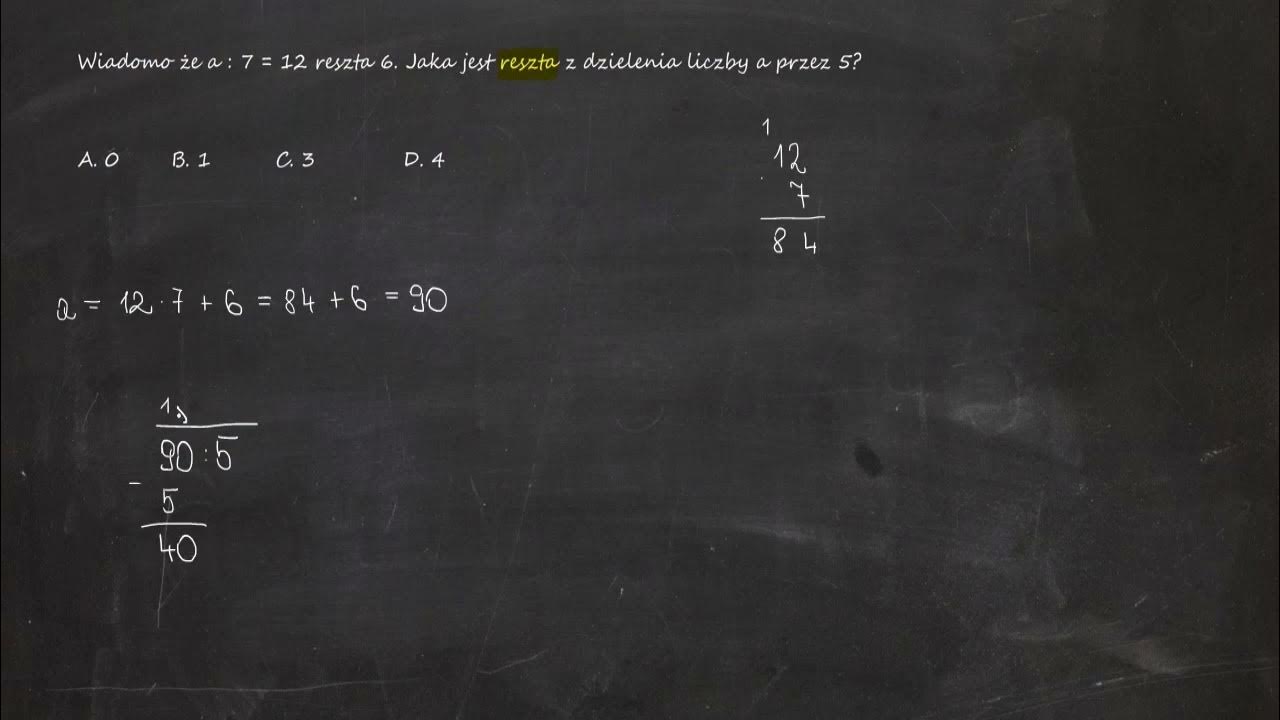Reszta Z Dzielenia Przez 5

Czy kiedykolwiek zastanawiałeś się, co naprawdę kryje się za tym, co zostaje nam "na boku", gdy dzielimy liczbę przez 5? To, co na pierwszy rzut oka może wydawać się prostym działaniem matematycznym, w rzeczywistości otwiera drzwi do fascynującego świata regularności i wzorców. W tym artykule zgłębimy temat reszty z dzielenia przez 5, pokazując, jak to pojęcie znajduje zastosowanie nie tylko w matematyce, ale i w życiu codziennym. Artykuł ten jest skierowany do wszystkich, którzy chcą lepiej zrozumieć podstawy matematyki, a szczególnie do uczniów szkół podstawowych i średnich, oraz do każdego, kto szuka praktycznych zastosowań wiedzy matematycznej.

Czym jest reszta z dzielenia?

Zanim przejdziemy do szczegółów dotyczących dzielenia przez 5, upewnijmy się, że rozumiemy fundamentalne pojęcie reszty z dzielenia. Gdy dzielimy jedną liczbę (dzielną) przez drugą (dzielnik), otrzymujemy iloraz i resztę. Iloraz to liczba całkowita, która pokazuje, ile razy dzielnik mieści się w dzielnej, a reszta to to, co zostaje, gdy nie możemy już dzielić dalej, zachowując liczby całkowite. Na przykład, dzieląc 17 przez 5, otrzymujemy iloraz 3 i resztę 2, ponieważ 5 mieści się w 17 trzy razy (5 x 3 = 15), a pozostaje nam 2 (17 - 15 = 2).

Dlaczego reszta jest ważna?

Reszta, choć często pomijana, jest niezwykle istotna. Pozwala nam zrozumieć, jak blisko dana liczba jest podzielna przez inną. W przypadku reszty z dzielenia przez 5, pomaga nam szybko zidentyfikować liczby, które są bliskie wielokrotności 5. To z kolei ma praktyczne implikacje, które zobaczymy w dalszej części artykułu.

Reszta z dzielenia przez 5: Kluczowe cechy

Dzieląc liczbę przez 5, reszta może przyjąć jedną z pięciu wartości: 0, 1, 2, 3 lub 4. Nigdy nie będzie równa 5 ani większa, ponieważ wtedy moglibyśmy jeszcze raz podzielić przez 5.

Reszta 0: Oznacza, że liczba jest podzielna przez 5. Na przykład, 10, 15, 20, 25 to liczby podzielne przez 5.
Reszta 1: Oznacza, że liczba jest o 1 większa od wielokrotności 5. Na przykład, 6, 11, 16, 21.
Reszta 2: Oznacza, że liczba jest o 2 większa od wielokrotności 5. Na przykład, 7, 12, 17, 22.
Reszta 3: Oznacza, że liczba jest o 3 większa od wielokrotności 5. Na przykład, 8, 13, 18, 23.
Reszta 4: Oznacza, że liczba jest o 4 większa od wielokrotności 5. Na przykład, 9, 14, 19, 24.

Szybkie sprawdzanie reszty

Istnieje prosty sposób na szybkie sprawdzenie reszty z dzielenia przez 5, bez konieczności wykonywania pełnego dzielenia. Wystarczy spojrzeć na ostatnią cyfrę liczby:

Jeśli ostatnia cyfra to 0 lub 5, reszta z dzielenia przez 5 wynosi 0.
Jeśli ostatnia cyfra to 1 lub 6, reszta z dzielenia przez 5 wynosi 1.
Jeśli ostatnia cyfra to 2 lub 7, reszta z dzielenia przez 5 wynosi 2.
Jeśli ostatnia cyfra to 3 lub 8, reszta z dzielenia przez 5 wynosi 3.
Jeśli ostatnia cyfra to 4 lub 9, reszta z dzielenia przez 5 wynosi 4.

Na przykład, spójrzmy na liczbę 1234. Ostatnia cyfra to 4, więc reszta z dzielenia 1234 przez 5 wynosi 4. To naprawdę proste, prawda?

Praktyczne zastosowania reszty z dzielenia przez 5

Wiedza o reszcie z dzielenia przez 5 może być zaskakująco przydatna w różnych sytuacjach życiowych.

1. Szybkie obliczenia

Wyobraź sobie, że jesteś w sklepie i musisz szybko oszacować, czy masz wystarczająco pieniędzy. Możesz wykorzystać znajomość reszty z dzielenia przez 5, aby przybliżyć koszt kilku produktów. Na przykład, jeśli kupujesz 7 produktów, których ceny kończą się na "zł 2", możesz szybko oszacować, że suma końcówek to 14 zł. Dzieląc 14 przez 5, otrzymujesz resztę 4. Oznacza to, że suma końcówek będzie zbliżona do wielokrotności 5 plus 4 zł, co ułatwia oszacowanie całkowitego kosztu.

2. Planowanie i organizacja

Załóżmy, że planujesz podział zadań w grupie pięcioosobowej. Możesz wykorzystać resztę z dzielenia, aby zapewnić równomierny podział pracy. Jeśli masz 27 zadań, możesz podzielić je tak, aby każda osoba otrzymała 5 zadań, a pozostałe 2 rozdzielić losowo lub przydzielić osobom, które mają więcej czasu. Reszta z dzielenia przez 5 pomaga w sprawiedliwym i efektywnym rozdzielaniu zasobów.

3. Kryptografia i kody

W kryptografii, reszta z dzielenia (znana jako operacja modulo) jest szeroko stosowana. Choć bezpośrednie zastosowanie reszty z dzielenia przez 5 może nie być powszechne w zaawansowanych algorytmach, to koncepcja ta jest fundamentem wielu bardziej skomplikowanych operacji. Na przykład, w prostych szyfrach, reszta z dzielenia może być używana do przesuwania liter alfabetu. Jeśli chcemy zaszyfrować literę "A" przesuwając ją o 3 pozycje, a alfabet ma 26 liter, możemy użyć reszty z dzielenia (3 + pozycja litery A) przez 26. To podstawowa, ale ważna koncepcja.

4. Zabawy matematyczne i gry

Reszta z dzielenia przez 5 może być wykorzystywana w różnych grach i zabawach matematycznych. Możemy tworzyć zagadki, w których trzeba odgadnąć liczbę na podstawie reszty z dzielenia przez 5 i innych wskazówek. To świetny sposób na rozwijanie logicznego myślenia i umiejętności matematycznych w sposób angażujący i zabawny.

5. Codzienne decyzje

Zastanów się, jak często musisz podejmować decyzje dotyczące podziału, grupowania lub szacowania. Znajomość reszty z dzielenia przez 5 może pomóc Ci w podejmowaniu tych decyzji szybciej i bardziej efektywnie. Na przykład, jeśli musisz podzielić 23 jabłka między 5 osób, od razu wiesz, że każda osoba dostanie 4 jabłka, a 3 zostaną na później.

Przykłady z życia wzięte

Przykład 1: Masz 37 ciasteczek i chcesz sprawiedliwie rozdać je wśród 5 przyjaciół. Dzieląc 37 przez 5, otrzymujesz iloraz 7 i resztę 2. Oznacza to, że każdy z Twoich przyjaciół otrzyma 7 ciasteczek, a Tobie zostaną 2.

Przykład 2: Organizujesz wycieczkę szkolną i musisz podzielić 68 uczniów na 5 równych grup. Dzieląc 68 przez 5, otrzymujesz iloraz 13 i resztę 3. To znaczy, że możesz utworzyć 5 grup po 13 uczniów, a 3 uczniów będą musieli dołączyć do jednej z tych grup (tworząc grupę 14-osobową).

Przykład 3: Pracujesz w magazynie i musisz spakować 149 długopisów do paczek po 5 sztuk. Dzieląc 149 przez 5, otrzymujesz iloraz 29 i resztę 4. Oznacza to, że uda Ci się spakować 29 pełnych paczek, a 4 długopisy zostaną niespakowane.

Podsumowanie i korzyści

Jak widzimy, reszta z dzielenia przez 5 to proste, ale potężne narzędzie, które może być przydatne w wielu sytuacjach. Pozwala nam szybko szacować, dzielić i organizować, a także rozwijać umiejętności matematyczne i logiczne myślenie. Pamiętajmy, że matematyka to nie tylko abstrakcyjne wzory i równania, ale przede wszystkim narzędzie do rozwiązywania problemów i ułatwiania życia. Zachęcamy do dalszego eksplorowania fascynującego świata matematyki i odkrywania jego praktycznych zastosowań. Zrozumienie reszty z dzielenia przez 5 to pierwszy krok do opanowania bardziej zaawansowanych koncepcji matematycznych.

Pamiętaj, matematyka jest wszędzie wokół nas. Wystarczy otworzyć oczy i zacząć ją dostrzegać! Ucząc się podstaw, budujemy solidny fundament do dalszego rozwoju i sukcesów, zarówno w szkole, jak i w życiu codziennym. Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć pojęcie reszty z dzielenia przez 5 i zainspirował do dalszego poszerzania swojej wiedzy matematycznej.