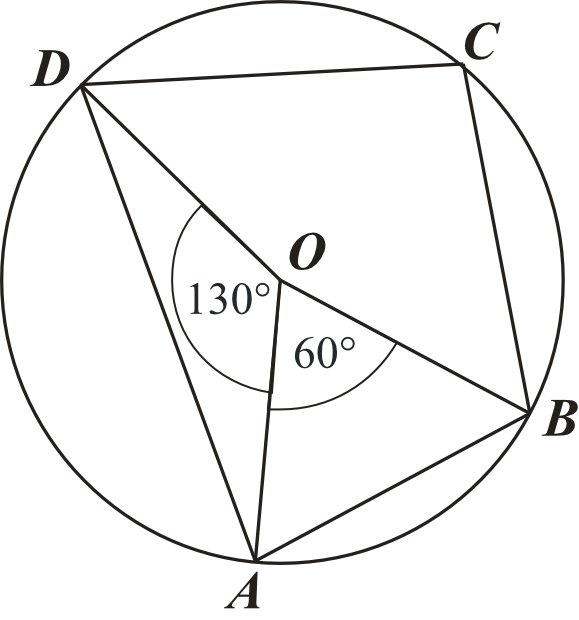
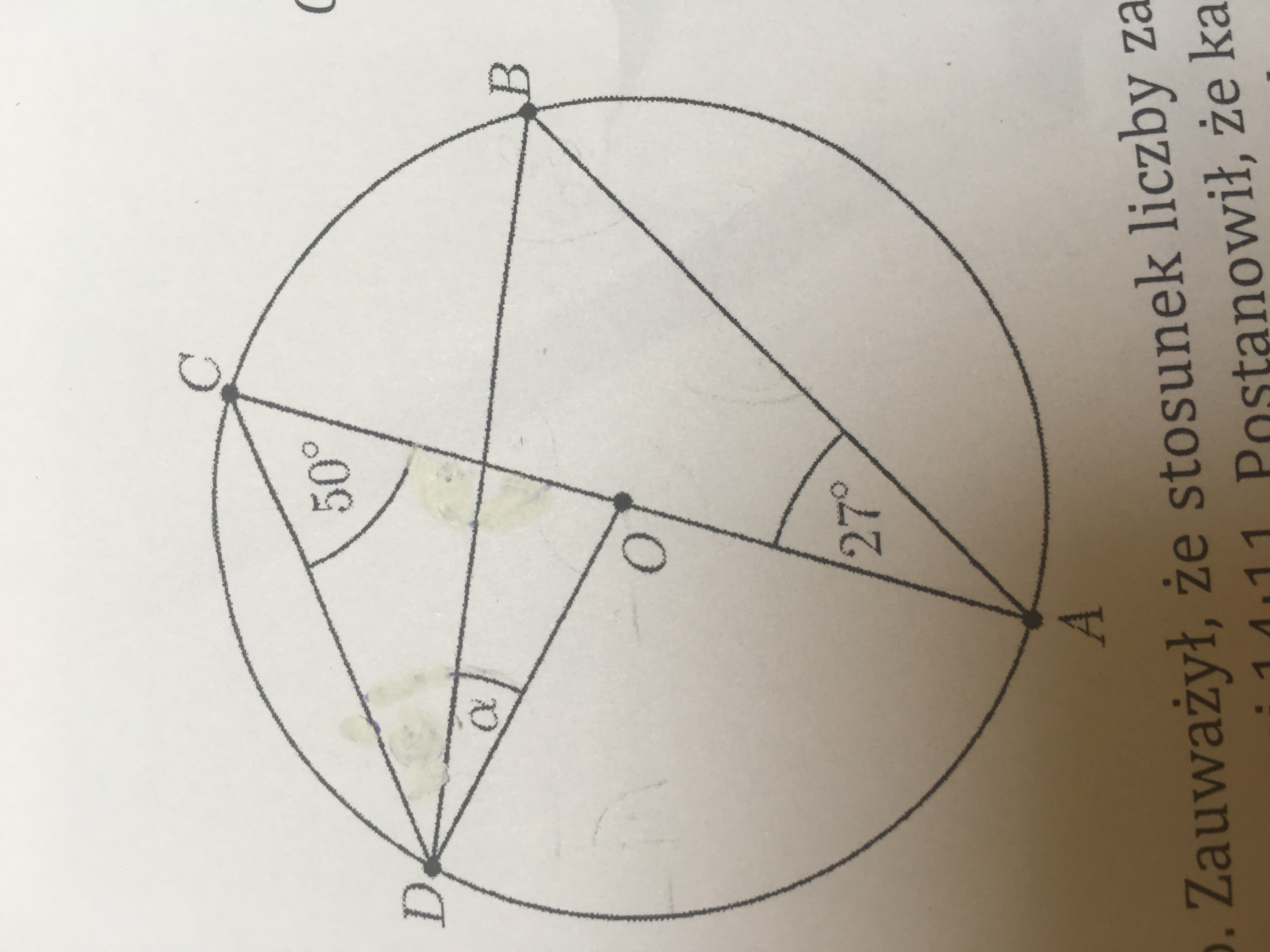
Punkt O Jest środkiem Okręgu Kąt Wpisany Alfa Ma Miarę

Dobrze, postaram się wyjaśnić to zagadnienie w sposób prosty i zrozumiały. Często sprawia ono problemy na początku nauki geometrii, więc przejdźmy do konkretów.

Mamy okrąg. Wyobraź sobie idealnie okrągły placek. W samym środku tego placka znajduje się punkt. Nazywamy go punktem O i mówimy, że jest on środkiem okręgu. Czyli O to po prostu "centrum dowodzenia" naszego okręgu.

Teraz wyobraź sobie, że masz kąt, który wierzchołek (czyli ten "szpic") leży na okręgu (na krawędzi naszego placka). Ramiona tego kąta przecinają okrąg w dwóch różnych punktach. Taki kąt nazywamy kątem wpisanym. Ważne, żeby ten wierzchołek leżał na okręgu, a nie gdzieś w środku, ani na zewnątrz. Kąt wpisany "wpisuje się" w okrąg. Miarę tego kąta, czyli jak bardzo jest on otwarty, oznaczamy grecką literą alfa (α).

Co to oznacza? Mówimy, że kąt wpisany α ma jakąś miarę (np. 30 stopni, 60 stopni, 90 stopni itd.). Czyli po prostu wiemy, jak bardzo ten kąt jest "rozwarty".

Związek kąta wpisanego z kątem środkowym

Teraz pojawia się najciekawsza część. Wyobraź sobie drugi kąt. Jego wierzchołek leży w środku okręgu (w punkcie O). Ramiona tego kąta również przecinają okrąg w tych samych dwóch punktach, co ramiona naszego kąta wpisanego α. Taki kąt nazywamy kątem środkowym, ponieważ jego wierzchołek jest w środku okręgu.

Kąt środkowy, oparty na tym samym łuku okręgu co kąt wpisany α, ma pewną bardzo ważną cechę: jego miara jest dwa razy większa niż miara kąta wpisanego α.

Czyli:

• Jeśli kąt wpisany α ma 30 stopni, to kąt środkowy oparty na tym samym łuku ma 60 stopni.
• Jeśli kąt wpisany α ma 45 stopni, to kąt środkowy oparty na tym samym łuku ma 90 stopni.
• Jeśli kąt wpisany α ma 60 stopni, to kąt środkowy oparty na tym samym łuku ma 120 stopni.

I tak dalej. To bardzo ważna zasada, która często przydaje się przy rozwiązywaniu zadań z geometrii. Pamiętaj, że ta zasada działa tylko wtedy, gdy oba kąty (wpisany i środkowy) są oparte na tym samym łuku. To znaczy, że ich ramiona przecinają okrąg w tych samych dwóch punktach.

Wyobraź sobie, że masz kawałek ciasta w kształcie wycinka koła. Kąt środkowy to kąt wyznaczony przez boki tego wycinka, spotykające się w środku placka. Kąt wpisany to kąt, którego wierzchołek leży na krawędzi placka (na łuku wycinka), a ramiona sięgają do tych samych punktów, co ramiona kąta środkowego. Kąt wpisany będzie "węższy" niż kąt środkowy.

Przykłady i Zastosowania

Żeby to lepiej zrozumieć, przejdźmy do kilku przykładów:

1. Zadanie: W okręgu o środku O kąt wpisany α ma miarę 25 stopni. Oblicz miarę kąta środkowego, opartego na tym samym łuku.

   Rozwiązanie: Kąt środkowy ma miarę 2 * α = 2 * 25 = 50 stopni.

2. Zadanie: W okręgu o środku O kąt środkowy, oparty na pewnym łuku, ma miarę 110 stopni. Oblicz miarę kąta wpisanego α, opartego na tym samym łuku.

   Rozwiązanie: Kąt wpisany ma miarę 110 / 2 = 55 stopni.

3. Zadanie: Dany jest okrąg o środku O. Kąt wpisany α oparty na pewnym łuku ma miarę x. Kąt środkowy oparty na tym samym łuku ma miarę 3x - 40. Oblicz miarę kąta α.

   Rozwiązanie: Wiemy, że kąt środkowy jest dwa razy większy od kąta wpisanego, więc 3x - 40 = 2x. Odejmując 2x od obu stron, dostajemy x - 40 = 0. Dodając 40 do obu stron, dostajemy x = 40. Zatem kąt α ma miarę 40 stopni.

Zastosowania tej wiedzy są bardzo szerokie w geometrii. Często, żeby rozwiązać bardziej skomplikowane zadanie, trzeba najpierw zidentyfikować kąty wpisane i środkowe oparte na tym samym łuku, a następnie wykorzystać tę zasadę, żeby znaleźć brakujące kąty lub boki.

Na przykład, możesz spotkać się z zadaniem, w którym dany jest trójkąt wpisany w okrąg. Wiedząc, że suma kątów w trójkącie wynosi 180 stopni, oraz wykorzystując zasadę o kącie wpisanym i środkowym, możesz obliczyć miary poszczególnych kątów trójkąta.

Inny przykład to zadania z czworokątami wpisanymi w okrąg. Suma przeciwległych kątów w takim czworokącie wynosi 180 stopni. To wynika właśnie z własności kątów wpisanych i środkowych.

Pamiętaj też o szczególnych przypadkach. Kąt wpisany oparty na średnicy okręgu jest zawsze kątem prostym (ma 90 stopni). Wynika to z tego, że kąt środkowy oparty na średnicy ma 180 stopni (jest to kąt półpełny), a kąt wpisany jest dwa razy mniejszy.

Podsumowując:

• Punkt O to środek okręgu.
• Kąt wpisany α ma wierzchołek na okręgu, a ramiona przecinają okrąg.
• Kąt środkowy ma wierzchołek w środku okręgu, a ramiona przecinają okrąg w tych samych punktach, co ramiona kąta wpisanego.
• Kąt środkowy jest dwa razy większy od kąta wpisanego, jeśli oba są oparte na tym samym łuku.

Ćwicz rozwiązywanie zadań, a szybko opanujesz tę zasadę i będziesz mógł z łatwością radzić sobie z bardziej złożonymi problemami z geometrii. Powodzenia!