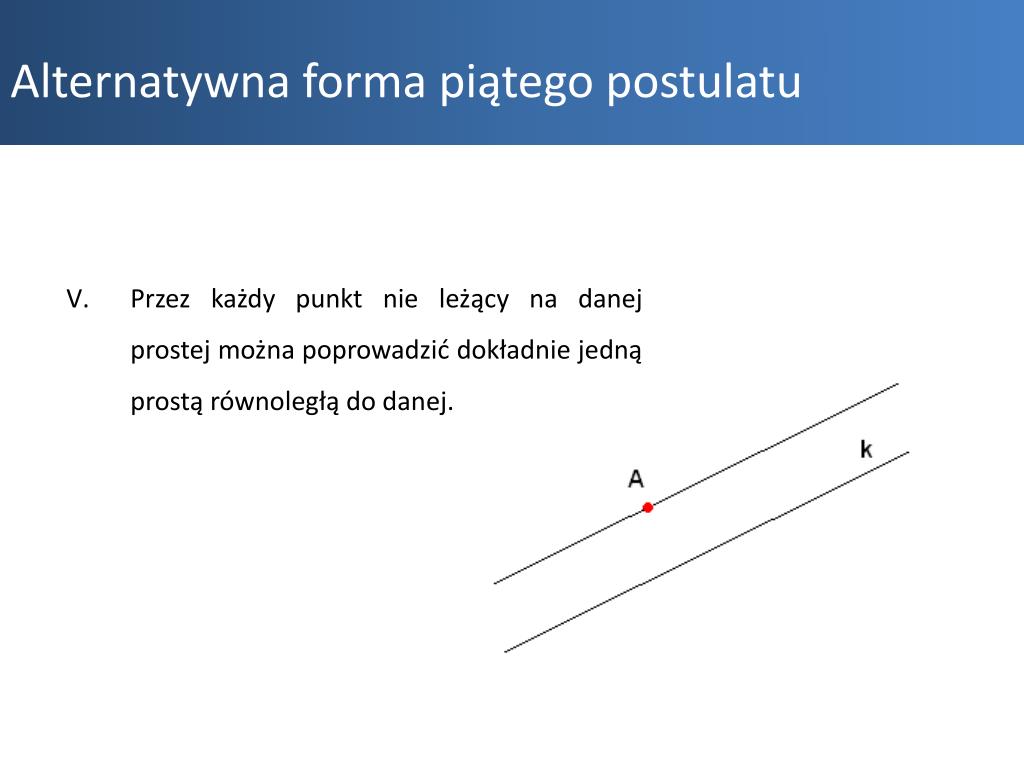
Przez Dowolne Punkty Można Poprowadzić Tylko Jedną Prostą

Dobrze, spróbujmy to wytłumaczyć w prosty sposób.

Wyobraź sobie, że masz kartkę papieru i rysujesz na niej dwa punkty. Dwa kropki, ot tak. Powiedzmy, że jedna kropka jest czerwona, a druga niebieska. Twoim zadaniem jest narysować linię, która przechodzi przez obie te kropki.

Weź linijkę. Przyłóż ją do czerwonej kropki. Teraz delikatnie obracaj linijkę, aż dotknie również niebieskiej kropki. Rysujesz linię. Świetnie! Masz prostą przechodzącą przez dwa punkty.

A teraz pytanie: czy możesz narysować inną linię, która również przechodzi przez te same dwie kropki? Spróbuj. Obracaj linijkę, przesuwaj ją… Zobaczysz, że nie da rady. Za każdym razem, gdy linia będzie przechodzić przez czerwoną i niebieską kropkę, będzie to dokładnie ta sama linia. Możesz ją przedłużyć, skrócić, ale to nadal ta sama prosta.

Co to oznacza?

To oznacza, że przez dwa różne punkty można poprowadzić tylko jedną prostą. To bardzo ważna zasada w geometrii. To tak fundamentalne, jak to, że 1 + 1 = 2.

Pomyśl o tym w ten sposób: dwa punkty wyznaczają jednoznacznie kierunek prostej. Wyobraź sobie, że punkty to dwie wieże. Musisz poprowadzić kabel między nimi. Jest tylko jeden sposób, żeby kabel był idealnie prosty i łączył obie wieże. Każda inna droga będzie albo krótsza (czyli nie będzie prostą), albo dłuższa (czyli też nie będzie prostą).

Jak to działa w praktyce?

Ta zasada jest bardzo przydatna w wielu sytuacjach. Na przykład, jeśli masz jakieś dane, które układasz na wykresie i widzisz, że układają się wzdłuż prostej, to wiesz, że możesz opisać te dane za pomocą prostego równania liniowego.

Inny przykład: geodezja. Geodeci muszą bardzo dokładnie mierzyć odległości i kąty. Często wykorzystują tę zasadę, żeby upewnić się, że ich pomiary są poprawne. Mierzą położenie dwóch punktów, wyznaczają prostą, a potem sprawdzają, czy inne punkty leżą na tej prostej. Jeśli nie, to znaczy, że gdzieś popełnili błąd.

A nawet w życiu codziennym! Kiedy wieszasz obrazek na ścianie, najpierw robisz dwa otwory na gwoździe. Chcesz, żeby obrazek wisiał prosto, więc używasz linijki (albo poziomicy) żeby upewnić się, że otwory są w jednej linii. Innymi słowy, chcesz, żeby gwoździe leżały na jednej prostej. I znowu, korzystasz z zasady, że przez dwa punkty przechodzi tylko jedna prosta.

Dlaczego to takie ważne?

Bo to pozwala nam budować spójny i logiczny system geometrii. Dzięki tej zasadzie możemy definiować inne pojęcia, takie jak odcinki, półproste, kąty, i tak dalej. Bez tej zasady geometria byłaby chaotyczna i trudna do zrozumienia.

Wyobraź sobie, że nie można jednoznacznie narysować prostej przez dwa punkty. Wtedy rysowanie planów budynków, projektowanie mostów, albo nawet granie w bilard byłoby bardzo trudne! Wszystko opiera się na tym, że proste są "proste" i że zachowują się w przewidywalny sposób.

A co, gdybyśmy mieli trzy punkty? Czy zawsze można poprowadzić prostą przez trzy punkty? Niekoniecznie! Jeśli te trzy punkty leżą na jednej prostej (mówimy, że są współliniowe), to tak, można. Ale jeśli nie leżą na jednej prostej, to nie da się. Spróbuj narysować trzy kropki na kartce, tak żeby nie dało się narysować prostej, która by przechodziła przez wszystkie trzy. Zobaczysz, że zawsze tworzą one wierzchołki trójkąta.

Dlatego właśnie zasada, że przez dwa punkty przechodzi tylko jedna prosta, jest tak podstawowa. To fundament, na którym buduje się całą geometrię. To jak alfabet, którym piszemy język geometrii.

Podsumowując:

Masz dwa punkty.
Możesz narysować prostą, która przechodzi przez oba punkty.
Nie możesz narysować innej prostej, która również przechodzi przez oba punkty.
Dlatego przez dwa punkty przechodzi tylko jedna prosta.

I to wszystko! Mam nadzieję, że to wyjaśnienie jest jasne i zrozumiałe. Geometria może wydawać się trudna na początku, ale tak naprawdę to tylko zestaw prostych zasad, które, kiedy już się je zrozumie, otwierają drzwi do fascynującego świata kształtów i przestrzeni. Pamiętaj, rysuj dużo i eksperymentuj! To najlepszy sposób, żeby nauczyć się geometrii.