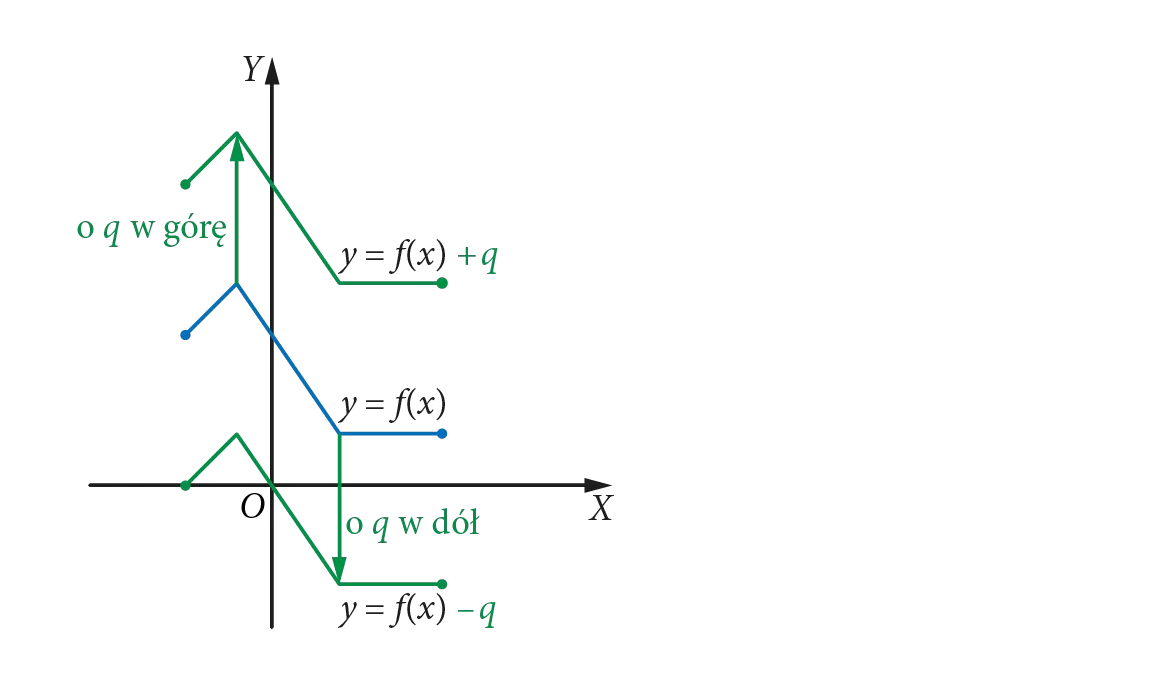Przesuwanie Wzdłuż Osi Ox I Oy

W matematyce, a w szczególności w geometrii analitycznej, transformacje przestrzeni odgrywają fundamentalną rolę. Jedną z najprostszych i zarazem najczęściej wykorzystywanych transformacji jest przesuwanie (translacja) wzdłuż osi Ox i Oy. Zrozumienie tego zagadnienia jest kluczowe dla wielu dziedzin, od grafiki komputerowej po fizykę i inżynierię.

Podstawy Przesuwania

Przesuwanie, nazywane również translacją, to transformacja, która przesuwa każdy punkt w przestrzeni o stałą odległość w określonym kierunku. W kontekście dwuwymiarowym, czyli na płaszczyźnie kartezjańskiej, przesunięcie można opisać jako wektor (a, b), gdzie a reprezentuje przesunięcie wzdłuż osi Ox (osi poziomej), a b reprezentuje przesunięcie wzdłuż osi Oy (osi pionowej).

Równania Translacji

Matematycznie, przesunięcie punktu P(x, y) o wektor (a, b) prowadzi do nowego punktu P'(x', y'), gdzie:

x' = x + a

y' = y + b

Innymi słowy, współrzędna x nowego punktu P' jest sumą współrzędnej x punktu P i wartości a (przesunięcia wzdłuż osi Ox). Analogicznie, współrzędna y nowego punktu P' jest sumą współrzędnej y punktu P i wartości b (przesunięcia wzdłuż osi Oy).

Przesuwanie Kształtów i Funkcji

Przesuwanie nie ogranicza się tylko do pojedynczych punktów. Możemy również przesuwać całe kształty geometryczne lub wykresy funkcji. W takim przypadku, przesuwamy każdy punkt należący do danego kształtu lub wykresu o ten sam wektor (a, b).

Przesuwanie Funkcji

Jeśli mamy funkcję f(x), to przesunięcie jej wykresu o wektor (a, b) daje nam nową funkcję g(x), zdefiniowaną jako:

g(x) = f(x - a) + b

Zauważmy, że przesunięcie wzdłuż osi Ox (o wartość a) wpływa na argument funkcji (x - a), natomiast przesunięcie wzdłuż osi Oy (o wartość b) dodaje się do wartości funkcji.

Przykłady Przesuwania Funkcji

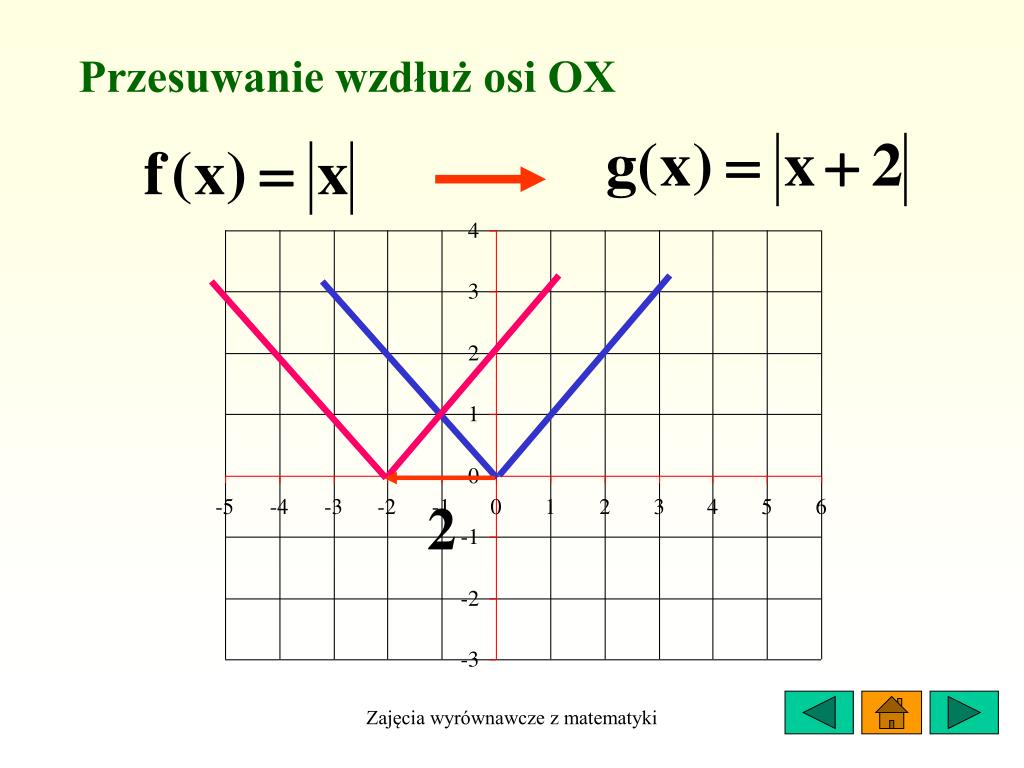
Przesunięcie funkcji liniowej: Jeśli mamy funkcję f(x) = x, to przesunięcie jej o wektor (2, 3) daje nam funkcję g(x) = (x - 2) + 3 = x + 1.
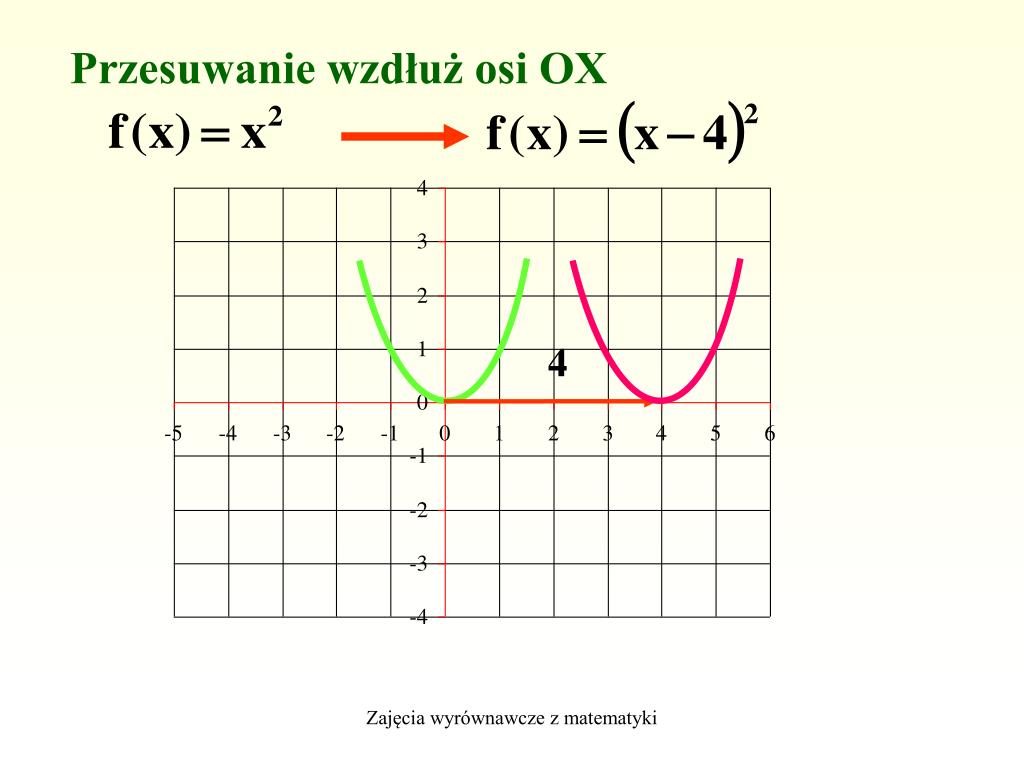
Przesunięcie funkcji kwadratowej: Jeśli mamy funkcję f(x) = x², to przesunięcie jej o wektor (-1, 2) daje nam funkcję g(x) = (x + 1)² + 2.

Zastosowania Przesuwania

Przesuwanie ma szerokie zastosowanie w wielu dziedzinach nauki i techniki. Oto kilka przykładów:

Grafika Komputerowa

W grafice komputerowej, przesuwanie jest fundamentalną operacją. Umożliwia ono przesuwanie obiektów na ekranie, tworzenie animacji, a także manipulowanie kamerą w wirtualnym świecie. Na przykład, w grach wideo, przesunięcie jest używane do przesuwania postaci gracza, elementów otoczenia i innych obiektów.

Fizyka

W fizyce, przesunięcie jest używane do opisywania ruchu ciał. Na przykład, jeśli znamy położenie ciała w pewnym momencie czasu, to możemy obliczyć jego położenie w innym momencie czasu, jeśli znamy jego prędkość i czas, jaki upłynął. Możemy to zrobić, przesuwając początkowe położenie ciała o wektor prędkości pomnożony przez czas.

Inżynieria

W inżynierii, przesunięcie jest używane w wielu różnych zastosowaniach, takich jak projektowanie mostów, budynków i innych konstrukcji. Na przykład, podczas projektowania mostu, inżynierowie muszą uwzględnić przesunięcia spowodowane obciążeniem mostu. Muszą również uwzględnić przesunięcia spowodowane zmianami temperatury.

Przetwarzanie Obrazów

W przetwarzaniu obrazów, translacja może służyć do wyrównywania obrazów, kompensowania ruchów kamery lub do tworzenia efektów specjalnych. Na przykład, można przesunąć obraz tak, aby określony obiekt w obrazie znajdował się w centrum.

Dane Geograficzne

W systemach informacji geograficznej (GIS), przesunięcie jest używane do przekształcania współrzędnych geograficznych. Na przykład, można przesunąć współrzędne tak, aby dany obszar znajdował się w innym układzie współrzędnych.

Przesuwanie a Inne Transformacje

Przesuwanie jest jedną z wielu transformacji, które można zastosować do obiektów w przestrzeni. Inne popularne transformacje to:

Skalowanie: Zmiana rozmiaru obiektu.
Obrót: Obrócenie obiektu wokół określonego punktu.
Ścinanie: Przekształcenie, które zmienia kształt obiektu, zachowując jego pole.
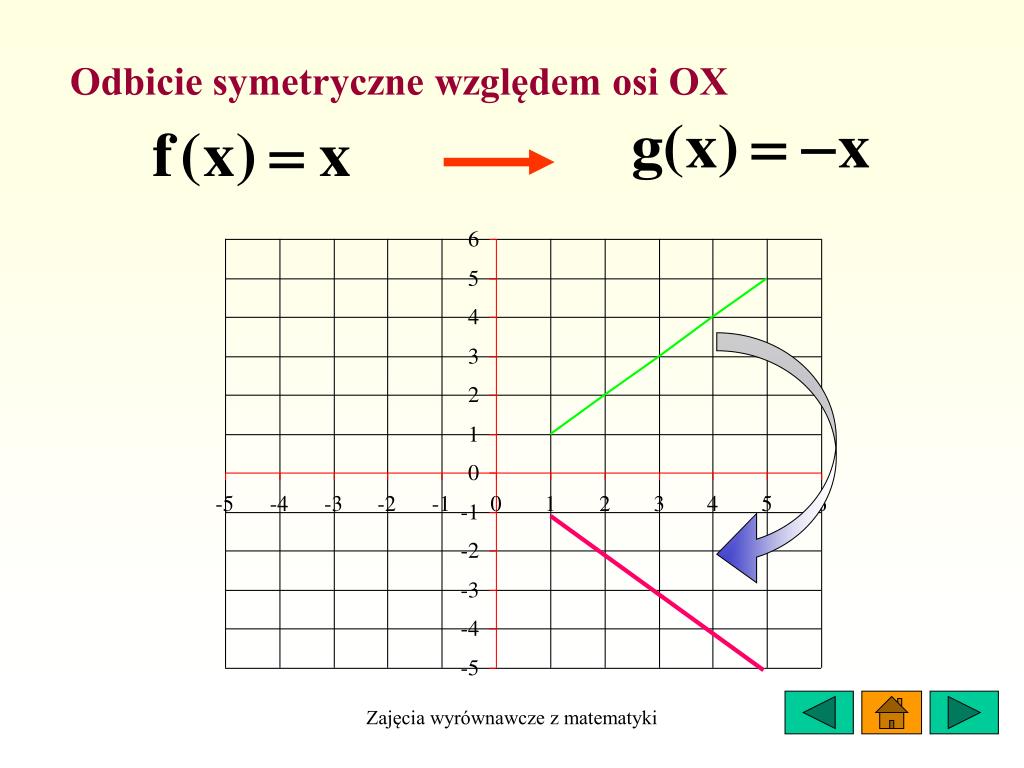
Odbicie: Odbicie obiektu względem osi lub punktu.

Wszystkie te transformacje można łączyć ze sobą, tworząc bardziej złożone transformacje. Na przykład, można przesunąć obiekt, a następnie go obrócić.

Praktyczne Przykłady z Danymi

Wyobraźmy sobie, że mamy mapę miasta i chcemy przesunąć ją tak, aby punkt o współrzędnych (0,0) w naszym układzie odniesienia odpowiadał centrum miasta, które ma rzeczywiste współrzędne geograficzne (52.23, 21.01) - Warszawa. W takim przypadku, a = 52.23 i b = 21.01. Każdy punkt na mapie (x, y) musimy przesunąć o wektor (52.23, 21.01), aby uzyskać jego rzeczywiste położenie geograficzne.

Inny przykład, w robotyce. Robot ma zaprogramowaną ścieżkę ruchu względem swojego układu współrzędnych. Aby robot mógł poruszać się po pomieszczeniu, którego układ współrzędnych różni się od układu robota, konieczne jest przesunięcie całej ścieżki o wektor, który reprezentuje różnicę między tymi układami.

Podsumowanie i Wnioski

Przesuwanie, choć proste w swojej koncepcji, jest niezwykle potężnym narzędziem w matematyce i w wielu innych dziedzinach. Pozwala ono na łatwe przesuwanie obiektów w przestrzeni, co znajduje zastosowanie w grafice komputerowej, fizyce, inżynierii i wielu innych dziedzinach. Zrozumienie podstaw przesuwania jest kluczowe dla każdego, kto zajmuje się modelowaniem geometrycznym, analizą danych przestrzennych lub programowaniem grafiki. Pamiętaj, że kluczem do opanowania tego zagadnienia jest praktyka! Wypróbuj samodzielnie przesuwanie różnych kształtów i funkcji, aby lepiej zrozumieć, jak działa ta transformacja.

Zachęcam do dalszego zgłębiania wiedzy na temat transformacji geometrycznych. Poznanie bardziej zaawansowanych transformacji, takich jak obroty, skalowanie i ścinanie, pozwoli Ci na tworzenie bardziej złożonych i realistycznych modeli i symulacji.