Przesunięcie Wykresu Funkcji Kwadratowej Wzdłuż Osi Ox I Oy

Przesuwanie wykresów funkcji kwadratowych wzdłuż osi OX i OY to fundament zrozumienia transformacji funkcji w matematyce. Zmiana położenia paraboli na układzie współrzędnych pozwala na modelowanie różnych zjawisk fizycznych i ekonomicznych, a także upraszcza rozwiązywanie problemów optymalizacyjnych. Rozważmy zatem, jak modyfikować wzór funkcji kwadratowej, aby uzyskać przesunięcie jej wykresu.

Funkcja kwadratowa w postaci ogólnej wyraża się wzorem:

f(x) = ax² + bx + c

gdzie a, b i c są stałymi, a a ≠ 0. Wykres tej funkcji to parabola. Wartość a decyduje o kierunku otwarcia ramion paraboli (do góry, gdy a > 0, do dołu, gdy a < 0) oraz o jej "szerokości". Zmiany b i c wpływają na położenie wierzchołka paraboli. Alternatywną, często bardziej użyteczną postacią, jest postać kanoniczna:

f(x) = a(x - p)² + q

gdzie (p, q) to współrzędne wierzchołka paraboli. Przekształcenie funkcji do postaci kanonicznej ułatwia identyfikację wierzchołka i upraszcza proces przesuwania wykresu. Przejście z postaci ogólnej do kanonicznej można zrealizować poprzez dopełnienie do kwadratu.

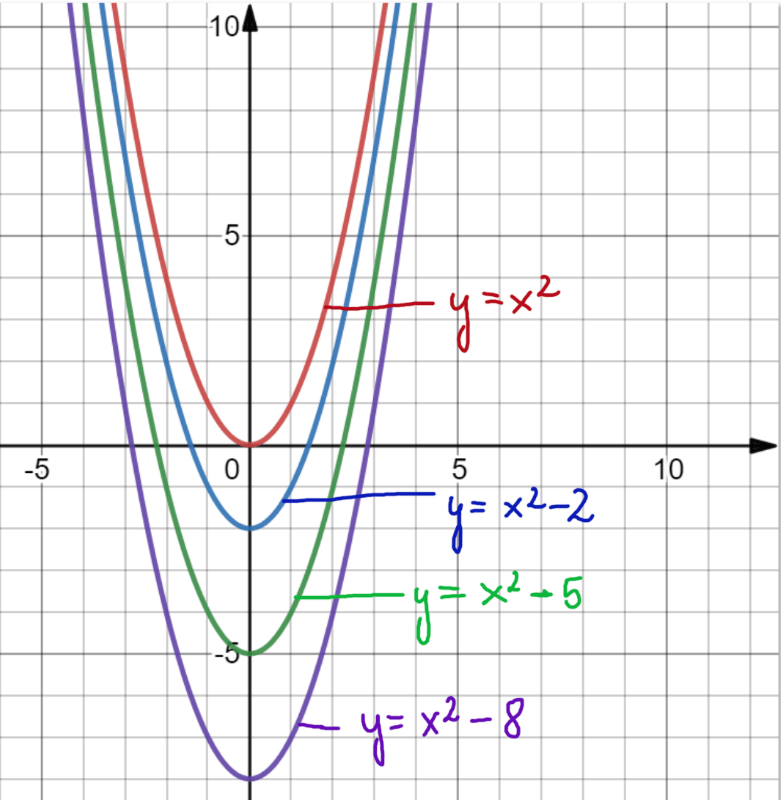
Przesunięcie wzdłuż osi OY (pionowe)

Rozpocznijmy od najprostszego przypadku: przesunięcia wykresu funkcji kwadratowej wzdłuż osi OY. Aby przesunąć wykres funkcji f(x) o k jednostek w górę, dodajemy k do wartości funkcji:

g(x) = f(x) + k

Jeśli k > 0, parabola przesuwa się w górę. Jeśli k < 0, parabola przesuwa się w dół. Na przykład, mając funkcję f(x) = x², przesunięcie o 3 jednostki w górę daje nam funkcję g(x) = x² + 3. Wierzchołek paraboli f(x) = x², który znajduje się w punkcie (0, 0), po przesunięciu znajdzie się w punkcie (0, 3). Podobnie, przesunięcie o -2 jednostki (czyli w dół) dałoby funkcję h(x) = x² - 2, z wierzchołkiem w (0, -2).

Rozważmy bardziej złożony przykład. Niech f(x) = 2(x - 1)² + 4. Jej wierzchołek znajduje się w punkcie (1, 4). Przesunięcie tej funkcji o 5 jednostek w dół, czyli o k = -5, da nam funkcję:

g(x) = 2(x - 1)² + 4 - 5 = 2(x - 1)² - 1

Wierzchołek nowej paraboli znajduje się teraz w punkcie (1, -1). Zauważmy, że zmiana dotyczy jedynie współrzędnej q w postaci kanonicznej – przesunięcie wzdłuż osi OY nie wpływa na współrzędną p.

Przesunięcie wzdłuż osi OY jest addytywną transformacją funkcji. Dodajemy stałą wartość do całej funkcji, co powoduje translację wykresu w pionie. Wartość dodawana (lub odejmowana) bezpośrednio determinuje wielkość i kierunek przesunięcia.

Przesunięcie wzdłuż osi OX (poziome)

Przesunięcie wykresu funkcji kwadratowej wzdłuż osi OX, czyli poziome, wymaga subtelniejszej operacji. Aby przesunąć wykres funkcji f(x) o p jednostek w prawo, zastępujemy x przez (x - p) w całym wzorze funkcji:

g(x) = f(x - p)

Jeśli p > 0, parabola przesuwa się w prawo. Jeśli p < 0, parabola przesuwa się w lewo. Kluczowe jest zrozumienie, że p we wzorze f(x - p) reprezentuje przesunięcie w prawo. Dlatego, aby przesunąć wykres w lewo, musimy dodać wartość do x (czyli p będzie ujemne).

Powróćmy do prostego przykładu f(x) = x². Przesunięcie o 2 jednostki w prawo daje nam funkcję g(x) = (x - 2)². Wierzchołek paraboli przesunął się z punktu (0, 0) do punktu (2, 0). Zauważ, że przesunięcie poziome wpływa na wartość wewnątrz nawiasu kwadratowego.

A co, jeśli chcemy przesunąć wykres w lewo? Powiedzmy, że o 4 jednostki. Wtedy p = -4, a nowa funkcja to:

h(x) = (x - (-4))² = (x + 4)²

Wierzchołek paraboli przesunął się do punktu (-4, 0).

Ponownie, spójrzmy na bardziej złożony przykład: f(x) = 2(x - 1)² + 4. Chcemy przesunąć tę funkcję o 3 jednostki w lewo. Oznacza to, że p = -3. Zatem:

g(x) = 2((x - (-3)) - 1)² + 4 = 2(x + 3 - 1)² + 4 = 2(x + 2)² + 4

Wierzchołek paraboli f(x) znajdował się w punkcie (1, 4). Wierzchołek paraboli g(x) znajduje się w punkcie (-2, 4). Zauważmy, że przesunięcie wzdłuż osi OX wpłynęło na współrzędną p w postaci kanonicznej, a współrzędna q pozostała niezmieniona.

Przesunięcie wzdłuż osi OX jest transformacją, która modyfikuje argument funkcji. Zamiast obliczać wartość funkcji dla x, obliczamy ją dla x - p. To subtelna, ale fundamentalna różnica, która prowadzi do przesunięcia wykresu w poziomie. Pamiętajmy o zmianie znaku przy podstawianiu wartości p – przesunięcie w prawo oznacza odejmowanie od x, a przesunięcie w lewo oznacza dodawanie do x.

Podsumowując, przesunięcie wykresu funkcji kwadratowej wzdłuż osi OX i OY to proces, który pozwala na elastyczne modelowanie i analizę różnych zjawisk. Przesunięcie wzdłuż osi OY polega na dodaniu stałej wartości do całej funkcji, co przesuwa wykres w górę lub w dół. Przesunięcie wzdłuż osi OX polega na zastąpieniu x przez (x - p), co przesuwa wykres w prawo lub w lewo. Zrozumienie tych transformacji jest kluczowe do pełnego opanowania własności funkcji kwadratowych i ich zastosowań.