Przekątna Graniastosłupa Prawidłowego Czworokątnego Ma Długość D

Okej, spróbujmy wyjaśnić kwestię przekątnej graniastosłupa prawidłowego czworokątnego.

Zacznijmy od początku. Graniastosłup prawidłowy czworokątny – co to w ogóle jest? Wyobraź sobie pudełko. Ale takie specjalne pudełko. Jego podstawa to kwadrat – idealny, wszystkie boki równe. No i ten kwadrat to dół i góra naszego pudełka. Ściany boczne są prostokątami. To właśnie jest graniastosłup prawidłowy czworokątny. "Prawidłowy" oznacza, że podstawa jest regularnym wielokątem (w tym wypadku kwadratem), a "czworokątny" – że podstawa ma cztery boki.

Teraz ta nieszczęsna przekątna. Mówimy o przekątnej całego graniastosłupa, a nie tylko podstawy. Wyobraź sobie linię, która biegnie od jednego wierzchołka dolnej podstawy do wierzchołka górnej podstawy, ale PO PRZEKĄTNEJ, czyli nie po krawędzi. Ta linia przechodzi przez wnętrze graniastosłupa. I to właśnie ta linia ma długość D. My chcemy dowiedzieć się, jak ta długość D zależy od innych wymiarów naszego graniastosłupa.

Żeby to zrozumieć, potrzebujemy trochę geometrii i twierdzenia Pitagorasa.

Krok po kroku do celu

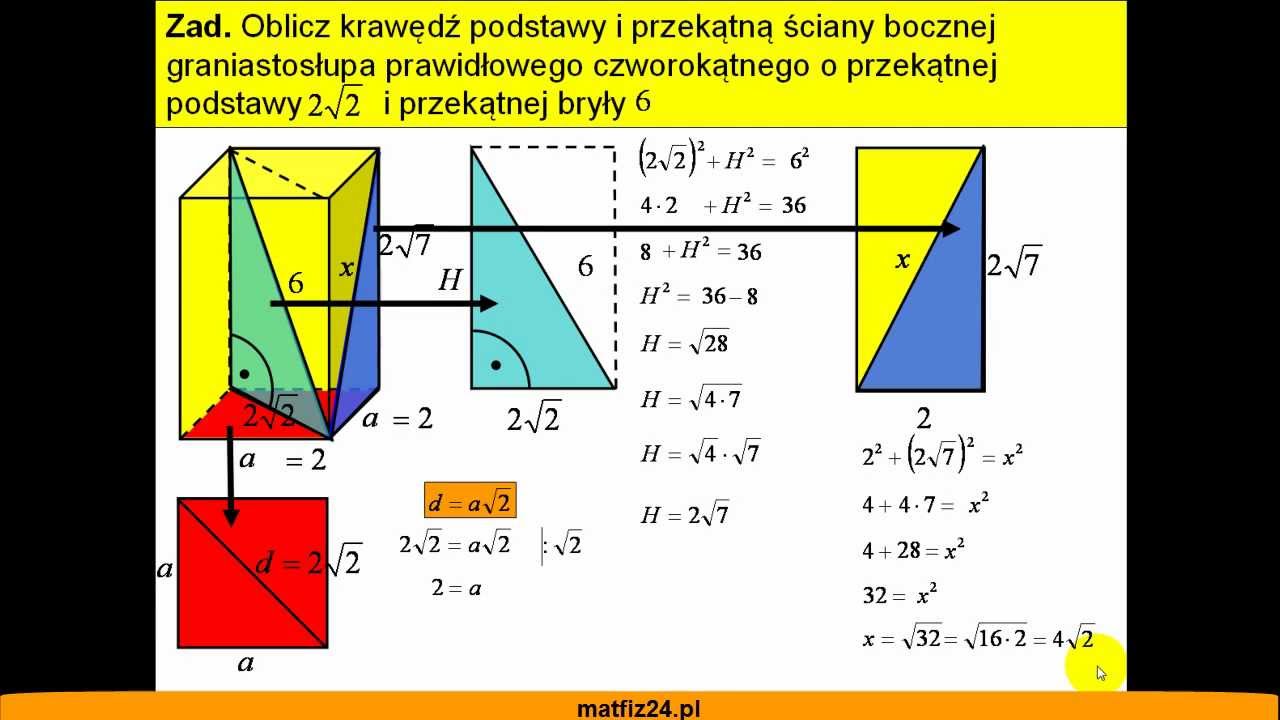
Mamy nasz graniastosłup. Oznaczmy długość boku kwadratu w podstawie jako a. Oznaczmy wysokość graniastosłupa jako h. Nasza przekątna graniastosłupa ma długość D. Musimy znaleźć związek między a, h i D.

Najpierw spójrzmy na podstawę, czyli kwadrat. Ma on przekątną. Oznaczmy długość tej przekątnej podstawy jako p. Możemy ją obliczyć używając twierdzenia Pitagorasa dla trójkąta prostokątnego utworzonego przez dwa boki kwadratu i jego przekątną. Czyli: p² = a² + a², a to się równa p² = 2a². Zatem p = √(2a²), a to jest to samo co p = a√2. Czyli przekątna kwadratu to a√2. Zapamiętajmy to.

Teraz wyobraź sobie trójkąt prostokątny wewnątrz graniastosłupa. Jedna przyprostokątna to przekątna podstawy (p), druga przyprostokątna to wysokość graniastosłupa (h), a przeciwprostokątna to nasza szukana przekątna graniastosłupa (D). Znowu używamy twierdzenia Pitagorasa!

Mamy: D² = p² + h². Ale wiemy, że p = a√2, więc p² = (a√2)² = 2a².

Wstawiamy to do naszego równania: D² = 2a² + h².

Teraz możemy wyciągnąć pierwiastek kwadratowy z obu stron, żeby otrzymać D: D = √(2a² + h²).

Więc mamy wzór na przekątną graniastosłupa prawidłowego czworokątnego: D = √(2a² + h²), gdzie a to długość boku podstawy (kwadratu), a h to wysokość graniastosłupa.

Użyteczne wnioski

Ten wzór pokazuje, że długość przekątnej graniastosłupa zależy bezpośrednio od długości boku podstawy i wysokości graniastosłupa. Im większy bok podstawy i im wyższy graniastosłup, tym dłuższa przekątna.

Co jeśli znamy długość przekątnej D i chcemy obliczyć np. wysokość h, znając długość boku podstawy a? Wystarczy przekształcić nasz wzór.

Zaczynamy od D = √(2a² + h²). Podnosimy obie strony do kwadratu: D² = 2a² + h².

Teraz chcemy wyizolować h², więc odejmujemy 2a² od obu stron: D² - 2a² = h².

Na koniec wyciągamy pierwiastek kwadratowy z obu stron: h = √(D² - 2a²).

Analogicznie, jeśli znamy D i h, a chcemy obliczyć a, postępujemy podobnie:

D² = 2a² + h² D² - h² = 2a² (D² - h²) / 2 = a² a = √((D² - h²) / 2)

Pamiętaj, że to, co jest pod pierwiastkiem, musi być liczbą nieujemną. Oznacza to, że D² musi być większe lub równe 2a² (w przypadku obliczania h) oraz D² musi być większe lub równe h² (w przypadku obliczania a). Inaczej nie ma rozwiązania w liczbach rzeczywistych. Wynika to z geometrii – przekątna musi być dłuższa niż inne wymiary.

Podsumowanie i praktyczne zastosowanie

Wzór D = √(2a² + h²) jest bardzo użyteczny. Wyobraź sobie, że projektujesz jakieś pudełka i musisz zapewnić, że zmieszczą się one w paczce o określonej przekątnej. Znając wymiary pudełka (bok podstawy a i wysokość h), możesz łatwo obliczyć przekątną i sprawdzić, czy się zmieszczą. Albo, jeśli masz paczkę o danej przekątnej i chcesz w niej umieścić jak największe pudełka, możesz użyć przekształconych wzorów, żeby znaleźć maksymalne wymiary pudełka, które się zmieści.

Pamiętaj, że cały czas mówimy o graniastosłupie prawidłowym czworokątnym. Jeśli podstawa nie jest kwadratem, tylko np. prostokątem, to wzór będzie inny i trzeba będzie użyć innej metody obliczeń, uwzględniającej dwa różne boki prostokąta w podstawie. Wtedy przekątną podstawy obliczamy z twierdzenia Pitagorasa: p² = a² + b², gdzie a i b to boki prostokąta. A następnie stosujemy twierdzenie Pitagorasa dla trójkąta prostokątnego z przekątną podstawy, wysokością i przekątną graniastosłupa.

Mam nadzieję, że to wyjaśnienie jest zrozumiałe. Ćwiczenia z różnymi przykładami pomogą Ci utrwalić tę wiedzę. Powodzenia!