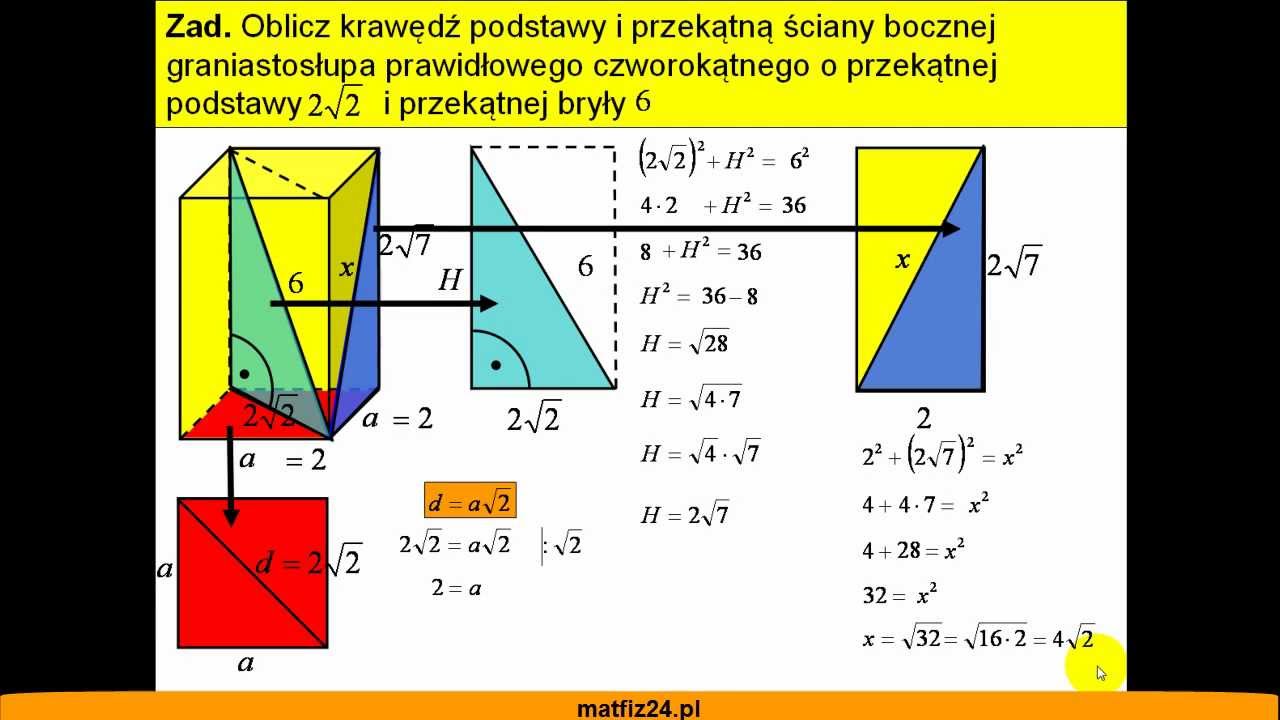
Przekątna Graniastosłupa Prawidłowego Czworokątnego Ma Długość 26 Cm I Tworzy

Dobrze, posłuchajcie uważnie, bo to jest kluczowe. Przekątna graniastosłupa prawidłowego czworokątnego o długości 26 cm i tworząca kąt z płaszczyzną podstawy… No właśnie, ile wynosi ten kąt? Od tego zależy całe rozwiązanie. Załóżmy, że ten kąt, oznaczmy go jako α, jest nam znany. Bez jego wartości nie jesteśmy w stanie jednoznacznie określić wymiarów graniastosłupa.

Zacznijmy od podstawowych definicji. Graniastosłup prawidłowy czworokątny to inaczej prostopadłościan o podstawie będącej kwadratem. Oznacza to, że wszystkie jego ściany boczne są prostokątami, a krawędzie boczne są prostopadłe do podstawy. Długość przekątnej graniastosłupa, oznaczmy ją jako d, wynosi 26 cm. Ta przekątna tworzy kąt α z płaszczyzną podstawy.

Teraz przejdźmy do analizy geometrycznej. Wyobraźmy sobie trójkąt prostokątny, którego przeciwprostokątną jest przekątna graniastosłupa d. Jedną z przyprostokątnych jest przekątna podstawy (kwadratu), oznaczmy ją jako p, a drugą przyprostokątną jest wysokość graniastosłupa, oznaczmy ją jako H.

Z twierdzenia Pitagorasa wynika, że d² = p² + H². Wiemy, że d = 26 cm, więc 26² = p² + H², czyli 676 = p² + H².

Kluczowe jest teraz powiązanie kąta α z naszymi zmiennymi. Z definicji funkcji trygonometrycznych w trójkącie prostokątnym wynika, że sin(α) = H / d oraz cos(α) = p / d. Zatem H = d * sin(α) oraz p = d * cos(α).

Podstawiając to do naszego równania Pitagorasa, otrzymujemy:

676 = (d * cos(α))² + (d * sin(α))² 676 = d² * cos²(α) + d² * sin²(α) 676 = d² * (cos²(α) + sin²(α))

Wiemy, że cos²(α) + sin²(α) = 1, więc 676 = d², co potwierdza, że wszystko robimy poprawnie, ponieważ d = 26 cm.

Teraz musimy znaleźć zależność między przekątną podstawy p a bokiem podstawy a. Podstawa jest kwadratem, więc jej przekątna wynosi p = a√2. Zatem a = p / √2.

Wyraźmy teraz bok podstawy a i wysokość H za pomocą kąta α:

p = d * cos(α) = 26 * cos(α) a = p / √2 = (26 * cos(α)) / √2 = 13√2 * cos(α) H = d * sin(α) = 26 * sin(α)

Mając a i H, możemy obliczyć pole podstawy Pp i objętość V graniastosłupa:

Pp = a² = (13√2 * cos(α))² = 338 * cos²(α) V = Pp * H = 338 * cos²(α) * 26 * sin(α) = 8788 * cos²(α) * sin(α)

Zauważ, że wszystko zależy od wartości kąta α. Bez jego znajomości nie możemy jednoznacznie wyznaczyć wymiarów graniastosłupa, pola podstawy ani jego objętości.

H2 Wpływ Kąta Nachylenia na Wymiary Graniastosłupa

Przyjrzyjmy się teraz, jak różne wartości kąta α wpływają na wymiary naszego graniastosłupa.

• α bliskie 0 stopni: Wtedy sin(α) jest bliskie 0, a cos(α) jest bliskie 1. Oznacza to, że wysokość H jest bardzo mała, a przekątna podstawy p jest bliska długości przekątnej graniastosłupa d, czyli 26 cm. W konsekwencji bok podstawy a jest bliski 26 / √2 = 13√2 cm. Graniastosłup jest bardzo "płaski", przypominający cienki plaster. Objętość V jest bliska zeru.
• α bliskie 90 stopni: Wtedy sin(α) jest bliskie 1, a cos(α) jest bliskie 0. Oznacza to, że wysokość H jest bliska długości przekątnej graniastosłupa d, czyli 26 cm, a przekątna podstawy p jest bardzo mała. W konsekwencji bok podstawy a jest bardzo mały. Graniastosłup jest bardzo "wysoki" i "chudy". Pole podstawy Pp jest bliskie zeru, a objętość V również jest bliska zeru.
• α = 45 stopni: Wtedy sin(α) = cos(α) = √2 / 2. Oznacza to, że H = 26 * (√2 / 2) = 13√2 cm oraz p = 26 * (√2 / 2) = 13√2 cm. Wtedy a = p / √2 = (13√2) / √2 = 13 cm. Objętość wynosi V = 8788 * (√2/2)² * (√2/2) = 8788 * (1/2) * (√2/2) = 4394 * (√2/2) = 2197√2 cm³.

Widzimy, że w zależności od kąta α, kształt graniastosłupa zmienia się diametralnie, wpływając na jego wymiary i objętość.

H2 Określenie Wymiarów na Podstawie Dodatkowych Informacji

Załóżmy, że oprócz długości przekątnej d = 26 cm znamy również wysokość graniastosłupa H. Na przykład, niech H = 10 cm. Wtedy możemy obliczyć kąt α:

sin(α) = H / d = 10 / 26 = 5/13 α = arcsin(5/13) ≈ 22.62 stopnia

Teraz możemy obliczyć przekątną podstawy p:

p = d * cos(α) = 26 * cos(arcsin(5/13))

Aby uprościć to wyrażenie, zauważmy, że cos(arcsin(x)) = √(1 - x²). Zatem:

p = 26 * √(1 - (5/13)²) = 26 * √(1 - 25/169) = 26 * √(144/169) = 26 * (12/13) = 24 cm

Teraz możemy obliczyć bok podstawy a:

a = p / √2 = 24 / √2 = 12√2 cm

Pole podstawy wynosi:

Pp = a² = (12√2)² = 288 cm²

A objętość graniastosłupa:

V = Pp * H = 288 * 10 = 2880 cm³

Zatem, mając dodatkową informację, taką jak wysokość, jesteśmy w stanie jednoznacznie określić wszystkie wymiary graniastosłupa.

H2 Przypadek Szczególny: Sześcian

Jeśli nasz graniastosłup prawidłowy czworokątny jest sześcianem, to wszystkie jego krawędzie są równe, czyli a = H. Wtedy przekątna graniastosłupa d wyraża się wzorem d = a√3.

W naszym przypadku d = 26 cm, więc a√3 = 26. Zatem a = 26 / √3 = (26√3) / 3 cm.

W tym przypadku, kąt α, jaki przekątna tworzy z płaszczyzną podstawy, można obliczyć jako:

tan(α) = H / p = a / (a√2) = 1 / √2 α = arctan(1 / √2) ≈ 35.26 stopnia

Zatem, w przypadku sześcianu, wszystko jest jednoznacznie określone przez długość przekątnej.

Podsumowując, kluczowym elementem w rozwiązaniu tego zadania jest znajomość kąta, jaki przekątna graniastosłupa tworzy z płaszczyzną podstawy, lub innej dodatkowej informacji, takiej jak wysokość graniastosłupa. Bez tej informacji nie jesteśmy w stanie jednoznacznie określić wymiarów graniastosłupa. Pamiętajcie o twierdzeniu Pitagorasa i definicjach funkcji trygonometrycznych. To są podstawowe narzędzia w rozwiązywaniu tego typu problemów.