Prostokąty I Kwadraty Klasa 5

Witaj w fascynującym świecie prostokątów i kwadratów! Ten artykuł jest przeznaczony dla uczniów klasy 5 i ma na celu wprowadzenie oraz pogłębienie wiedzy na temat tych podstawowych figur geometrycznych. Przygotuj się na podróż, podczas której odkryjemy ich właściwości, nauczymy się obliczać ich obwody i pola, a także zobaczymy, jak te figury geometryczne otaczają nas w życiu codziennym.

Co to jest Prostokąt i Kwadrat?

Definicje i podstawowe cechy

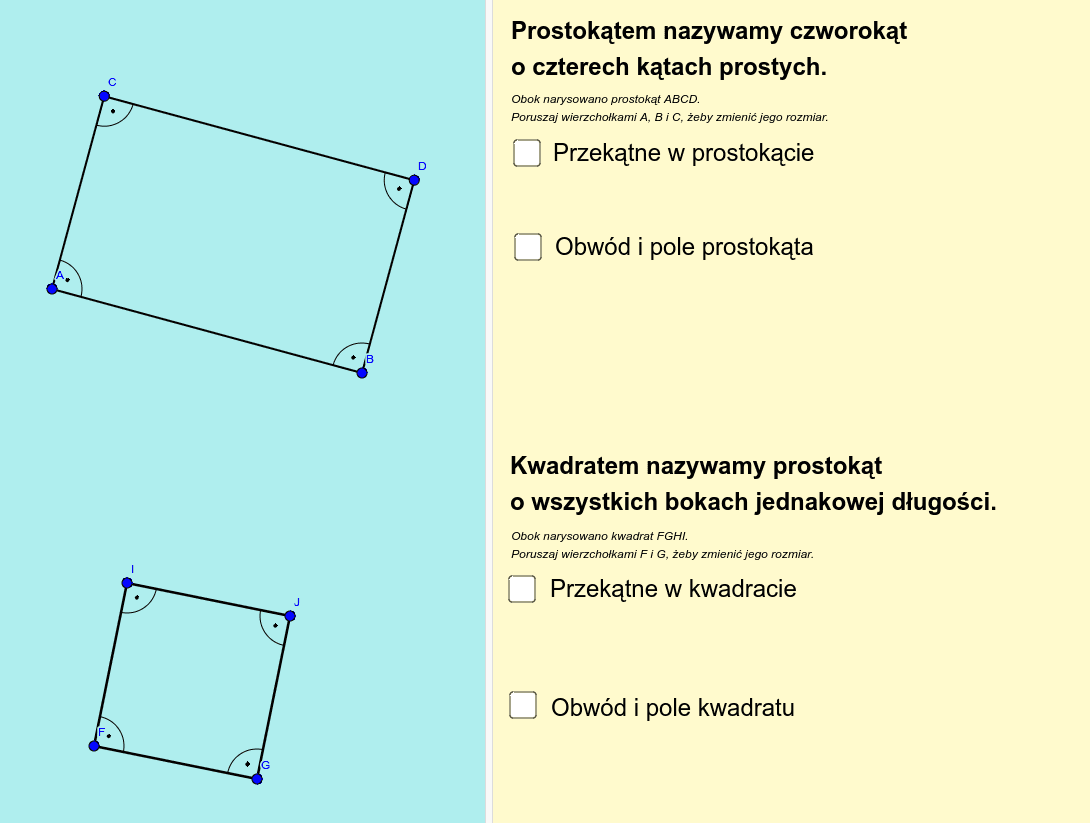
Prostokąt to czworokąt, który ma cztery kąty proste. Oznacza to, że każdy z jego kątów ma miarę 90 stopni. Prostokąt ma dwa boki krótsze (zwane szerokością) i dwa boki dłuższe (zwane długością). Przeciwległe boki prostokąta są równe i równoległe.

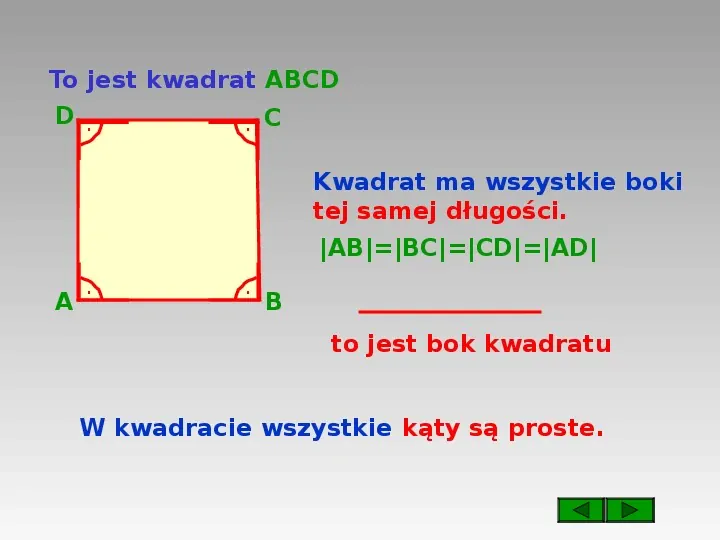
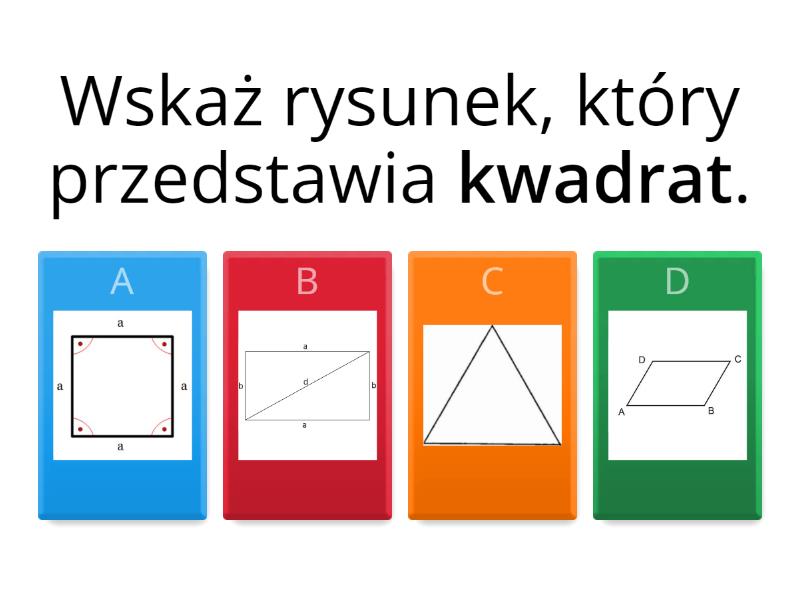
Kwadrat to szczególny przypadek prostokąta. To czworokąt, który ma cztery kąty proste i wszystkie cztery boki równe. Oznacza to, że kwadrat jest jednocześnie prostokątem, ale nie każdy prostokąt jest kwadratem.

Zapamiętaj! Kwadrat musi mieć wszystkie boki tej samej długości, a prostokąt musi mieć tylko kąty proste. Ważne jest, aby rozróżniać te figury.

Różnice i Podobieństwa

Podobieństwa: Oba, prostokąt i kwadrat, są czworokątami. Oba mają cztery kąty proste (90 stopni). Przeciwległe boki w prostokącie są równoległe, a w kwadracie wszystkie boki są parami równoległe.

Różnice: Kwadrat ma wszystkie boki równe, a prostokąt ma tylko przeciwległe boki równe. Kwadrat jest "bardziej symetryczny" niż prostokąt, ponieważ można go obrócić o 90 stopni i nadal wygląda tak samo.

Obwód Prostokąta i Kwadratu

Obliczanie Obwodu Prostokąta

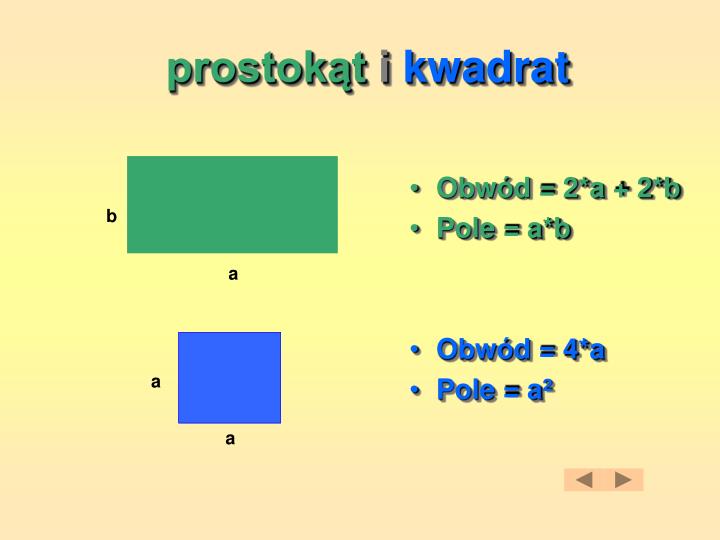
Obwód to suma długości wszystkich boków figury. Aby obliczyć obwód prostokąta, musimy dodać długości wszystkich jego boków. Jeśli długość prostokąta oznaczymy jako a, a szerokość jako b, to wzór na obwód prostokąta wygląda następująco:

Obwód prostokąta = 2 * a + 2 * b lub Obwód prostokąta = 2 * (a + b)

Przykład: Prostokąt ma długość 5 cm i szerokość 3 cm. Jego obwód to 2 * 5 cm + 2 * 3 cm = 10 cm + 6 cm = 16 cm.

Obliczanie Obwodu Kwadratu

Ponieważ kwadrat ma wszystkie boki równe, obliczanie jego obwodu jest jeszcze prostsze. Jeśli długość boku kwadratu oznaczymy jako a, to wzór na obwód kwadratu wygląda następująco:

Obwód kwadratu = 4 * a

Przykład: Kwadrat ma bok długości 4 cm. Jego obwód to 4 * 4 cm = 16 cm.

Ćwiczenia praktyczne – obwód

Spróbuj teraz sam! Oblicz obwody następujących figur:

Prostokąt o długości 7 cm i szerokości 2 cm.
Kwadrat o boku 6 cm.
Prostokąt o długości 10 cm i szerokości 5 cm.

Pole Prostokąta i Kwadratu

Obliczanie Pola Prostokąta

Pole figury to miara powierzchni, którą ta figura zajmuje. Aby obliczyć pole prostokąta, musimy pomnożyć jego długość przez szerokość. Jeśli długość prostokąta oznaczymy jako a, a szerokość jako b, to wzór na pole prostokąta wygląda następująco:

Pole prostokąta = a * b

Przykład: Prostokąt ma długość 5 cm i szerokość 3 cm. Jego pole to 5 cm * 3 cm = 15 cm² (centymetrów kwadratowych).

Obliczanie Pola Kwadratu

Ponieważ kwadrat ma wszystkie boki równe, obliczanie jego pola jest jeszcze prostsze. Jeśli długość boku kwadratu oznaczymy jako a, to wzór na pole kwadratu wygląda następująco:

Pole kwadratu = a * a lub Pole kwadratu = a²

Przykład: Kwadrat ma bok długości 4 cm. Jego pole to 4 cm * 4 cm = 16 cm² (centymetrów kwadratowych).

Ćwiczenia praktyczne – pole

Teraz Twoja kolej! Oblicz pola następujących figur:

Prostokąt o długości 8 cm i szerokości 3 cm.
Kwadrat o boku 7 cm.
Prostokąt o długości 12 cm i szerokości 4 cm.

Prostokąty i Kwadraty w Życiu Codziennym

Przykłady z otoczenia

Rozejrzyj się wokół siebie! Gdzie widzisz prostokąty i kwadraty? Pomyśl o:

Książkach: Większość książek ma kształt prostokąta.
Okienach: Okna często są prostokątne lub kwadratowe.
Drzwiach: Drzwi zazwyczaj mają kształt prostokąta.
Podłogach: Płytki podłogowe często są kwadratowe lub prostokątne.
Ekranach telewizorów i monitorów komputerowych: Zazwyczaj prostokątne.

Nawet obiekty, które na pierwszy rzut oka nie wyglądają jak prostokąty lub kwadraty, mogą zawierać w sobie te figury geometryczne. Na przykład, budynki często składają się z wielu prostokątnych ścian i okien.

Praktyczne zastosowania

Znajomość właściwości prostokątów i kwadratów jest bardzo przydatna w wielu sytuacjach. Na przykład:

Planowanie ogrodu: Obliczanie pola prostokątnej grządki pomoże określić, ile roślin można na niej posadzić.
Układanie płytek: Obliczanie pola podłogi w pokoju pomoże określić, ile płytek trzeba kupić.
Budowa: Architekci i inżynierowie używają prostokątów i kwadratów do projektowania budynków i innych konstrukcji.

Matematyka otacza nas ze wszystkich stron, a zrozumienie podstawowych figur geometrycznych, takich jak prostokąty i kwadraty, jest kluczem do rozwiązywania wielu praktycznych problemów.

Rozwiązywanie Zadań Tekstowych

Często w zadaniach z matematyki spotykamy się z zadaniami tekstowymi dotyczącymi prostokątów i kwadratów. Oto kilka wskazówek, jak je rozwiązywać:

Przeczytaj uważnie treść zadania: Upewnij się, że rozumiesz, o co pytają.
Wypisz dane: Zanotuj, co już wiesz o prostokącie lub kwadracie (np. długość, szerokość, obwód, pole).
Wybierz odpowiedni wzór: Zdecyduj, czy musisz obliczyć obwód, pole, czy coś innego.
Podstaw dane do wzoru: Zastąp litery we wzorze liczbami z zadania.
Wykonaj obliczenia: Upewnij się, że robisz to dokładnie.
Zapisz odpowiedź: Nie zapomnij o jednostkach (np. cm, cm²).

Przykład zadania: Pokój ma kształt prostokąta o długości 4 metry i szerokości 3 metry. Ile metrów kwadratowych wykładziny trzeba kupić, aby wyłożyć podłogę w tym pokoju?

Rozwiązanie:

Dane: długość = 4 m, szerokość = 3 m.
Szukane: pole prostokąta.
Wzór: Pole prostokąta = a * b.
Obliczenia: Pole = 4 m * 3 m = 12 m².
Odpowiedź: Trzeba kupić 12 metrów kwadratowych wykładziny.

Podsumowanie i Następne Kroki

Gratulacje! Dotarliśmy do końca tego artykułu. Mam nadzieję, że teraz lepiej rozumiesz, czym są prostokąty i kwadraty, jak obliczać ich obwody i pola, oraz jak te figury geometryczne są obecne w naszym otoczeniu. Pamiętaj, że praktyka czyni mistrza. Im więcej będziesz rozwiązywać zadań, tym lepiej zrozumiesz te zagadnienia.

Co dalej? Spróbuj poszukać innych figur geometrycznych w swoim otoczeniu. Zastanów się, jak obliczyć ich obwody i pola. Możesz również poszukać w Internecie dodatkowych zadań i ćwiczeń. Pamiętaj, że matematyka to fascynująca przygoda, która otwiera wiele drzwi!