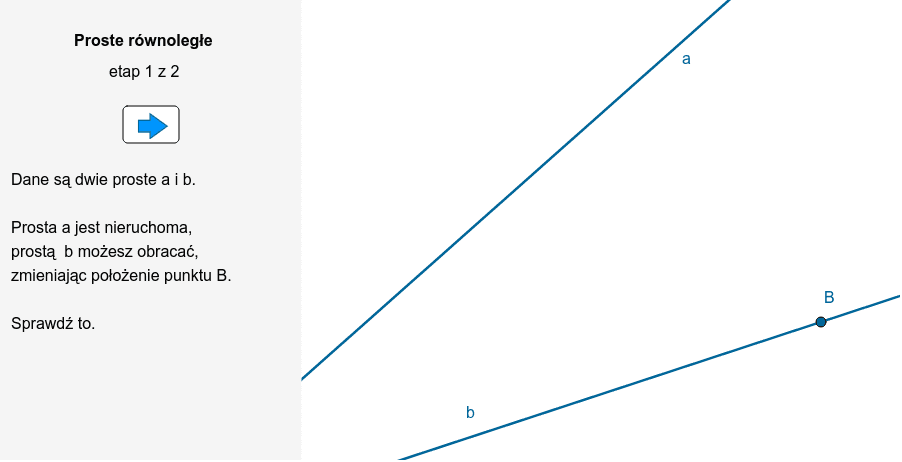Proste Prostopadłe I Proste Równoległe
Witajcie młodzi adepci geometrii! Dziś wyruszymy w fascynującą podróż po świecie linii prostych i odkryjemy dwa bardzo ważne i wszechobecne pojęcia: proste prostopadłe i proste równoległe. Przygotujcie się na wizualne eksplozje, mnóstwo przykładów z życia codziennego i obietnicę, że po tej lekcji proste już nigdy nie będą dla Was takie same!
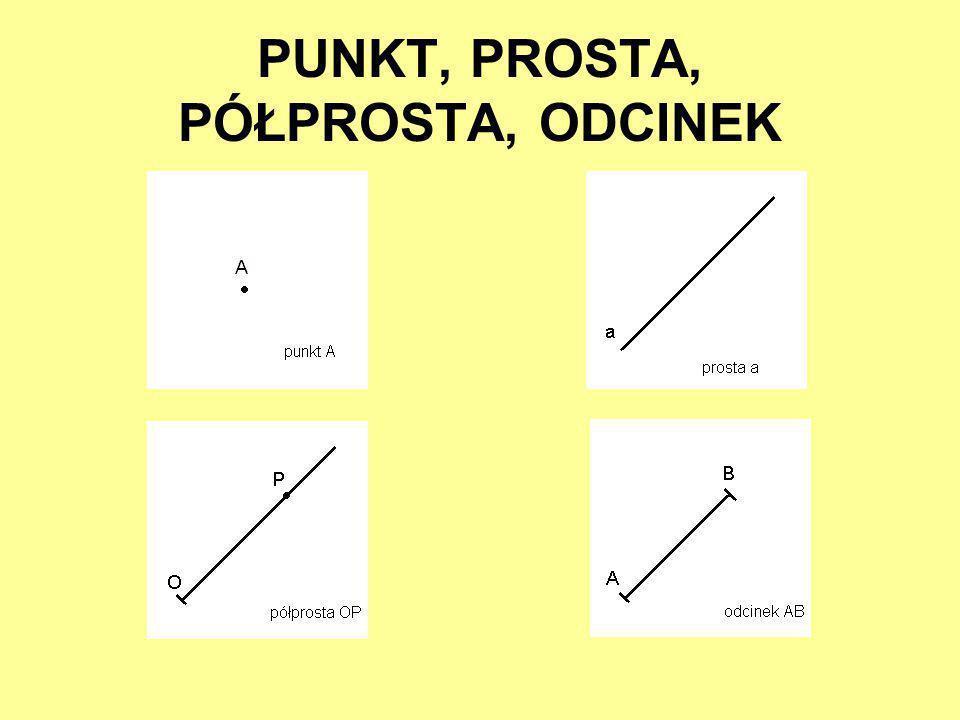
Czym w ogóle jest prosta?
Zanim przejdziemy do tych specjalnych rodzajów prostych, przypomnijmy sobie, czym właściwie jest prosta. Wyobraźcie sobie nieskończenie długą, idealnie prostą drogę, która nie ma początku ani końca. To właśnie jest prosta! Nie ma grubości, tylko długość, która ciągnie się w nieskończoność w obu kierunkach. Prostą oznaczamy zazwyczaj małą literą, np. prosta k lub l.
Proste Równoległe: Nierozłączne Przyjaciółki
Definicja i Wizualizacja
Proste równoległe to takie, które biegną obok siebie, w tej samej odległości, i nigdy, przenigdy się nie spotykają. Wyobraźcie sobie dwie tory kolejowe – bez względu na to, jak daleko pociąg pojedzie, tory zawsze będą biegły obok siebie, zachowując stałą odległość. To jest doskonały przykład prostych równoległych!
Spróbujmy jeszcze inaczej. Weźcie do ręki dwie linijki i połóżcie je na biurku tak, żeby były obok siebie, ale się nie dotykały. Upewnijcie się, że odległość między nimi jest wszędzie taka sama. Tak właśnie wyglądają proste równoległe! Możecie je przedłużać w nieskończoność, a one i tak się nie przetną.
Symbolicznie oznaczamy równoległość dwóch prostych k i l tak: k || l. To oznacza, że prosta k jest równoległa do prostej l.
Przykłady z Życia Codziennego
Proste równoległe otaczają nas wszędzie! Oto kilka przykładów:
- Tory kolejowe: Jak już wspomnieliśmy, to klasyczny przykład.
- Krawędzie zeszytu: Górna i dolna krawędź zeszytu są (zazwyczaj) równoległe, tak samo jak lewa i prawa.
- Stopnie schodów: Każdy stopień jest równoległy do następnego.
- Linie na zebry na przejściu dla pieszych: Kolejne białe pasy są ułożone równolegle.
Zauważyliście, jak ważne są proste równoległe w konstrukcjach i otoczeniu? Zapewniają porządek i stabilność.
Proste Prostopadłe: Spotkanie pod Kątem Prostym
Definicja i Wizualizacja
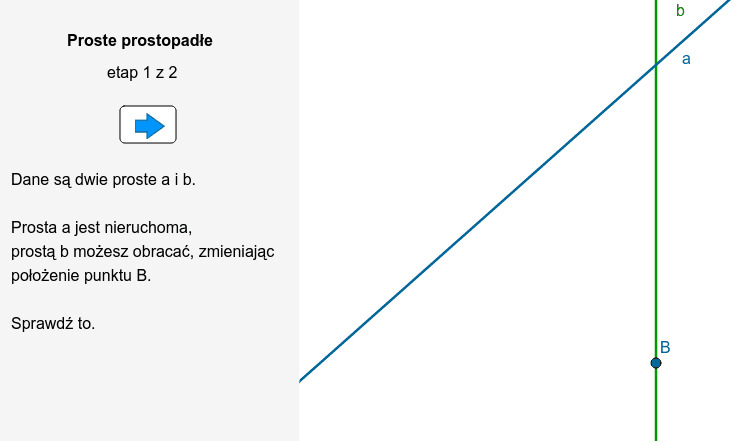
Teraz przechodzimy do prostych prostopadłych. To proste, które przecinają się pod kątem prostym, czyli pod kątem 90 stopni. Wyobraźcie sobie skrzyżowanie dwóch ulic – tam właśnie spotykają się proste prostopadłe!
Weźcie kartkę papieru i zegnijcie ją na pół. Następnie zegnijcie ją jeszcze raz na pół, tak żeby zgięte krawędzie się stykały. Powstały kąt to kąt prosty, czyli kąt między dwiema prostymi prostopadłymi.
Symbolicznie oznaczamy prostopadłość dwóch prostych k i l tak: k ⊥ l. To oznacza, że prosta k jest prostopadła do prostej l.
Przykłady z Życia Codziennego
Podobnie jak w przypadku prostych równoległych, proste prostopadłe są wszędzie wokół nas:
- Rogi pokoju: Ściany spotykają się w rogach pod kątem prostym.
- Litera "T": Pozioma kreska przecina pionową pod kątem prostym.
- Krawędzie stołu: Dwie sąsiadujące krawędzie stołu są prostopadłe.
- Krzyż: Dwie linie krzyża przecinają się pod kątem prostym.
Kąty proste są fundamentalne w architekturze i budownictwie. Zapewniają stabilność i wytrzymałość konstrukcji. Wyobraźcie sobie budynek, którego ściany nie są ustawione pod kątem prostym – bardzo szybko by się zawalił!
Kąty i Prostopadłość
Pamiętajcie, że proste prostopadłe tworzą cztery kąty proste w miejscu, gdzie się przecinają. Każdy z tych kątów ma miarę 90 stopni. To bardzo ważna informacja, która przyda się Wam w rozwiązywaniu zadań geometrycznych!
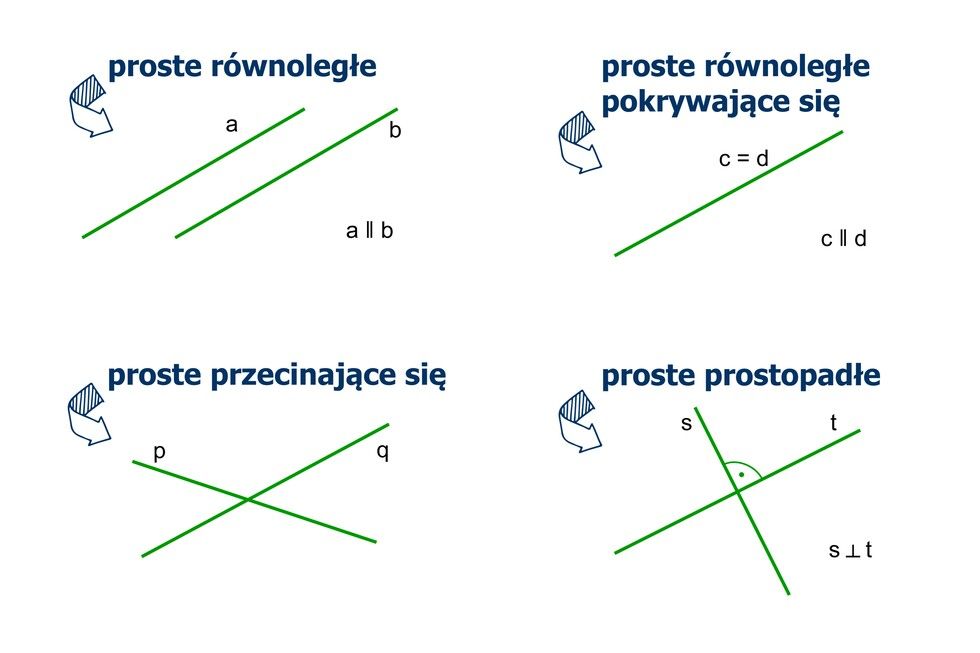
Podsumowanie: Równolegle i Prostopadle – Dwa Różne Światy
Proste równoległe biegną obok siebie i nigdy się nie spotykają, zachowując stałą odległość.
Proste prostopadłe przecinają się pod kątem prostym (90 stopni).
Zapamiętajcie te definicje i przykłady z życia codziennego. Dzięki temu łatwo będzie Wam rozpoznawać proste równoległe i prostopadłe w otaczającym świecie. Spróbujcie sami znaleźć więcej przykładów! Rozglądajcie się uważnie – geometria jest wszędzie!
Mam nadzieję, że ta lekcja rozjaśniła Wam różnice między prostymi równoległymi i prostopadłymi. Teraz z pewnością poradzicie sobie z zadaniami i będziecie mogli z dumą powiedzieć: "Rozumiem proste!"

.jpg)