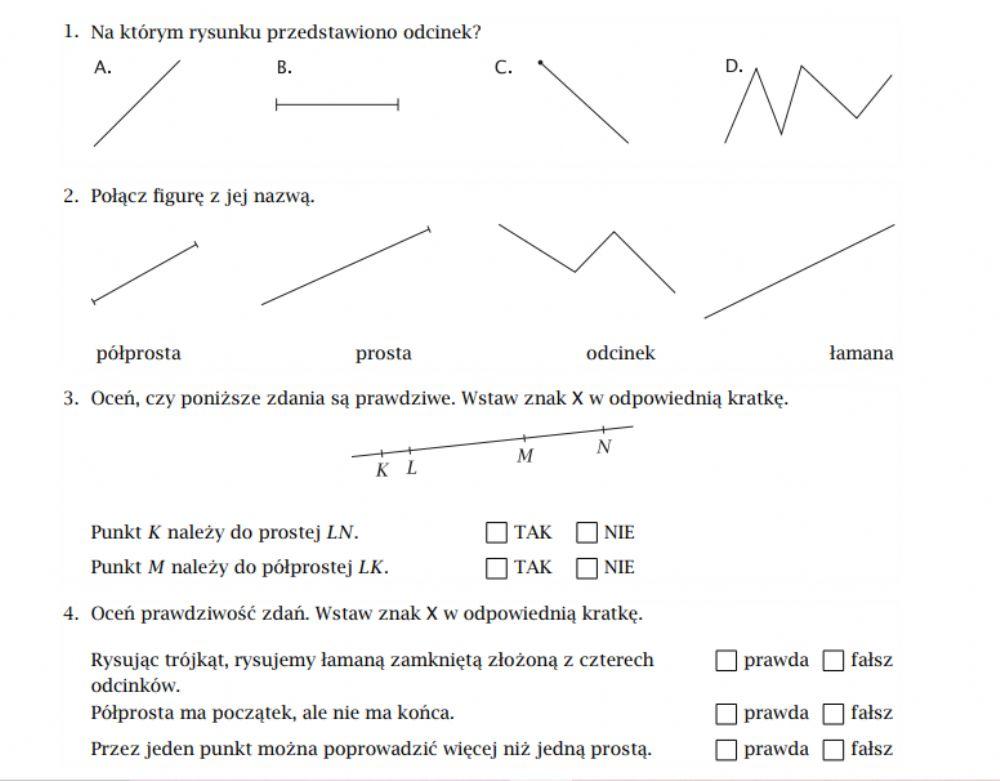
Prosta Półprosta Odcinek Sprawdzian Kl 4 Wsip

Czy pamiętasz, jak w czwartej klasie podstawówki geometria wydawała się czymś tajemniczym i skomplikowanym? Linie proste, półproste, odcinki… Sprawdzian z tego materiału potrafił przyprawić o ból głowy! Wiele dzieci (i rodziców!) miało trudności z rozróżnieniem tych pojęć. Postaramy się to dzisiaj rozwiać i pomóc lepiej zrozumieć te podstawy geometrii.

Linia prosta, półprosta i odcinek - czym się różnią?

Zacznijmy od podstaw. Geometria, choć na początku wydaje się trudna, opiera się na prostych zasadach. Wyjaśnimy to krok po kroku, unikając skomplikowanego języka.

Linia prosta

Wyobraź sobie linię, która biegnie w nieskończoność w obie strony. Nie ma początku ani końca. Możemy ją przedłużać w nieskończoność. To właśnie jest linia prosta. Oznacza się ją najczęściej małymi literami alfabetu, np. "k" lub "l". Na rysunkach symbolizujemy ją strzałkami na obu końcach, aby pokazać, że ciągnie się bez końca.

Linia prosta jest fundamentalnym pojęciem w geometrii. Wiele innych figur geometrycznych (kąty, trójkąty, etc.) jest zbudowanych z odcinków prostych lub ich fragmentów. Zrozumienie, że linia prosta nie ma końca, jest kluczowe do dalszej nauki.

Półprosta

Półprosta to jakby "połowa" prostej. Ma początek (punkt, z którego się zaczyna), ale nie ma końca w drugim kierunku. Wyobraź sobie promień światła wychodzący ze słońca. To idealny przykład półprostej. Oznaczamy ją dwoma punktami: punktem początkowym i dowolnym innym punktem leżącym na tej półprostej. Zapisujemy to np. jako AB, gdzie A jest punktem początkowym, a B jest dowolnym innym punktem na półprostej. Strzałka nad zapisem AB (w kierunku punktu B) symbolizuje, że półprosta rozciąga się w nieskończoność w kierunku B.

Ważne! Kolejność punktów w oznaczeniu półprostej jest istotna! AB to nie to samo, co BA. AB zaczyna się w punkcie A i biegnie w kierunku B, natomiast BA zaczynałaby się w punkcie B i biegła w kierunku A.

Odcinek

Odcinek to fragment prostej, który ma początek i koniec. Możemy go zmierzyć. Na przykład, bok kwadratu jest odcinkiem. Oznaczamy go dwoma punktami - punktem początkowym i końcowym. Zapisujemy to np. jako CD (lub DC – w przypadku odcinka kolejność punktów nie ma znaczenia). Nad zapisem CD nie rysujemy strzałki, ponieważ odcinek jest skończony i nie biegnie w nieskończoność.

Pomyśl o krawędzi stołu, drodze między dwoma miastami na mapie, czy ołówku. Wszystkie te rzeczy mają początek i koniec, więc są doskonałymi przykładami odcinków.

Przygotowanie do sprawdzianu z geometrii - praktyczne wskazówki

Jak więc przygotować dziecko do sprawdzianu z geometrii w czwartej klasie? Oto kilka praktycznych wskazówek:

Zrozumienie, a nie tylko zapamiętywanie. Ważne jest, aby dziecko rozumiało, dlaczego linia prosta jest nieskończona, a odcinek ma początek i koniec. Używaj przykładów z życia codziennego, aby zobrazować te pojęcia.
Rysowanie i wizualizacja. Zachęć dziecko do rysowania linii prostych, półprostych i odcinków. Rysowanie pomaga utrwalić wiedzę.
Ćwiczenia praktyczne. Rozwiązywanie zadań jest kluczowe. Im więcej zadań dziecko rozwiąże, tym lepiej zrozumie materiał. Warto poszukać dodatkowych ćwiczeń w internecie lub w podręcznikach.
Przykładowe zadania. Poproś dziecko, aby wskazało linie proste, półproste i odcinki w otoczeniu. Może to być na rysunku, w pokoju lub na spacerze.
Gry edukacyjne. Istnieją gry edukacyjne, które w zabawny sposób pomagają utrwalić wiedzę z geometrii.
Powtórka materiału. Regularnie powtarzaj materiał z dzieckiem. Nawet krótkie sesje powtórkowe pomogą utrwalić wiedzę.

Przykładowe zadania na sprawdzianie

Jakie zadania mogą pojawić się na sprawdzianie?

Rozpoznawanie i nazywanie linii prostych, półprostych i odcinków na rysunkach.
Rysowanie linii prostych, półprostych i odcinków zgodnie z podanymi warunkami.
Porównywanie długości odcinków.
Zadania tekstowe związane z liniami prostymi, półprostymi i odcinkami. Na przykład: "Narysuj odcinek AB o długości 5 cm."

Pamiętaj, że kluczem do sukcesu jest cierpliwość i pozytywne nastawienie. Ucz się razem z dzieckiem i spraw, aby nauka geometrii była zabawą, a nie przykrym obowiązkiem!

Zatem, drogi rodzicu (lub uczniu!), uzbrojony w tę wiedzę, możesz śmiało przystąpić do nauki geometrii. Pamiętaj, że praktyka czyni mistrza! Powodzenia na sprawdzianie!