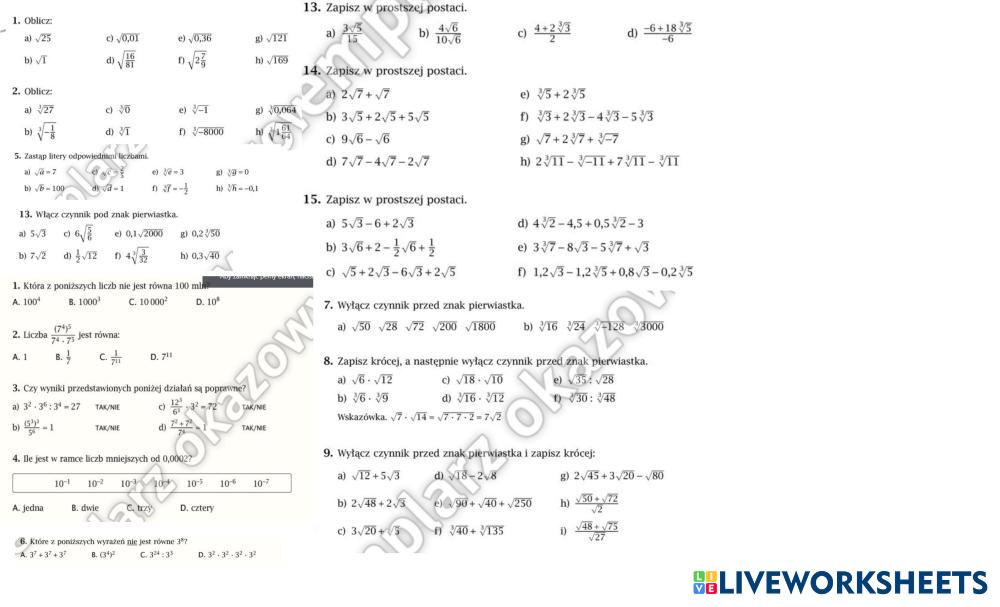
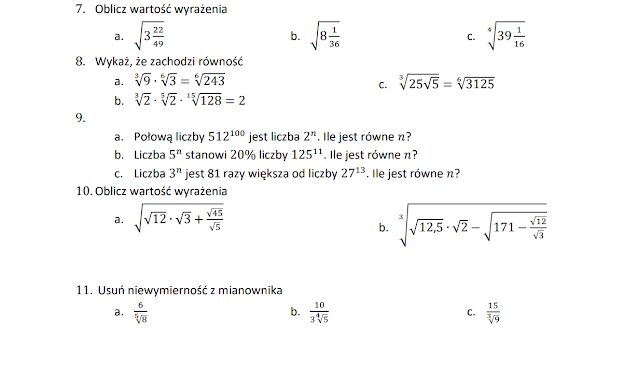Potęgi I Pierwiastki Klasa 7

Wyobraź sobie, że próbujesz obliczyć pole kwadratu, znając tylko długość jego boku. Albo, że chcesz sprawiedliwie podzielić skarb pomiędzy przyjaciół, gdzie liczba skrzyń skrywa się pod pierwiastkiem. Brzmi znajomo? Jeśli jesteś uczniem klasy 7, to na pewno spotkałeś się już z potęgami i pierwiastkami! Ten artykuł jest właśnie dla Ciebie – pomoże Ci zrozumieć, jak działają te zagadnienia matematyczne i pokaże, że wcale nie są takie straszne, jak się wydają.

Czym są potęgi?

Potęgowanie to skrócony zapis mnożenia tej samej liczby przez samą siebie. Pomyśl o tym jak o sposobie na szybkie liczenie, gdy masz wiele identycznych czynników.

Ogólny wzór wygląda następująco: aⁿ = a * a * a * ... * a (n razy)

Gdzie:

• a to podstawa potęgi – liczba, którą mnożymy.
• n to wykładnik potęgi – liczba, która mówi nam, ile razy mnożymy podstawę przez samą siebie.

Przykłady:

• 2³ = 2 * 2 * 2 = 8 (2 do potęgi 3 równa się 8)
• 5² = 5 * 5 = 25 (5 do potęgi 2 równa się 25)
• 10⁴ = 10 * 10 * 10 * 10 = 10000 (10 do potęgi 4 równa się 10000)

Zauważ, że podnosząc liczbę do potęgi, nie mnożymy jej przez wykładnik! Często popełniany błąd to mylenie 2³ z 2 * 3. Pamiętaj: potęgowanie to powtarzane mnożenie tej samej liczby!

Specjalne przypadki potęg

Istnieją pewne szczególne sytuacje, o których warto pamiętać:

• Dowolna liczba podniesiona do potęgi 1 równa się samej sobie: a¹ = a (np. 7¹ = 7)
• Dowolna liczba (oprócz 0) podniesiona do potęgi 0 równa się 1: a⁰ = 1 (np. 15⁰ = 1, ale 0⁰ jest nieokreślone)
• 1 podniesiona do dowolnej potęgi równa się 1: 1ⁿ = 1 (np. 1¹⁰⁰ = 1)
• 0 podniesiona do dowolnej potęgi różnej od 0 równa się 0: 0ⁿ = 0 (np. 0⁵ = 0)

Prawa działań na potęgach

Znamy już definicję potęg, teraz czas na poznanie praw działań na potęgach. Ułatwią nam one upraszczanie wyrażeń i rozwiązywanie zadań.

• Mnożenie potęg o tych samych podstawach: a^m * aⁿ = a^m+n (np. 2³ * 2² = 2³⁺² = 2⁵ = 32) Wyobraź sobie, że masz 3 dwójki pomnożone przez siebie, a potem jeszcze 2. Razem masz ich 5!
• Dzielenie potęg o tych samych podstawach: a^m / aⁿ = a^m-n (np. 5⁷ / 5³ = 5^7-3 = 5⁴ = 625) Dzielenie potęg to tak jakbyśmy "odcinali" pewną liczbę czynników.
• Potęgowanie potęgi: (a^m)ⁿ = a^m*n (np. (3²)³ = 3^2*3 = 3⁶ = 729) To tak jakbyśmy mieli kilka grup potęg.
• Potęgowanie iloczynu: (a * b)ⁿ = aⁿ * bⁿ (np. (2 * 3)² = 2² * 3² = 4 * 9 = 36) Możemy rozdzielić potęgę na każdy czynnik.
• Potęgowanie ilorazu: (a / b)ⁿ = aⁿ / bⁿ (np. (6 / 2)³ = 6³ / 2³ = 216 / 8 = 27) Podobnie jak z iloczynem, potęgę możemy rozdzielić.

Pamiętaj, aby stosować te prawa tylko wtedy, gdy podstawy potęg są takie same (przy mnożeniu i dzieleniu) lub gdy masz do czynienia z iloczynem lub ilorazem w nawiasie.

Czym są pierwiastki?

Pierwiastkowanie to działanie odwrotne do potęgowania. Szukamy liczby, która podniesiona do danej potęgi da nam zadaną liczbę.

Ogólny zapis pierwiastka wygląda tak: ⁿ√a = b

Gdzie:

• n to stopień pierwiastka – mówi nam, do jakiej potęgi musimy podnieść wynik, aby otrzymać liczbę pod pierwiastkiem. Jeśli n = 2, mówimy o pierwiastku kwadratowym i zazwyczaj nie piszemy 2 (√a).
• a to liczba podpierwiastkowa – liczba, z której wyciągamy pierwiastek.
• b to wynik pierwiastkowania – liczba, która podniesiona do potęgi n daje a.

Przykłady:

• √25 = 5 (pierwiastek kwadratowy z 25 równa się 5, ponieważ 5² = 25)
• ³√8 = 2 (pierwiastek trzeciego stopnia z 8 równa się 2, ponieważ 2³ = 8)
• ⁴√16 = 2 (pierwiastek czwartego stopnia z 16 równa się 2, ponieważ 2⁴ = 16)

Pierwiastek kwadratowy jest najczęściej spotykanym pierwiastkiem. Zastanów się, jaka liczba pomnożona przez samą siebie da nam liczbę pod pierwiastkiem. To właśnie jest wynik pierwiastkowania.

Pierwiastki z liczb ujemnych

W klasie 7 zazwyczaj zajmujemy się pierwiastkami z liczb nieujemnych (zero i liczby dodatnie). Pierwiastki o parzystym stopniu (np. pierwiastek kwadratowy, pierwiastek czwartego stopnia) z liczb ujemnych nie istnieją w zbiorze liczb rzeczywistych. Dlaczego? Bo żadna liczba podniesiona do parzystej potęgi nie da nam wyniku ujemnego.

Natomiast pierwiastki o nieparzystym stopniu z liczb ujemnych istnieją! Np. ³√-8 = -2, bo (-2)³ = -8.

Działania na pierwiastkach

Podobnie jak z potęgami, również z pierwiastkami możemy wykonywać pewne działania, pamiętając o kilku zasadach.

• Pierwiastek z iloczynu: ⁿ√(a * b) = ⁿ√a * ⁿ√b (np. √ (4 * 9) = √4 * √9 = 2 * 3 = 6) Możemy rozdzielić pierwiastek na każdy czynnik, pod warunkiem, że mają ten sam stopień.
• Pierwiastek z ilorazu: ⁿ√(a / b) = ⁿ√a / ⁿ√b (np. √(100 / 4) = √100 / √4 = 10 / 2 = 5) Podobnie jak z iloczynem, możemy rozdzielić pierwiastek, jeśli mają ten sam stopień.

Uwaga! ⁿ√(a + b) ≠ ⁿ√a + ⁿ√b oraz ⁿ√(a - b) ≠ ⁿ√a - ⁿ√b. Nie możemy rozdzielać pierwiastków dla sum i różnic!

Potęgi i pierwiastki w praktyce

Potęgi i pierwiastki nie są tylko abstrakcyjnymi pojęciami matematycznymi. Używamy ich na co dzień, często nawet o tym nie wiedząc!

• Obliczanie pól i objętości: Jak już wspomnieliśmy na początku, pole kwadratu to a², a objętość sześcianu to a³. Potęgi są niezbędne do obliczania tych wielkości.
• Skala na mapach: Skala mapy często jest podawana w postaci potęgi liczby 10 (np. 1:100000).
• Informatyka: Potęgi dwójki są podstawą systemu binarnego, na którym opiera się działanie komputerów. Pojemność dysków i pamięci wyrażana jest w bajtach, kilobajtach, megabajtach, gigabajtach, itd. (1 KB = 2¹⁰ B, 1 MB = 2²⁰ B, itd.).
• Nauki przyrodnicze: Wzory opisujące zjawiska fizyczne i chemiczne często zawierają potęgi i pierwiastki.
• Finanse: Obliczanie odsetek składanych wymaga użycia potęg.

Zrozumienie potęg i pierwiastków otwiera drzwi do wielu dziedzin nauki i techniki. To fundament, na którym buduje się bardziej zaawansowaną wiedzę matematyczną.

Jak skutecznie uczyć się potęg i pierwiastków?

Oto kilka wskazówek, które pomogą Ci opanować potęgi i pierwiastki:

• Zacznij od podstaw: Upewnij się, że rozumiesz definicje potęgi, wykładnika, podstawy, pierwiastka, stopnia pierwiastka i liczby podpierwiastkowej.
• Ćwicz, ćwicz i jeszcze raz ćwicz: Rozwiązuj jak najwięcej zadań. Im więcej ćwiczysz, tym lepiej utrwalisz wiedzę i zdobędziesz wprawę.
• Korzystaj z zasobów online: W internecie znajdziesz wiele darmowych materiałów edukacyjnych, interaktywnych ćwiczeń i filmów instruktażowych.
• Nie bój się pytać: Jeśli masz jakieś wątpliwości, nie wstydź się zapytać nauczyciela, rodzica lub kolegę.
• Stosuj potęgi i pierwiastki w praktyce: Spróbuj znaleźć przykłady zastosowania potęg i pierwiastków w życiu codziennym. To pomoże Ci lepiej zrozumieć, jak działają i dlaczego są tak ważne.
• Ucz się w grupie: Uczenie się z kolegami może być bardziej efektywne i przyjemne. Możecie sobie wzajemnie pomagać, wyjaśniać trudne zagadnienia i rozwiązywać zadania.

Pamiętaj, że nauka matematyki wymaga czasu i wysiłku. Nie zrażaj się, jeśli na początku coś Ci nie wychodzi. Bądź cierpliwy, systematyczny i wytrwały, a na pewno osiągniesz sukces!

Podsumowanie

Potęgi i pierwiastki to fundamentalne zagadnienia matematyczne, które mają szerokie zastosowanie w życiu codziennym i w wielu dziedzinach nauki. Zrozumienie ich działania i praw pozwala na sprawne rozwiązywanie problemów i otwiera drzwi do dalszej edukacji matematycznej i technicznej.

Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć potęgi i pierwiastki. Pamiętaj, ćwiczenie czyni mistrza! Im więcej zadań rozwiążesz, tym pewniej będziesz się czuł w tym temacie. Powodzenia w dalszej nauce!