Postać Ogólna Kanoniczna I Iloczynowa Funkcji Kwadratowej

Funkcja kwadratowa to jeden z fundamentów matematyki szkolnej, pojawiająca się na wielu poziomach edukacji. Jej zrozumienie jest kluczowe do opanowania bardziej zaawansowanych zagadnień. Funkcję kwadratową możemy zapisać na trzy różne sposoby: postać ogólną, kanoniczną i iloczynową. Każda z tych postaci ujawnia inne własności funkcji i jest przydatna w różnych sytuacjach. Przejdźmy zatem do szczegółowego omówienia każdej z nich.

Postać ogólna funkcji kwadratowej prezentuje się następująco:

f(x) = ax² + bx + c,

gdzie a, b i c to współczynniki liczbowe, a ≠ 0. Współczynnik 'a' decyduje o kierunku ramion paraboli: jeśli a > 0, ramiona skierowane są do góry, a jeśli a < 0, ramiona skierowane są do dołu. Współczynnik 'c' określa punkt przecięcia paraboli z osią OY. Jest to wartość funkcji dla x = 0, czyli f(0) = c. Współczynnik 'b' wpływa na położenie wierzchołka paraboli, ale jego wpływ nie jest tak bezpośredni jak w przypadku 'a' i 'c'.

Analizując postać ogólną, możemy wyznaczyć wiele istotnych informacji o funkcji. Przede wszystkim, możemy obliczyć wyróżnik kwadratowy, oznaczany grecką literą Δ (delta):

Δ = b² - 4ac.

Wartość wyróżnika informuje nas o liczbie miejsc zerowych funkcji kwadratowej. Jeśli Δ > 0, funkcja ma dwa różne miejsca zerowe. Jeśli Δ = 0, funkcja ma jedno miejsce zerowe (wierzchołek paraboli leży na osi OX). Jeśli Δ < 0, funkcja nie ma miejsc zerowych (parabola nie przecina osi OX).

Miejsca zerowe funkcji kwadratowej, oznaczane jako x₁ i x₂, możemy obliczyć ze wzorów:

x₁ = (-b - √Δ) / 2a x₂ = (-b + √Δ) / 2a

W przypadku, gdy Δ = 0, oba wzory sprowadzają się do jednego:

x = -b / 2a

który to wzór daje nam współrzędną x wierzchołka paraboli.

Znając postać ogólną funkcji, możemy również obliczyć współrzędne wierzchołka paraboli W = (p, q). Współrzędną x wierzchołka (p) obliczamy ze wzoru:

p = -b / 2a

a współrzędną y wierzchołka (q) możemy obliczyć na dwa sposoby:

q = f(p) = ap² + bp + c lub q = -Δ / 4a

Wykorzystanie postaci ogólnej pozwala nam na szkicowanie wykresu funkcji kwadratowej. Znając kierunek ramion (znak 'a'), punkt przecięcia z osią OY (wartość 'c'), liczbę i położenie miejsc zerowych (na podstawie Δ i wzorów na x₁ i x₂) oraz współrzędne wierzchołka (p i q), możemy z dużą dokładnością narysować parabolę.

Postać kanoniczna funkcji kwadratowej

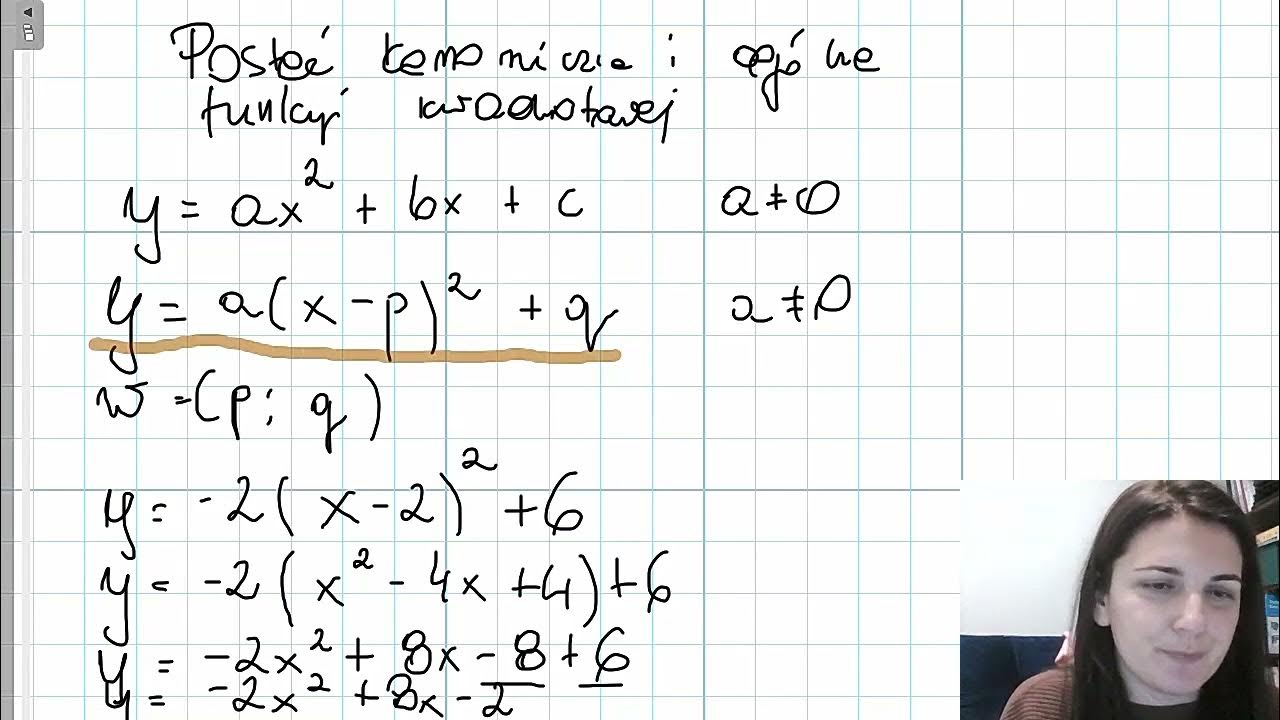
Postać kanoniczna funkcji kwadratowej wygląda następująco:

f(x) = a(x - p)² + q,

gdzie 'a' jest tym samym współczynnikiem co w postaci ogólnej, a (p, q) to współrzędne wierzchołka paraboli.

Postać kanoniczna jest niezwykle przydatna, ponieważ bezpośrednio ujawnia współrzędne wierzchołka paraboli. Widzimy od razu, gdzie znajduje się wierzchołek, co ułatwia szkicowanie wykresu funkcji. Dodatkowo, na podstawie 'a' i 'q' możemy określić zbiór wartości funkcji. Jeśli a > 0, to zbiór wartości to <q, ∞), a jeśli a < 0, to zbiór wartości to (-∞, q>.

Przejście z postaci ogólnej do kanonicznej wymaga pewnych przekształceń algebraicznych. Możemy to zrobić, wykorzystując wzory na współrzędne wierzchołka:

p = -b / 2a q = -Δ / 4a

Następnie, wstawiamy wartości 'a', 'p' i 'q' do postaci kanonicznej. Innym sposobem jest tzw. dopełnianie do pełnego kwadratu. Polega ono na przekształceniu wyrażenia ax² + bx + c do postaci a(x - p)² + q. Dla przykładu, rozważmy funkcję f(x) = x² + 4x + 3. Chcemy doprowadzić ją do postaci (x - p)² + q.

Zauważmy, że (x + 2)² = x² + 4x + 4. Zatem możemy zapisać:

x² + 4x + 3 = (x² + 4x + 4) - 4 + 3 = (x + 2)² - 1.

W tym przypadku, p = -2, q = -1, a więc wierzchołek paraboli znajduje się w punkcie W = (-2, -1).

Przejście z postaci kanonicznej do ogólnej jest prostsze. Wystarczy rozwinąć kwadrat i uporządkować wyrazy:

f(x) = a(x - p)² + q = a(x² - 2px + p²) + q = ax² - 2apx + ap² + q.

Zatem, b = -2ap, a c = ap² + q.

Postać iloczynowa funkcji kwadratowej

Postać iloczynowa funkcji kwadratowej istnieje tylko wtedy, gdy funkcja ma miejsca zerowe, czyli gdy Δ ≥ 0. Prezentuje się ona następująco:

f(x) = a(x - x₁)(x - x₂),

gdzie 'a' jest tym samym współczynnikiem co w postaci ogólnej i kanonicznej, a x₁ i x₂ to miejsca zerowe funkcji.

Postać iloczynowa jest niezwykle użyteczna, gdy chcemy szybko odczytać miejsca zerowe funkcji. Widzimy je bezpośrednio z zapisu. Jeśli x₁ i x₂ są różne, to funkcja ma dwa różne miejsca zerowe. Jeśli x₁ = x₂, to funkcja ma jedno miejsce zerowe (wierzchołek paraboli leży na osi OX).

Przejście z postaci ogólnej do iloczynowej wymaga obliczenia miejsc zerowych, co wiąże się z obliczeniem wyróżnika Δ i zastosowaniem odpowiednich wzorów. Następnie, wstawiamy wartości 'a', x₁ i x₂ do postaci iloczynowej.

Przejście z postaci iloczynowej do ogólnej również polega na rozwijaniu i uporządkowaniu wyrażeń:

f(x) = a(x - x₁)(x - x₂) = a(x² - x₂x - x₁x + x₁x₂) = a(x² - (x₁ + x₂)x + x₁x₂) = ax² - a(x₁ + x₂)x + ax₁x₂.

Zatem, b = -a(x₁ + x₂), a c = ax₁x₂.

Analizując postać iloczynową, możemy zauważyć pewne zależności między współczynnikami funkcji a miejscami zerowymi. Suma miejsc zerowych wynosi:

x₁ + x₂ = -b / a

a iloczyn miejsc zerowych wynosi:

x₁ * x₂ = c / a

Te zależności są znane jako wzory Viète'a.

Podsumowując, każda z postaci funkcji kwadratowej ma swoje zalety i wady. Postać ogólna pozwala na obliczenie wyróżnika i miejsc zerowych. Postać kanoniczna ujawnia współrzędne wierzchołka. Postać iloczynowa ujawnia miejsca zerowe (o ile istnieją). Zrozumienie tych trzech postaci i umiejętność przechodzenia między nimi jest kluczowe do rozwiązywania problemów związanych z funkcją kwadratową. W zależności od zadania, jedna postać może być bardziej użyteczna niż inna. Umiejętność rozpoznawania, która postać będzie najbardziej odpowiednia, jest cechą biegłego matematyka.