Porównywanie Ułamków O Różnych Licznikach I Mianownikach

Porównywanie ułamków o różnych licznikach i mianownikach może początkowo wydawać się wyzwaniem, ale z odpowiednim podejściem staje się całkiem proste. Pokażę kilka strategii, które pomogą Ci w tym procesie.

Najprostszym sposobem na porównanie ułamków jest sprowadzenie ich do wspólnego mianownika. Weźmy na przykład ułamki 2/3 i 3/4. Znajdujemy najmniejszą wspólną wielokrotność (NWW) mianowników, czyli 3 i 4. NWW(3,4) to 12.

Następnie każdy ułamek rozszerzamy tak, aby miał mianownik równy 12. Ułamek 2/3 mnożymy przez 4/4 (co jest równe 1) co daje nam (24)/(34) = 8/12. Ułamek 3/4 mnożymy przez 3/3, co daje nam (33)/(43) = 9/12.

Teraz porównujemy ułamki 8/12 i 9/12. Ponieważ mają ten sam mianownik, możemy porównać liczniki. 8 jest mniejsze od 9, więc 8/12 < 9/12. Zatem 2/3 < 3/4.

Inna metoda polega na sprowadzeniu ułamków do wspólnego licznika. Rozważmy ułamki 5/7 i 5/8. Mamy już wspólny licznik, czyli 5. Teraz skupiamy się na mianownikach. Im większy mianownik, tym mniejsza wartość ułamka, jeśli liczniki są takie same. Ponieważ 7 < 8, to 5/7 > 5/8.

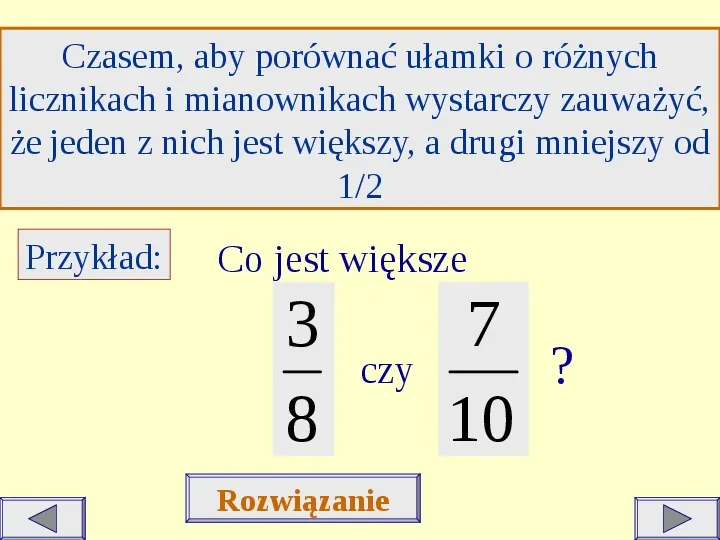
Można też skorzystać z metody porównywania do 1/2. Weźmy ułamki 3/7 i 4/6. Zastanówmy się, czy każdy z nich jest większy, mniejszy, czy równy 1/2.

Ułamek 3/7 jest mniejszy od 1/2, ponieważ 3 jest mniejsze niż połowa z 7 (3.5). Ułamek 4/6 jest większy od 1/2, ponieważ 4 jest większe niż połowa z 6 (3). Zatem, skoro 3/7 < 1/2 i 4/6 > 1/2, to 3/7 < 4/6.

Można też spróbować przekształcić ułamki na postać dziesiętną. Weźmy ułamki 1/3 i 2/5. Ułamek 1/3 to około 0.333, a ułamek 2/5 to 0.4. Porównując 0.333 i 0.4, widać, że 0.333 < 0.4, więc 1/3 < 2/5.

Czasami można po prostu oszacować wartości ułamków i na tej podstawie je porównać. Rozważmy ułamki 7/15 i 11/20. 7/15 jest nieco mniejsze od 1/2 (ponieważ połowa z 15 to 7.5). 11/20 jest nieco większe od 1/2 (ponieważ połowa z 20 to 10). Zatem 7/15 < 11/20.

Spróbujmy teraz trudniejszego przykładu: 9/16 i 12/21. Sprowadzimy je do wspólnego mianownika. NWW(16, 21) to 336. Rozszerzamy ułamki: 9/16 mnożymy przez 21/21, co daje 189/336. 12/21 mnożymy przez 16/16, co daje 192/336. Ponieważ 189 < 192, to 189/336 < 192/336, czyli 9/16 < 12/21.

Innym przykładem jest porównanie 4/9 i 7/15. NWW(9,15) = 45. 4/9 mnożymy przez 5/5, co daje 20/45. 7/15 mnożymy przez 3/3, co daje 21/45. Zatem 20/45 < 21/45, czyli 4/9 < 7/15.

A co z ułamkami 13/25 i 17/30? NWW(25,30) = 150. 13/25 mnożymy przez 6/6, co daje 78/150. 17/30 mnożymy przez 5/5, co daje 85/150. Zatem 78/150 < 85/150, czyli 13/25 < 17/30.

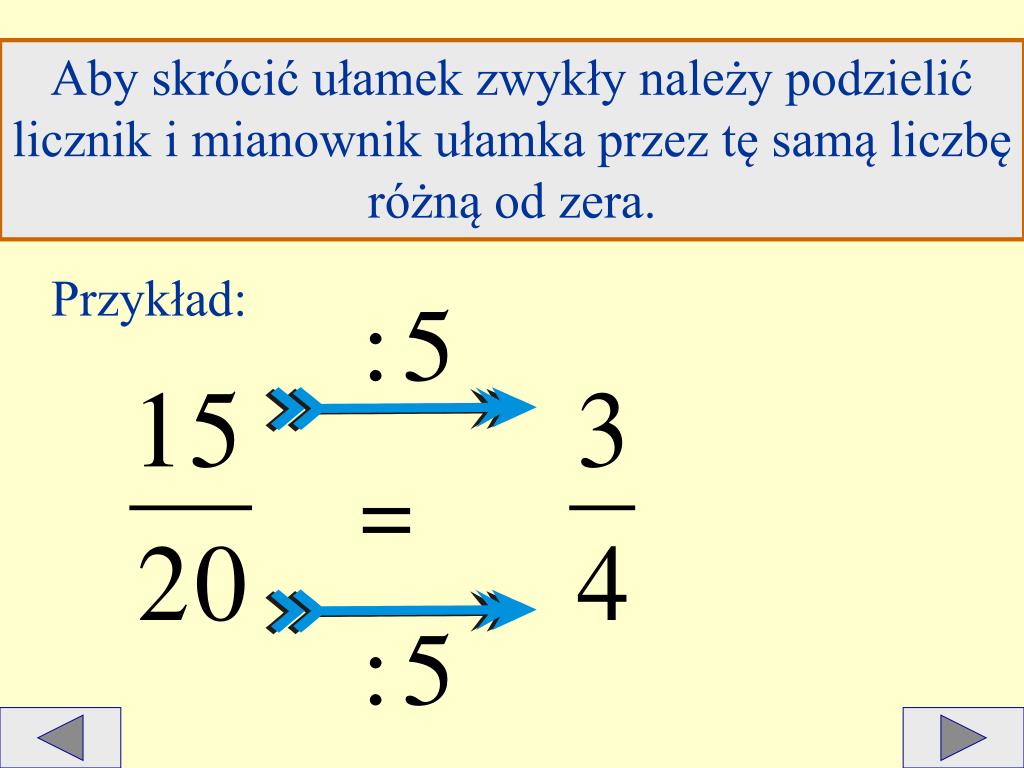
Kiedy mamy do czynienia z większymi liczbami, warto poszukać możliwości uproszczenia ułamków przed porównaniem. Na przykład, jeśli mamy ułamki 24/36 i 18/24, możemy uprościć 24/36 dzieląc licznik i mianownik przez 12, co daje 2/3. Ułamek 18/24 upraszczamy dzieląc licznik i mianownik przez 6, co daje 3/4. Teraz porównujemy 2/3 i 3/4, co już wiemy, że 2/3 < 3/4.

Jeszcze jeden przykład: 35/49 i 45/63. 35/49 upraszczamy dzieląc przez 7, otrzymując 5/7. 45/63 upraszczamy dzieląc przez 9, otrzymując 5/7. Zatem 35/49 = 45/63.

Ułamki a Procenty

Ciekawą techniką jest przekształcanie ułamków na procenty. Wiemy, że 1/4 to 25%, 1/2 to 50%, a 3/4 to 75%. Spróbujmy porównać ułamki 7/10 i 6/8. 7/10 to 70%. Ułamek 6/8 możemy uprościć do 3/4, co daje 75%. Zatem 7/10 < 6/8.

A co z 11/20 i 13/25? 11/20 mnożymy przez 5/5, otrzymując 55/100, czyli 55%. 13/25 mnożymy przez 4/4, otrzymując 52/100, czyli 52%. Zatem 11/20 > 13/25.

Inne Strategie Porównywania

Można również użyć metody "mnożenia na krzyż". Dla ułamków a/b i c/d, mnożymy a przez d i b przez c. Jeśli ad > bc, to a/b > c/d. Jeśli ad < bc, to a/b < c/d. Jeśli ad = bc, to a/b = c/d.

Weźmy ułamki 3/5 i 2/7. Mnożymy 3 * 7 = 21 i 5 * 2 = 10. Ponieważ 21 > 10, to 3/5 > 2/7.

Sprawdźmy jeszcze raz: 4/9 i 5/11. 4 * 11 = 44, a 9 * 5 = 45. Ponieważ 44 < 45, to 4/9 < 5/11.

Kolejny przykład: 7/12 i 9/16. 7 * 16 = 112, a 12 * 9 = 108. Ponieważ 112 > 108, to 7/12 > 9/16.

Podsumowując, porównywanie ułamków o różnych licznikach i mianownikach wymaga zastosowania jednej z kilku strategii. Możemy sprowadzić ułamki do wspólnego mianownika, wspólnego licznika, porównywać je do 1/2, przekształcać na postać dziesiętną lub procentową, stosować metodę mnożenia na krzyż, a czasem po prostu oszacować ich wartości. Wybór strategii zależy od konkretnych ułamków, z którymi mamy do czynienia. Im więcej ćwiczysz, tym łatwiej będzie Ci wybrać najskuteczniejszą metodę. Pamiętaj o upraszczaniu ułamków, gdy to tylko możliwe, aby ułatwić obliczenia.