Ponizej Narysowano Ostroslupy Prawidlowe Czworokatne Oblicz Dlugosci

Dobrze, przygotujmy się do wyjaśnienia, jak obliczyć długości w ostrosłupach prawidłowych czworokątnych. Poniżej znajdziecie szczegółowe omówienie różnych przypadków i wzorów, które pomogą wam rozwiązać zadania.

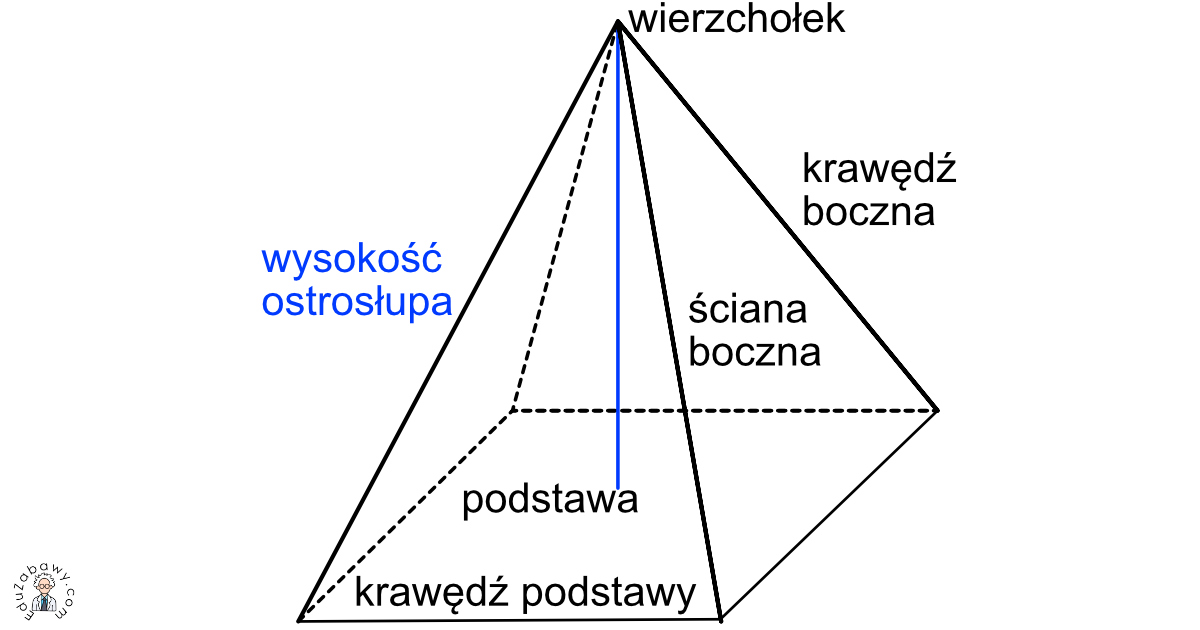
W ostrosłupie prawidłowym czworokątnym mamy do czynienia z podstawą w kształcie kwadratu i ścianami bocznymi, które są trójkątami równoramiennymi. Kluczowe elementy, które musimy rozważyć przy obliczeniach to:

a – długość krawędzi podstawy (kwadratu)
h – wysokość ostrosłupa (od wierzchołka do środka podstawy)
H – wysokość ściany bocznej (od wierzchołka ściany bocznej do środka krawędzi podstawy)
b – długość krawędzi bocznej (od wierzchołka ostrosłupa do wierzchołka kwadratu w podstawie)
d – długość przekątnej podstawy (kwadratu)

Podstawowe zależności:

Przekątna kwadratu (d): d = a√2
Związek między wysokością ostrosłupa (h), połową przekątnej podstawy (d/2) i krawędzią boczną (b): b² = h² + (d/2)² czyli b² = h² + (a√2 / 2)² więc b² = h² + (a²/2)
Związek między wysokością ostrosłupa (h), połową krawędzi podstawy (a/2) i wysokością ściany bocznej (H): H² = h² + (a/2)²
Związek między krawędzią boczną (b), połową krawędzi podstawy (a/2) i wysokością ściany bocznej (H): b² = H² + (a/2)²

Przykłady obliczeń:

Załóżmy, że mamy ostrosłup prawidłowy czworokątny, w którym znamy długość krawędzi podstawy (a) i wysokość ostrosłupa (h). Chcemy obliczyć długość krawędzi bocznej (b) i wysokość ściany bocznej (H).

Przykład 1:

a = 6 cm
h = 4 cm

Obliczamy krawędź boczną (b):

b² = h² + (a²/2) b² = 4² + (6²/2) b² = 16 + (36/2) b² = 16 + 18 b² = 34 b = √34 cm

Obliczamy wysokość ściany bocznej (H):

H² = h² + (a/2)² H² = 4² + (6/2)² H² = 16 + 3² H² = 16 + 9 H² = 25 H = √25 H = 5 cm

Przykład 2:

Załóżmy, że znamy krawędź boczną (b) i krawędź podstawy (a) i chcemy obliczyć wysokość ostrosłupa (h) i wysokość ściany bocznej (H).

a = 8 cm
b = 7 cm

Obliczamy wysokość ostrosłupa (h):

b² = h² + (a²/2) 7² = h² + (8²/2) 49 = h² + (64/2) 49 = h² + 32 h² = 49 - 32 h² = 17 h = √17 cm

Obliczamy wysokość ściany bocznej (H):

H² = b² - (a/2)² H² = 7² - (8/2)² H² = 49 - 4² H² = 49 - 16 H² = 33 H = √33 cm

Przykład 3:

Załóżmy, że znamy wysokość ściany bocznej (H) i krawędź podstawy (a) i chcemy obliczyć wysokość ostrosłupa (h) i krawędź boczną (b).

a = 10 cm
H = 13 cm

Obliczamy wysokość ostrosłupa (h):

H² = h² + (a/2)² 13² = h² + (10/2)² 169 = h² + 5² 169 = h² + 25 h² = 169 - 25 h² = 144 h = √144 h = 12 cm

Obliczamy krawędź boczną (b):

b² = H² + (a/2)² b² = 13² + (10/2)² b² = 169 + 5² b² = 169 + 25 b² = 194 b = √194 cm

Obliczanie Pola Powierzchni i Objętości

Oprócz obliczania długości, istotne jest również zrozumienie, jak obliczyć pole powierzchni i objętość ostrosłupa prawidłowego czworokątnego.

Pole podstawy (Pp): Ponieważ podstawą jest kwadrat, Pp = a²
Pole ściany bocznej (Pb): Każda ściana boczna jest trójkątem równoramiennym, więc Pb = (1/2) * a * H. Ponieważ mamy 4 ściany boczne, pole powierzchni bocznej (Pбок) = 4 * (1/2) * a * H = 2 * a * H
Pole powierzchni całkowitej (Pc): Pc = Pp + Pбок = a² + 2 * a * H
Objętość (V): V = (1/3) * Pp * h = (1/3) * a² * h

Przykład obliczenia pola powierzchni i objętości:

Użyjemy danych z Przykładu 1: a = 6 cm, h = 4 cm, H = 5 cm.

Pole podstawy (Pp):

Pp = a² = 6² = 36 cm²

Pole powierzchni bocznej (Pбок):

Pбок = 2 * a * H = 2 * 6 * 5 = 60 cm²

Pole powierzchni całkowitej (Pc):

Pc = Pp + Pбок = 36 + 60 = 96 cm²

Objętość (V):

V = (1/3) * a² * h = (1/3) * 6² * 4 = (1/3) * 36 * 4 = 12 * 4 = 48 cm³

Obliczanie Kątów

W ostrosłupie prawidłowym czworokątnym możemy również obliczać różne kąty. Najczęściej rozważane są kąty:

Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy (α): Tangens tego kąta jest równy wysokości ostrosłupa (h) podzielonej przez połowę przekątnej podstawy (a√2 / 2). Zatem tan(α) = h / (a√2 / 2) = (2h) / (a√2)
Kąt nachylenia ściany bocznej do płaszczyzny podstawy (β): Tangens tego kąta jest równy wysokości ostrosłupa (h) podzielonej przez połowę krawędzi podstawy (a/2). Zatem tan(β) = h / (a/2) = (2h) / a

Przykład obliczenia kątów:

Użyjemy danych z Przykładu 1: a = 6 cm, h = 4 cm.

Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy (α):

tan(α) = (2h) / (a√2) = (2 * 4) / (6√2) = 8 / (6√2) = 4 / (3√2) = (4√2) / 6 = (2√2) / 3 α = arctan((2√2) / 3)

Kąt nachylenia ściany bocznej do płaszczyzny podstawy (β):

tan(β) = (2h) / a = (2 * 4) / 6 = 8 / 6 = 4 / 3 β = arctan(4/3)

W ten sposób, znając odpowiednie zależności i wzory, możemy obliczyć wszystkie istotne długości, pola, objętości i kąty w ostrosłupie prawidłowym czworokątnym. Pamiętajcie, żeby zawsze dokładnie analizować dane zadania i wybierać odpowiednie wzory do obliczeń. Kluczowe jest również zrozumienie geometrii bryły i zależności między jej elementami.

Pamiętajcie, ćwiczenie czyni mistrza! Im więcej zadań rozwiążecie, tym lepiej zrozumiecie te zagadnienia. Powodzenia!