Pole Trojkata Rownoramiennego Jest Rowne 48

Cześć! Witaj w naszym przewodniku, który pomoże Ci zrozumieć i rozwiązać zadanie: "Pole trójkąta równoramiennego jest równe 48." Brzmi strasznie? Bez obaw! Rozłożymy to na czynniki pierwsze, krok po kroku, żebyś na egzaminie poczuł(a) się pewnie i komfortowo. Zaczynajmy!
Co to jest trójkąt równoramienny?
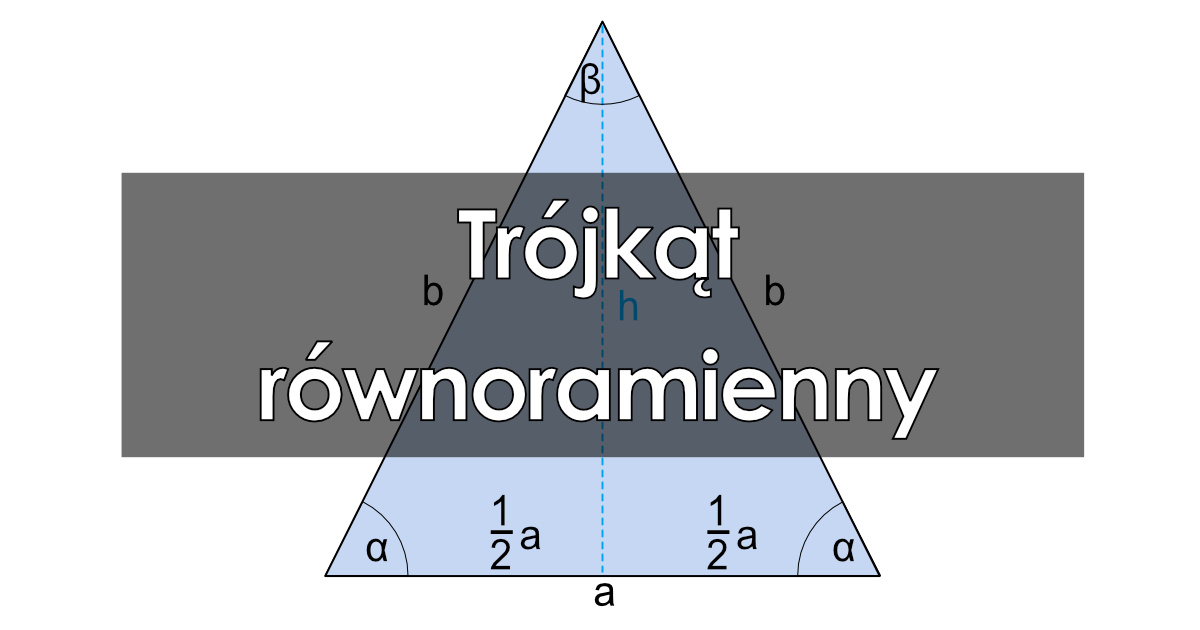
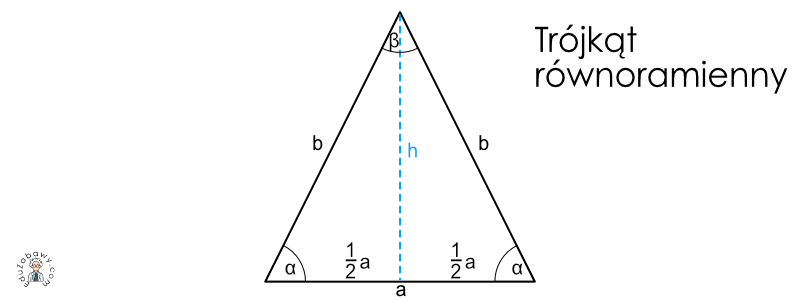
Zanim przejdziemy do konkretnego zadania, upewnijmy się, że rozumiemy podstawowe pojęcia. Trójkąt równoramienny to taki trójkąt, który ma dwa boki równej długości. Te dwa równe boki nazywamy ramionami, a trzeci bok nazywamy podstawą. Kąty przy podstawie w trójkącie równoramiennym są równe. Pamiętaj o tym, bo to bardzo ważne!
Wyobraź sobie trójkąt. Dwa jego boki są dokładnie takie same. To właśnie jest trójkąt równoramienny.
Wzór na pole trójkąta
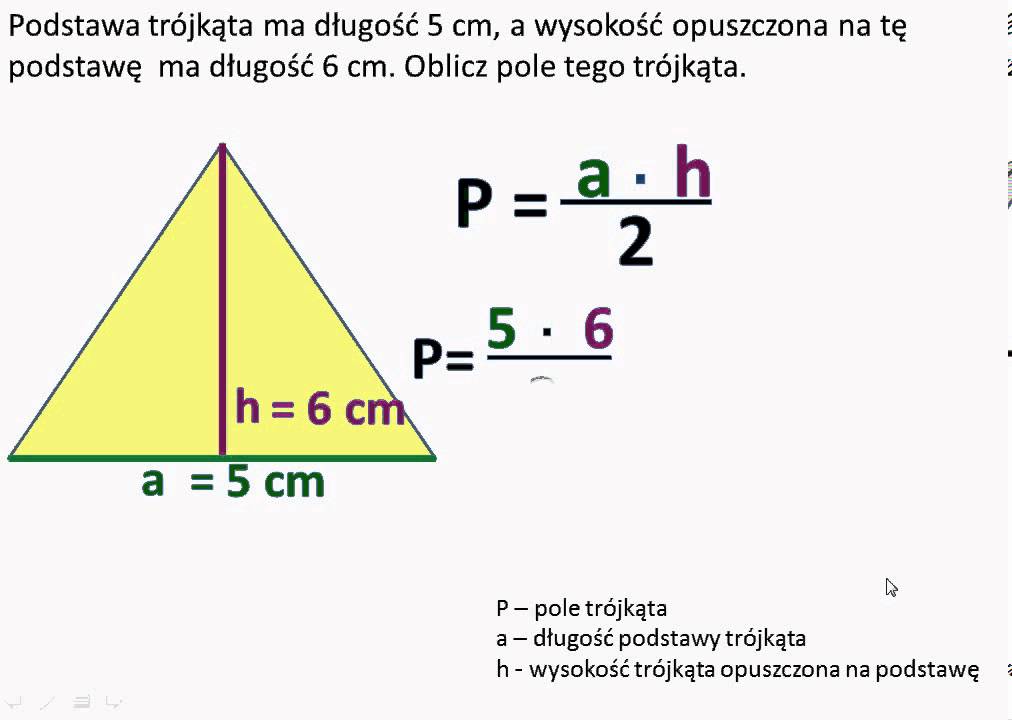
Kolejna kluczowa rzecz to wzór na pole trójkąta. Ogólny wzór brzmi:
Pole = (1/2) * podstawa * wysokość
Czyli:
P = (1/2) * a * h
Gdzie:
- P to pole trójkąta
- a to długość podstawy
- h to wysokość trójkąta (linia prostopadła do podstawy, poprowadzona z wierzchołka naprzeciwległego do tej podstawy).
W przypadku trójkąta równoramiennego, wysokość opuszczona na podstawę dzieli ją na dwie równe części. To ważna właściwość, którą wykorzystamy później.
Rozwiązanie zadania: Pole trójkąta równoramiennego = 48
Teraz przejdźmy do sedna. Mamy informację, że pole trójkąta równoramiennego wynosi 48. Czyli wiemy, że:
P = 48
I musimy znaleźć coś więcej – albo długość podstawy, albo wysokość, albo związek między nimi. Bez dodatkowych informacji nie możemy jednoznacznie określić długości podstawy i wysokości, ponieważ istnieje nieskończenie wiele trójkątów równoramiennych o polu równym 48.
Przykład 1:
Załóżmy, że znamy wysokość. Powiedzmy, że wysokość trójkąta równoramiennego h wynosi 12. Wtedy:
48 = (1/2) * a * 12
Żeby obliczyć długość podstawy (a), musimy przekształcić to równanie:
48 = 6 * a
a = 48 / 6
a = 8
Więc w tym przypadku podstawa trójkąta ma długość 8.
Przykład 2:
A co, jeśli znamy długość podstawy? Załóżmy, że podstawa a wynosi 16. Wtedy:
48 = (1/2) * 16 * h
48 = 8 * h
h = 48 / 8
h = 6
W takim przypadku wysokość trójkąta wynosi 6.
Wniosek: Do rozwiązania zadania potrzebujemy dodatkowej informacji. Samo pole nie wystarczy, żeby jednoznacznie określić wymiary trójkąta równoramiennego.
Zastosowanie Twierdzenia Pitagorasa
Często w zadaniach dotyczących trójkątów równoramiennych pojawia się **Twierdzenie Pitagorasa**. Pamiętaj o nim! Dotyczy ono trójkątów prostokątnych i mówi, że suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.
a2 + b2 = c2
W trójkącie równoramiennym możemy "ukryć" trójkąt prostokątny, rysując wysokość na podstawę. Wtedy ta wysokość dzieli trójkąt równoramienny na dwa identyczne trójkąty prostokątne. Przyprostokątnymi są połowa podstawy oraz wysokość, a przeciwprostokątną jest ramię trójkąta równoramiennego.
Załóżmy, że w naszym zadaniu wiemy dodatkowo, że ramię trójkąta równoramiennego ma długość 10, a pole wynosi 48. Wtedy możemy najpierw obliczyć wysokość (tak jak w Przykładzie 2, zakładając, że znamy podstawę), a potem skorzystać z Twierdzenia Pitagorasa, żeby znaleźć długość połowy podstawy, a następnie całej podstawy.
To właśnie kombinacja wzoru na pole trójkąta i Twierdzenia Pitagorasa daje nam narzędzia do rozwiązywania bardziej skomplikowanych zadań.
Najczęstsze błędy i jak ich unikać
- Zapominanie o połowie w wzorze na pole: Pamiętaj, że pole trójkąta to jedna druga razy podstawa razy wysokość.
- Mylenie podstawy z ramieniem: W trójkącie równoramiennym ważne jest, żeby odróżnić podstawę (bok różnej długości) od ramion (dwa boki o tej samej długości).
- Niezastosowanie Twierdzenia Pitagorasa: Jeśli masz dane dotyczące ramion i wysokości (lub ich relacji), spróbuj wykorzystać Twierdzenie Pitagorasa.
Podsumowanie
Podsumowując:
- Trójkąt równoramienny ma dwa boki równej długości (ramiona) i podstawę.
- Pole trójkąta obliczamy ze wzoru: P = (1/2) * a * h, gdzie a to podstawa, a h to wysokość.
- Do jednoznacznego określenia wymiarów trójkąta równoramiennego o danym polu potrzebujemy dodatkowej informacji (np. długości wysokości, podstawy lub ramienia).
- Twierdzenie Pitagorasa jest bardzo przydatne w rozwiązywaniu zadań dotyczących trójkątów prostokątnych, a więc i trójkątów równoramiennych.
Mam nadzieję, że ten przewodnik pomógł Ci zrozumieć zadanie. Nie bój się ćwiczyć! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz te zagadnienia i tym pewniej poczujesz się na egzaminie. Powodzenia!