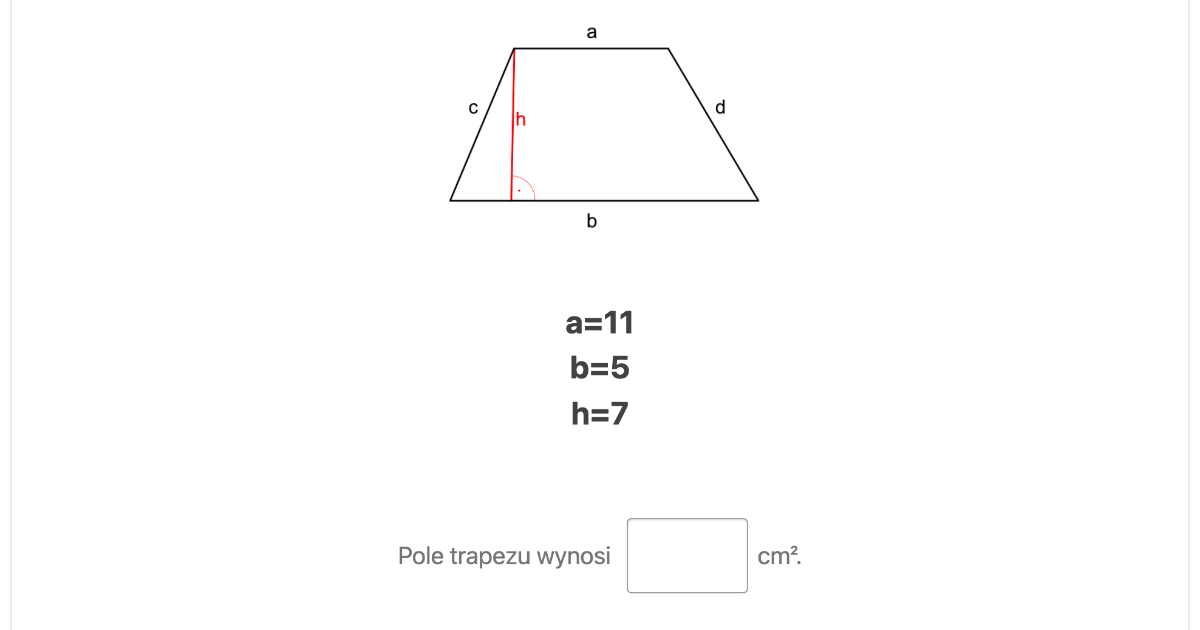
Pole Trapezu Narysowanego Obok Jest Równe

Witaj! Dziś zajmiemy się obliczaniem pola trapezu. Brzmi groźnie? Nic bardziej mylnego! Pomyśl o trapezie jak o figurze, która przypomina przecięty dach domu albo rozciągniętą spódnicę. Zaraz zobaczysz, że obliczanie jego pola jest proste jak 1, 2, 3!

Co to właściwie jest trapez?

Trapez to czworokąt, który ma jedną parę boków równoległych. Te boki równoległe nazywamy podstawami. Jedna z nich jest dłuższa, a druga krótsza (choć zdarzają się trapezy, gdzie są równe – wtedy mamy do czynienia z prostokątem lub kwadratem, które są szczególnymi przypadkami trapezu!). Pozostałe dwa boki nazywamy ramionami. Wyobraź sobie blat stołu – jeśli jeden brzeg jest dłuższy od przeciwległego, a brzeg i przeciwległy brzeg są równoległe, to blat ma kształt trapezu.

Możemy wyróżnić kilka rodzajów trapezów:

• Trapez równoramienny: Ma ramiona równej długości. Wygląda elegancko i symetrycznie!
• Trapez prostokątny: Ma przynajmniej jeden kąt prosty (90 stopni). Jeden z jego ramion jest prostopadły do podstaw.
• Trapez różnoboczny: Nie ma żadnych specjalnych cech – ramiona są różnej długości, a kąty nie są proste.

Bez względu na rodzaj trapezu, zasada obliczania jego pola jest taka sama!

Jak obliczyć pole trapezu?

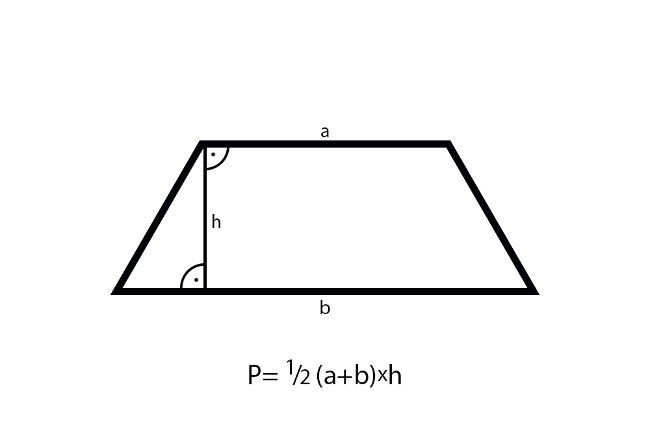
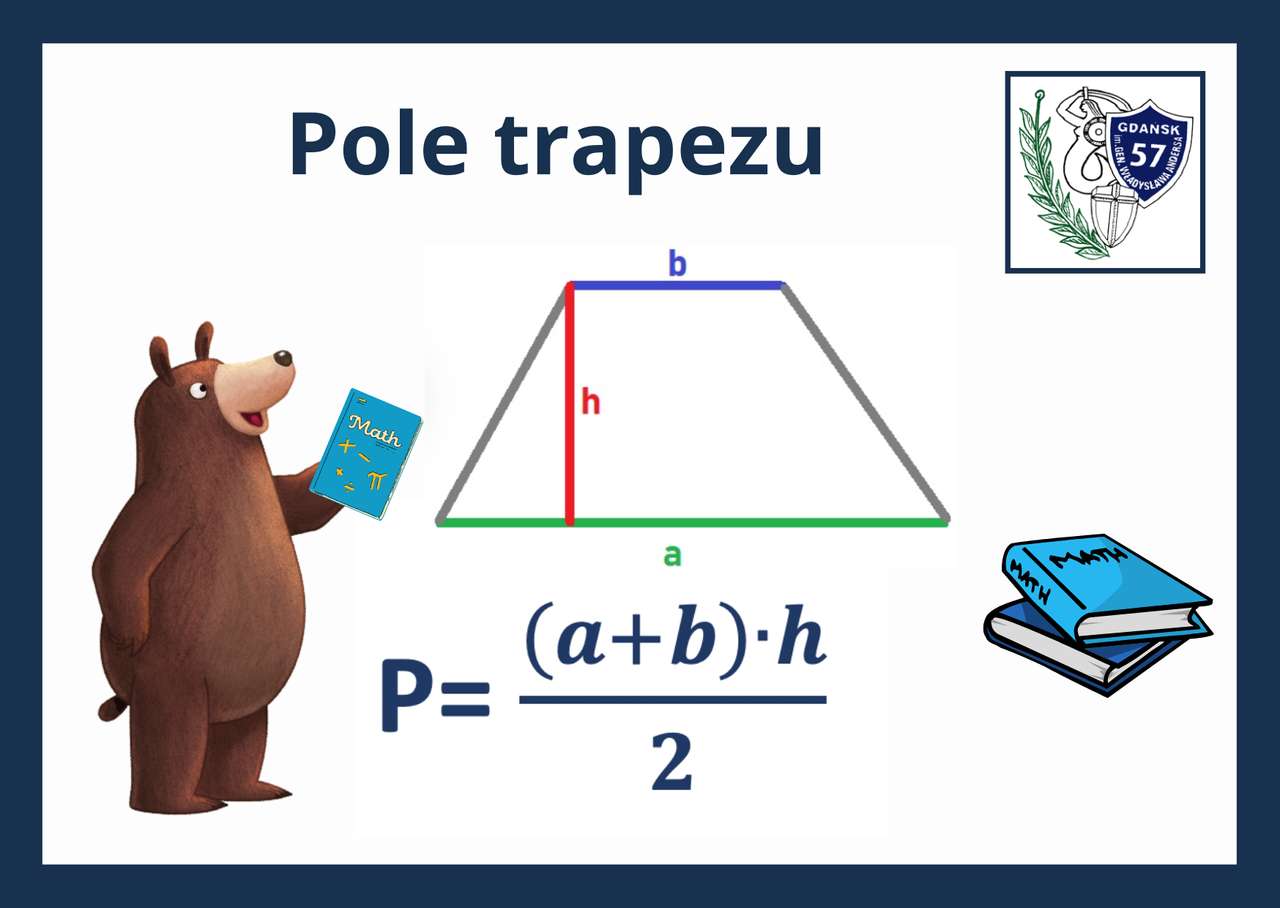
Wzór na pole trapezu wygląda następująco:

P = (a + b) * h / 2

Gdzie:

• P to pole trapezu
• a to długość jednej podstawy
• b to długość drugiej podstawy
• h to wysokość trapezu (odległość między podstawami)

Zauważ, że wysokość zawsze musi być prostopadła do podstaw! Wyobraź sobie, że rysujesz linię prostą od jednej podstawy do drugiej, tak żeby tworzyła z nimi kąt prosty (90 stopni). Ta linia to właśnie wysokość.

Krok po kroku: Obliczanie pola

Żeby obliczyć pole trapezu, wykonaj następujące kroki:

1. Zmierz długość obu podstaw (a i b). Upewnij się, że mierzysz je w tej samej jednostce (np. centymetry, metry).
2. Zmierz wysokość trapezu (h). Pamiętaj, żeby wysokość była prostopadła do podstaw.
3. Dodaj długości podstaw do siebie: (a + b).
4. Pomnóż sumę podstaw przez wysokość: (a + b) * h.
5. Podziel wynik przez 2: ((a + b) * h) / 2.

Voilà! Otrzymałeś pole trapezu!

Dlaczego to działa? Wizualizacja i porównania

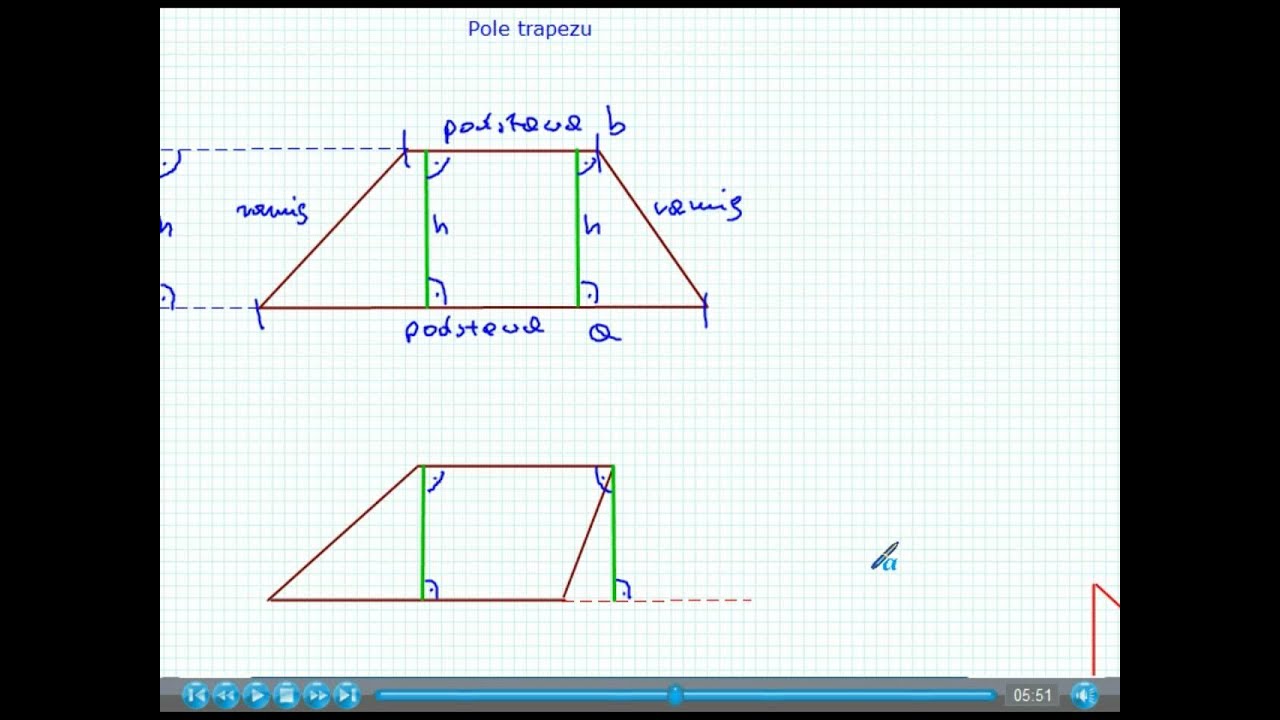
Możesz zastanawiać się, dlaczego akurat taki wzór. Spróbujmy to zrozumieć wizualnie. Wyobraź sobie, że masz trapez. Skopiuj ten trapez i obróć go o 180 stopni. Następnie przyłóż go do oryginalnego trapezu, tak żeby dłuższa podstawa jednego trapezu przylegała do krótszej podstawy drugiego. Co otrzymasz? Równoległobok!

Pole równoległoboku to podstawa razy wysokość. Podstawa tego równoległoboku to suma podstaw trapezu (a + b), a wysokość to wysokość trapezu (h). Więc pole równoległoboku to (a + b) * h. Ale my mieliśmy tylko jeden trapez! Dlatego musimy podzielić pole równoległoboku przez 2. Stąd wzór: P = (a + b) * h / 2.

Inna wizualizacja: Możemy "przeciąć" trapez na pół wzdłuż linii środkowej (linia łącząca środki ramion) i obrócić powstałe części tak, aby utworzyć prostokąt. Długość tego prostokąta będzie równa średniej długości podstaw trapezu ((a+b)/2), a szerokość będzie równa wysokości trapezu (h). Zatem pole prostokąta, a tym samym i trapezu, to ((a+b)/2) * h, co jest tożsame ze wzorem (a + b) * h / 2.

Przykłady z życia wzięte

Gdzie w życiu codziennym możemy spotkać trapezy?

• Dach domu: Jak już wspomnieliśmy, wiele dachów ma kształt trapezu. Obliczając pole dachu, możemy oszacować ilość potrzebnych materiałów budowlanych.
• Torebka: Niektóre torebki mają kształt trapezu. Projektanci torebek muszą znać geometrię, żeby obliczyć ilość materiału potrzebnego do uszycia torebki.
• Przekrój nasypu drogowego: Inżynierowie budowlani wykorzystują obliczenia pól trapezów, aby określić objętość ziemi potrzebnej do budowy nasypów.
• Kawałek pizzy: Choć zwykle pizza jest krojona na trójkąty, czasem możemy dostać kawałek w kształcie trapezu, zwłaszcza jeśli pizza jest prostokątna.

Podsumowanie

Obliczanie pola trapezu nie jest trudne! Pamiętaj o wzorze: P = (a + b) * h / 2. Zmierz długości podstaw, wysokość, dodaj podstawy do siebie, pomnóż przez wysokość i podziel przez dwa. I gotowe! Teraz możesz śmiało obliczać pola trapezów w zadaniach i w życiu codziennym. Powodzenia!