Pole Powierzchni I Objętość Graniastosłupa

Witaj! W tym artykule zgłębimy tajniki obliczania pola powierzchni i objętości graniastosłupa. To podstawowe zagadnienia z geometrii przestrzennej, które przydają się nie tylko w szkole, ale i w wielu praktycznych sytuacjach.

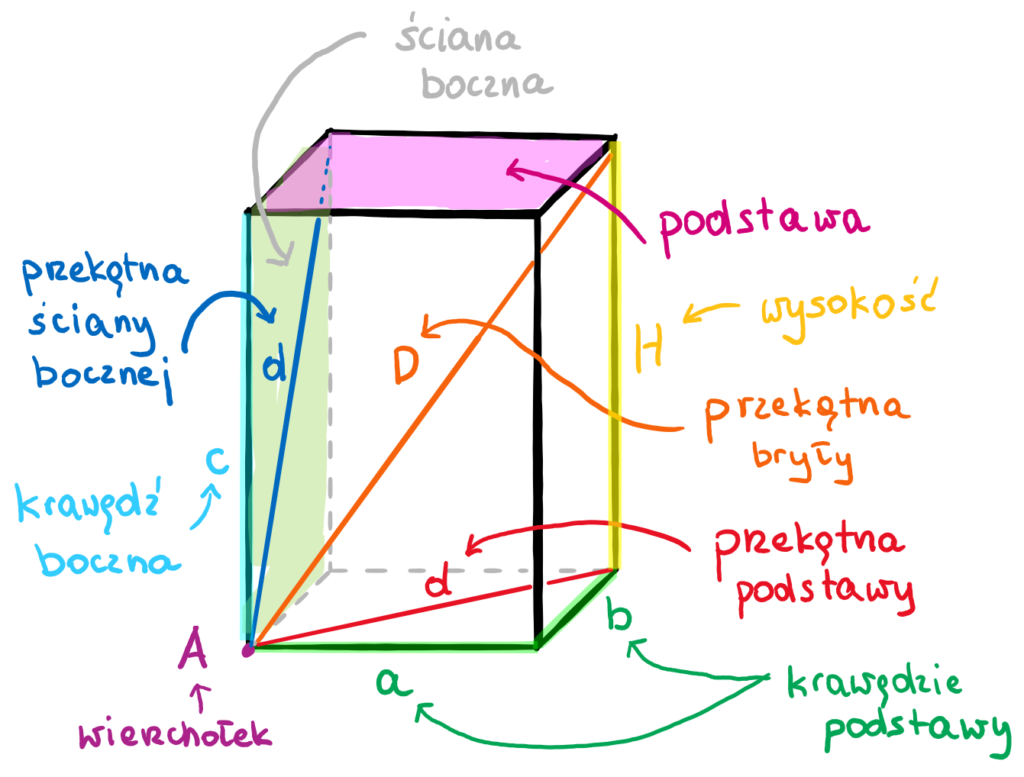
Co to jest graniastosłup?

Zacznijmy od definicji. Graniastosłup to bryła geometryczna, która ma dwie identyczne i równoległe podstawy, połączone ścianami bocznymi będącymi równoległobokami (najczęściej prostokątami). Wyobraź sobie kostkę do gry – to graniastosłup. Typ podstawy decyduje o nazwie graniastosłupa. Mamy więc:

Graniastosłup trójkątny: Jego podstawą jest trójkąt.
Graniastosłup czworokątny: Jego podstawą jest czworokąt (np. kwadrat, prostokąt, równoległobok). Szczególnym przypadkiem jest prostopadłościan, którego wszystkie ściany są prostokątami, oraz sześcian, którego wszystkie ściany są kwadratami.
Graniastosłup pięciokątny: Jego podstawą jest pięciokąt.
Graniastosłup sześciokątny: Jego podstawą jest sześciokąt.
... i tak dalej.

Wyróżniamy także graniastosłupy proste i graniastosłupy pochyłe. W graniastosłupie prostym ściany boczne są prostopadłe do podstaw. W graniastosłupie pochyłym ściany boczne nie są prostopadłe do podstaw. W tym artykule skupimy się głównie na graniastosłupach prostych, gdyż są one częściej spotykane w zadaniach i praktyce.

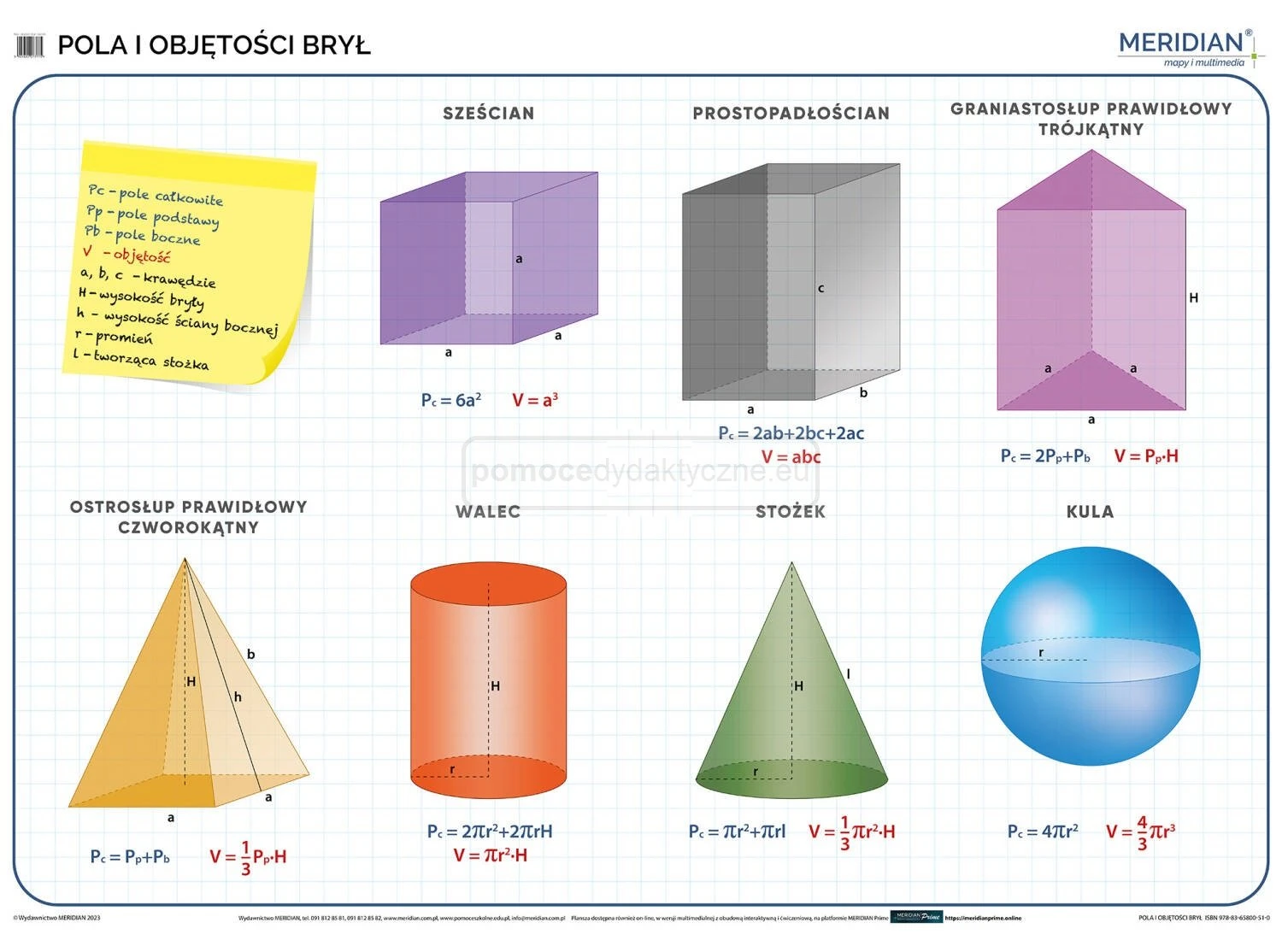
Pole Powierzchni Graniastosłupa

Pole powierzchni graniastosłupa to suma pól wszystkich jego ścian. Składa się ono z dwóch pól podstaw (bo mamy dwie identyczne podstawy) oraz pól ścian bocznych.

Wzór na pole powierzchni całkowitej

Ogólny wzór na pole powierzchni całkowitej (Pc) graniastosłupa prostego to:

Pc = 2 * Pp + Pb

Gdzie:

Pc to pole powierzchni całkowitej.
Pp to pole jednej podstawy.
Pb to pole powierzchni bocznej (suma pól wszystkich ścian bocznych).

Jak obliczyć pole podstawy (Pp)?

Sposób obliczenia pola podstawy zależy od kształtu podstawy. Przypomnijmy sobie wzory na pola kilku podstawowych figur:

Trójkąt: Pp = (a * h) / 2, gdzie a to długość podstawy trójkąta, a h to wysokość trójkąta opuszczona na tę podstawę.
Kwadrat: Pp = a², gdzie a to długość boku kwadratu.
Prostokąt: Pp = a * b, gdzie a i b to długości boków prostokąta.
Równoległobok: Pp = a * h, gdzie a to długość podstawy równoległoboku, a h to wysokość opuszczona na tę podstawę.
Trapez: Pp = ((a + b) * h) / 2, gdzie a i b to długości podstaw trapezu, a h to wysokość trapezu.

Jak obliczyć pole powierzchni bocznej (Pb)?

Pole powierzchni bocznej graniastosłupa prostego to suma pól wszystkich jego ścian bocznych. Ściany boczne są zazwyczaj prostokątami, a ich pole obliczamy jako a * h, gdzie a to długość boku prostokąta (czyli krawędź podstawy), a h to wysokość graniastosłupa.

Bardzo ważna obserwacja: Pole powierzchni bocznej graniastosłupa prostego można obliczyć także jako obwód podstawy (Obw) pomnożony przez wysokość graniastosłupa (H):

Pb = Obw * H

To znacząco upraszcza obliczenia, szczególnie gdy podstawa ma wiele boków.

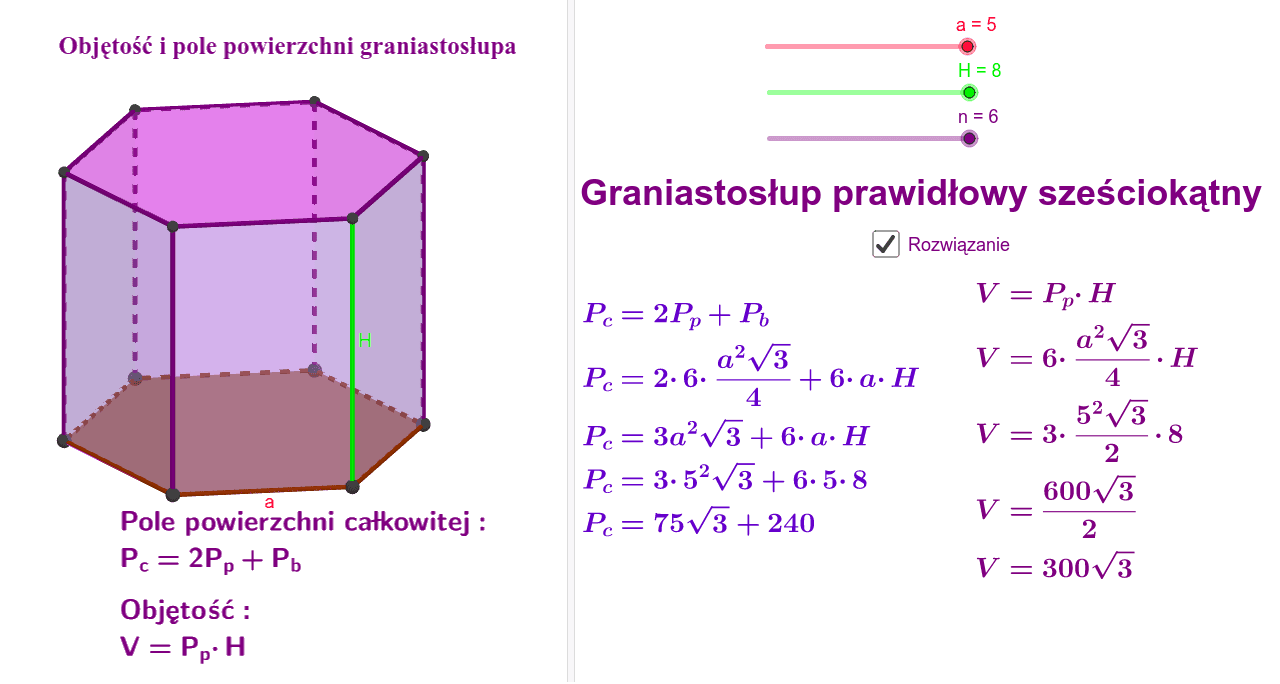
Objętość Graniastosłupa

Objętość graniastosłupa to ilość przestrzeni, jaką zajmuje ta bryła.

Wzór na objętość

Wzór na objętość (V) graniastosłupa jest bardzo prosty:

V = Pp * H

Gdzie:

V to objętość.
Pp to pole podstawy.
H to wysokość graniastosłupa.

Zauważ, że do obliczenia objętości potrzebujemy tylko pola podstawy i wysokości! Niezależnie od tego, czy graniastosłup jest trójkątny, czworokątny, czy ma jeszcze inną podstawę, wzór jest ten sam.

Przykłady

Przykład 1: Graniastosłup prawidłowy czworokątny (prostopadłościan)

Mamy prostopadłościan o wymiarach: a = 3 cm, b = 4 cm, H = 5 cm.

Pp = a * b = 3 cm * 4 cm = 12 cm²

Pb = 2 * (a * H) + 2 * (b * H) = 2 * (3 cm * 5 cm) + 2 * (4 cm * 5 cm) = 30 cm² + 40 cm² = 70 cm²

Pc = 2 * Pp + Pb = 2 * 12 cm² + 70 cm² = 24 cm² + 70 cm² = 94 cm²

V = Pp * H = 12 cm² * 5 cm = 60 cm³

Przykład 2: Graniastosłup trójkątny prosty

Podstawa to trójkąt prostokątny o bokach: a = 5 cm, b = 12 cm (przyprostokątne), H = 10 cm (wysokość graniastosłupa).

Pp = (a * b) / 2 = (5 cm * 12 cm) / 2 = 30 cm²

Do obliczenia Pb potrzebujemy obwodu podstawy. Musimy obliczyć przeciwprostokątną (c) trójkąta z twierdzenia Pitagorasa: c² = a² + b² = 5² + 12² = 25 + 144 = 169 => c = 13 cm.

Obw = a + b + c = 5 cm + 12 cm + 13 cm = 30 cm

Pb = Obw * H = 30 cm * 10 cm = 300 cm²

Pc = 2 * Pp + Pb = 2 * 30 cm² + 300 cm² = 60 cm² + 300 cm² = 360 cm²

V = Pp * H = 30 cm² * 10 cm = 300 cm³

Zastosowania praktyczne

Wiedza o polu powierzchni i objętości graniastosłupów jest przydatna w wielu dziedzinach, na przykład:

Budownictwo: Obliczanie ilości materiałów potrzebnych do budowy ścian, dachów, itp.
Projektowanie opakowań: Określanie wymiarów pudełek, kontenerów, aby zmieścić określoną ilość produktu.
Inżynieria: Projektowanie mostów, tuneli i innych konstrukcji.
Architektura: Planowanie przestrzeni w budynkach, obliczanie powierzchni pomieszczeń.

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, jak obliczać pole powierzchni i objętość graniastosłupa. Pamiętaj, że kluczem do sukcesu jest zrozumienie definicji i wzorów, a następnie ćwiczenie na przykładach. Powodzenia!