Pole Kwadratu Z Przekątnej Wzór

Zapewne nie raz spotkałeś się z problemem obliczenia pola kwadratu, mając daną jedynie długość jego przekątnej. Może to być zadanie szkolne, element projektu architektonicznego, a nawet wyzwanie związane z majsterkowaniem. Niezależnie od powodu, zrozumienie jak to zrobić jest niezwykle przydatne. Na szczęście, istnieje prosty i elegancki wzór, który pozwala szybko rozwiązać ten problem. Ten artykuł pomoże Ci go zrozumieć i skutecznie wykorzystać.

Rozważmy sytuację: Masz kwadrat, ale nie znasz długości jego boków. Jedyne, co wiesz, to długość linii, która łączy przeciwległe wierzchołki – przekątnej. Jak w takiej sytuacji obliczyć pole tego kwadratu? Brzmi to jak trudne zadanie, ale w rzeczywistości jest to prostsze niż myślisz!

Dlaczego to ważne? Zastosowania w życiu codziennym.

Zanim przejdziemy do wzoru, warto zrozumieć, dlaczego ta wiedza może być przydatna. W rzeczywistości, obliczanie pola kwadratu z przekątnej znajduje zastosowanie w wielu dziedzinach:

• Architektura i budownictwo: Planowanie przestrzeni, obliczanie powierzchni podłóg, dachów, okien.
• Projektowanie wnętrz: Określanie ilości materiałów potrzebnych do wykończenia (np. płytek, paneli).
• Grafika i projektowanie: Obliczenia związane z tworzeniem logo, banerów, układów graficznych.
• Matematyka i fizyka: Rozwiązywanie problemów geometrycznych i obliczeniowych.
• Majsterkowanie: Planowanie projektów DIY, np. budowa ramek, półek, elementów dekoracyjnych.

Wyobraź sobie, że projektujesz ogródek i masz dostępny obszar w kształcie kwadratu, którego przekątną zmierzyłeś. Znając długość przekątnej, możesz precyzyjnie obliczyć powierzchnię, którą masz do dyspozycji, i zaplanować nasadzenia.

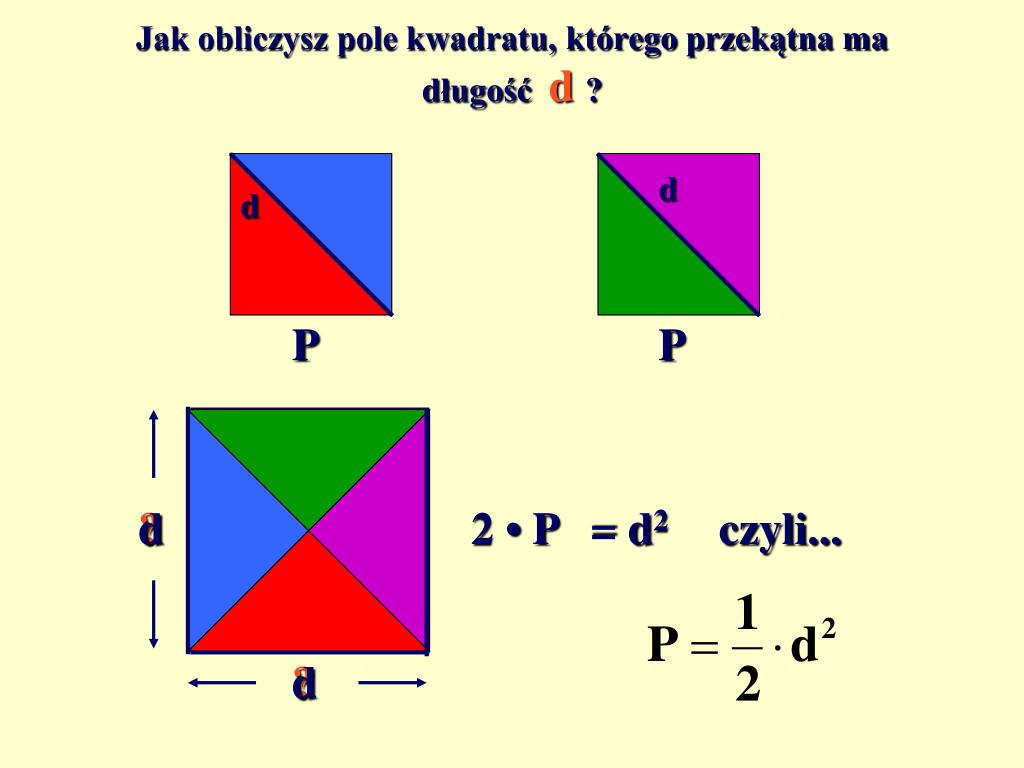
Wzór na pole kwadratu z przekątnej

Kluczem do rozwiązania tego problemu jest wzór, który łączy długość przekątnej z polem kwadratu. Brzmi on następująco:

Pole kwadratu (P) = (d²) / 2

Gdzie:

• P oznacza pole kwadratu.
• d oznacza długość przekątnej.

Ten wzór jest prosty, elegancki i bardzo skuteczny. Ale skąd się on bierze? Wyjaśnimy to krok po kroku.

Dowód wzoru – zrozumienie, a nie tylko zapamiętanie

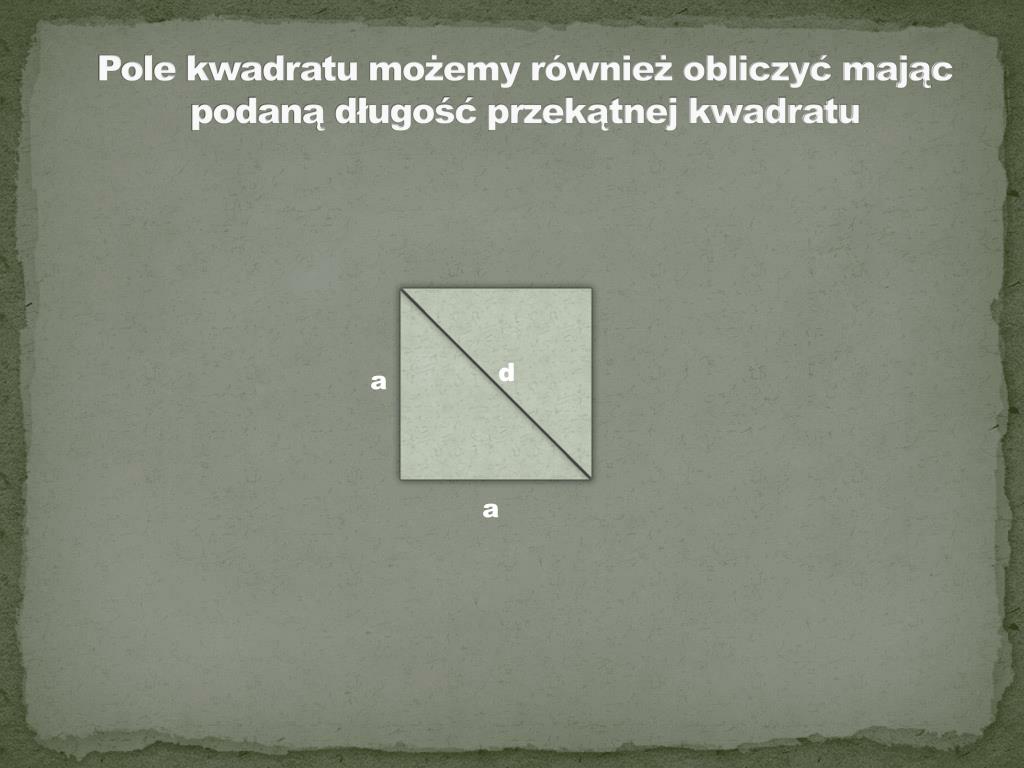
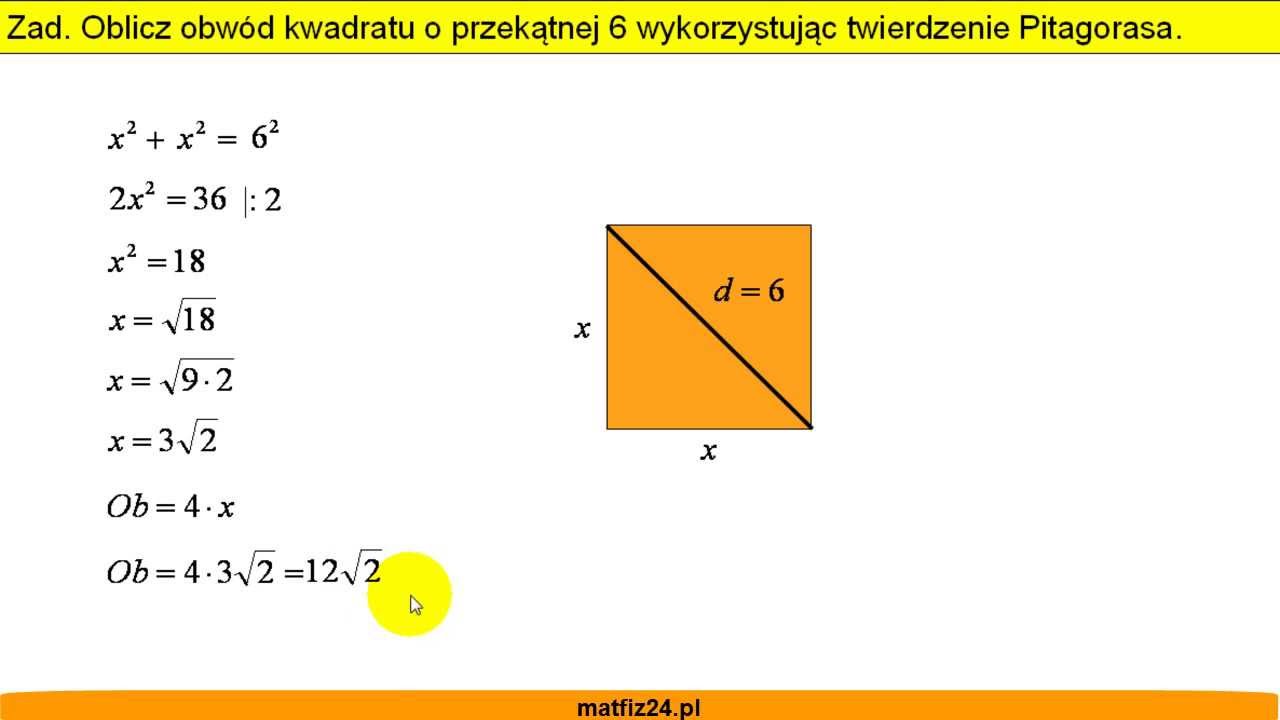
Wzór na pole kwadratu z przekątnej można wyprowadzić z twierdzenia Pitagorasa. Pamiętasz, twierdzenie Pitagorasa? Mówi ono, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych (a i b) jest równa kwadratowi długości przeciwprostokątnej (c):

a² + b² = c²

W kwadracie przekątna dzieli go na dwa identyczne trójkąty prostokątne. Przyprostokątne w tych trójkątach to boki kwadratu (a), a przeciwprostokątna to przekątna (d).

Zatem, możemy zapisać:

a² + a² = d²

Upraszczając:

2a² = d²

Teraz podzielimy obie strony równania przez 2:

a² = d² / 2

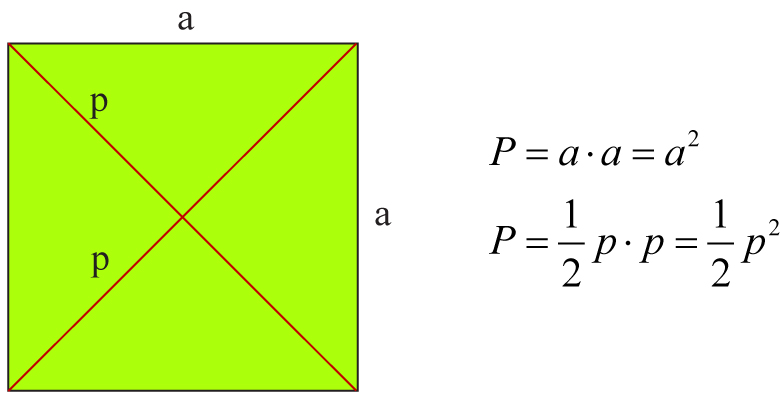
Wiemy, że pole kwadratu (P) to kwadrat jego boku (a²):

P = a²

Zatem:

P = d² / 2

I w ten sposób udowodniliśmy wzór na pole kwadratu z przekątnej! Rozumienie dowodu pomaga zapamiętać wzór i używać go bardziej świadomie.

Przykład użycia – krok po kroku

Załóżmy, że mamy kwadrat, którego przekątna ma długość 10 cm. Jak obliczyć jego pole?

1. Zapisz wzór: P = (d²) / 2
2. Podstaw wartość przekątnej: d = 10 cm
3. Oblicz kwadrat przekątnej: d² = 10² = 100 cm²
4. Podziel kwadrat przekątnej przez 2: P = 100 cm² / 2 = 50 cm²

Odpowiedź: Pole kwadratu wynosi 50 cm².

Częste błędy i jak ich unikać

Podczas obliczania pola kwadratu z przekątnej, można popełnić kilka typowych błędów:

• Zapomnienie o podzieleniu przez 2: Pamiętaj, że wzór to (d²) / 2, a nie tylko d².
• Pomylenie jednostek: Upewnij się, że używasz spójnych jednostek (np. cm i cm²).
• Błędne obliczenie kwadratu liczby: Uważaj przy podnoszeniu przekątnej do kwadratu.

Aby uniknąć błędów, zawsze sprawdzaj swoje obliczenia i upewnij się, że dobrze rozumiesz wzór.

Przeciwdziałanie – Alternatywne metody i argumenty

Może ktoś argumentować, że łatwiej jest znaleźć długość boku kwadratu, mając przekątną, a następnie obliczyć pole jako bok pomnożony przez bok (a²). Jest to prawda, i można to zrobić używając twierdzenia Pitagorasa: a = d / √2. Jednak użycie wzoru P = (d²) / 2 jest bezpośrednie i eliminuje potrzebę obliczania pierwiastka kwadratowego, co może być korzystne w sytuacjach, gdzie liczymy "w głowie" lub gdy kalkulator nie jest pod ręką.

Kolejnym argumentem może być to, że wzór jest trudny do zapamiętania. Jednak, jak pokazaliśmy wcześniej, wzór można łatwo wyprowadzić z twierdzenia Pitagorasa, co ułatwia jego zrozumienie i zapamiętanie. Ponadto, jest to na tyle powszechne zagadnienie w geometrii, że warto go znać.

Rozwiązywanie problemów – praktyczne ćwiczenia

Aby utrwalić wiedzę, spróbuj rozwiązać kilka zadań:

1. Oblicz pole kwadratu, którego przekątna ma długość 7 cm.
2. Znajdź pole kwadratu, którego przekątna ma długość 12,5 cm.
3. Jaka jest powierzchnia kwadratowej serwetki, jeśli jej przekątna mierzy 30 cm?

Rozwiązując te zadania, nabierzesz wprawy w stosowaniu wzoru i zwiększysz swoją pewność siebie.

Podsumowanie i perspektywy

Jak widzisz, obliczanie pola kwadratu z przekątnej jest prostym i przydatnym umiejętnością. Znajomość odpowiedniego wzoru pozwala szybko i sprawnie rozwiązywać problemy geometryczne, które pojawiają się w różnych dziedzinach życia. Wzór P = (d²) / 2 to Twój nowy sprzymierzeniec w świecie geometrii!

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć i zapamiętać wzór na pole kwadratu z przekątnej. Teraz, kiedy już wiesz, jak to zrobić, możesz śmiało wykorzystać tę wiedzę w praktyce. Pamiętaj, że kluczem do sukcesu jest regularne ćwiczenie i stosowanie wzoru w różnych sytuacjach.

Czy jest jakiś konkretny problem geometryczny, który chciałbyś, abym pomógł Ci rozwiązać? A może masz jakieś pytania dotyczące tego wzoru? Daj znać!