Pole Kwadratu Wzór Z Przekątną

Czy kiedykolwiek zastanawiałeś się, jak szybko obliczyć pole kwadratu, mając jedynie długość jego przekątnej? Zapomnij o mozolnym mierzeniu boków! Istnieje elegancki i prosty wzór, który pozwala na błyskawiczne rozwiązanie tego problemu. Ten artykuł jest skierowany do uczniów, studentów, inżynierów, a także wszystkich, którzy pragną poszerzyć swoją wiedzę z zakresu geometrii i szukają sprytnych trików matematycznych. Przygotuj się na podróż w świat kwadratów i ich przekątnych, gdzie odkryjemy potęgę jednego, wyjątkowego wzoru.

Wprowadzenie do kwadratu i jego własności

Zacznijmy od podstaw. Kwadrat to czworokąt foremny, co oznacza, że posiada cztery równe boki i cztery kąty proste (90 stopni). Jest to figura bardzo symetryczna i regularna, co sprawia, że jego właściwości są stosunkowo łatwe do zrozumienia i wykorzystania.

• Boki: Wszystkie cztery boki kwadratu są równe długości. Oznaczamy je zazwyczaj literą 'a'.
• Kąty: Każdy z czterech kątów wewnętrznych kwadratu ma miarę 90 stopni.
• Przekątne: Kwadrat posiada dwie przekątne, które przecinają się pod kątem prostym w połowie swojej długości. Przekątne są również równe sobie.

Przekątna kwadratu - klucz do rozwiązania

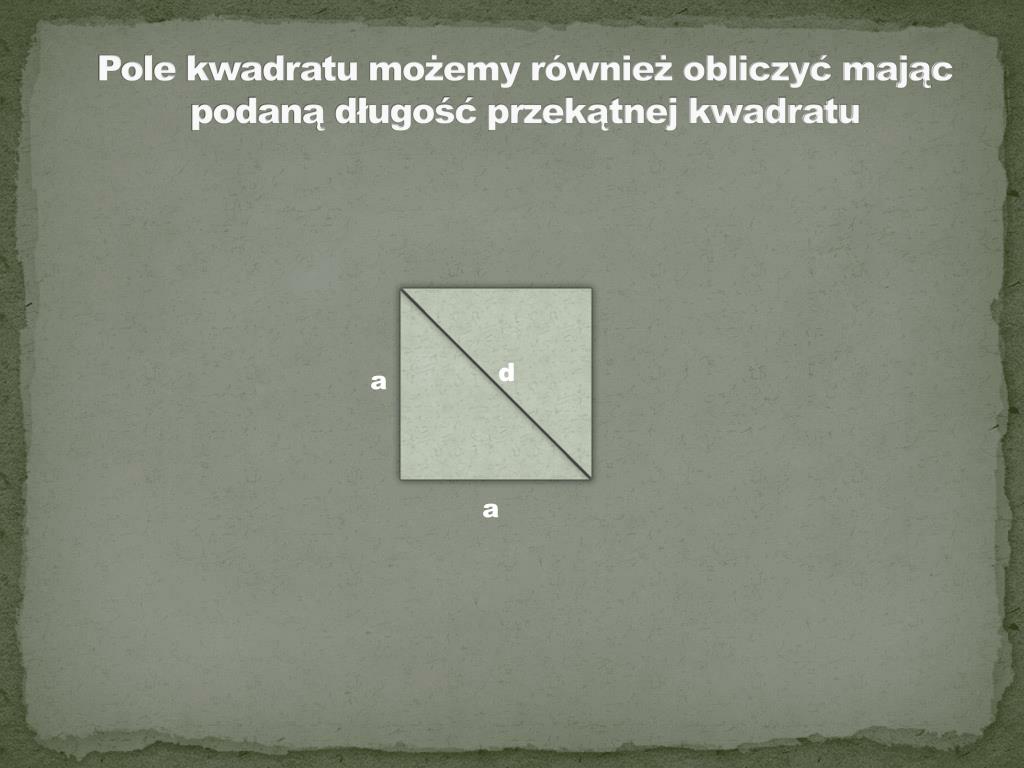
Przekątna kwadratu to odcinek łączący dwa przeciwległe wierzchołki. Ma ona kluczowe znaczenie, ponieważ łączy ze sobą długość boku i pole kwadratu. Zauważmy, że przekątna dzieli kwadrat na dwa trójkąty prostokątne równoramienne. Możemy więc zastosować twierdzenie Pitagorasa do znalezienia zależności między długością boku (a) i długością przekątnej (d).

Z twierdzenia Pitagorasa wynika, że:

a² + a² = d²

2a² = d²

a² = d² / 2

a = √(d² / 2) = d / √2

Wzór na pole kwadratu z użyciem przekątnej

Pole kwadratu (P) możemy obliczyć, mnożąc długość boku przez siebie:

P = a²

Skoro wiemy, że a² = d² / 2, możemy bezpośrednio podstawić to do wzoru na pole:

P = d² / 2

I to jest właśnie ten magiczny wzór! Aby obliczyć pole kwadratu, wystarczy podnieść długość przekątnej do kwadratu i podzielić wynik przez 2. Proste, prawda?

Przykłady zastosowania wzoru

Zobaczmy, jak ten wzór działa w praktyce:

• Przykład 1: Załóżmy, że przekątna kwadratu ma długość 6 cm. Wtedy pole kwadratu wynosi: P = (6 cm)² / 2 = 36 cm² / 2 = 18 cm².
• Przykład 2: Mamy kwadrat, którego przekątna ma długość 10 metrów. Obliczamy pole: P = (10 m)² / 2 = 100 m² / 2 = 50 m².
• Przykład 3: Przekątna placu zabaw w kształcie kwadratu ma długość 14 metrów. Ile metrów kwadratowych ma ten plac? P = (14 m)² / 2 = 196 m² / 2 = 98 m².

Porównanie z tradycyjnym wzorem na pole kwadratu

Tradycyjny wzór na pole kwadratu, jak już wspomnieliśmy, to P = a². Aby go użyć, musimy znać długość boku kwadratu. W sytuacji, gdy znamy tylko długość przekątnej, użycie wzoru P = d² / 2 jest znacznie szybsze i wygodniejsze, ponieważ nie wymaga obliczania długości boku za pomocą twierdzenia Pitagorasa.

Wyobraź sobie sytuację, że musisz szybko obliczyć pole terenu w kształcie kwadratu, a masz do dyspozycji tylko pomiar długości przekątnej. W takim przypadku wzór P = d² / 2 staje się niezastąpiony.

Kiedy warto używać wzoru P = d² / 2?

Wzór ten jest szczególnie przydatny w następujących sytuacjach:

• Gdy znamy tylko długość przekątnej kwadratu. Jest to najbardziej oczywisty przypadek, w którym użycie tego wzoru jest najefektywniejsze.
• W zadaniach, w których długość przekątnej jest podana bezpośrednio lub można ją łatwo obliczyć. Czasami w treści zadania podana jest długość przekątnej, a czasami trzeba ją wyliczyć z innych danych. W obu przypadkach wzór P = d² / 2 upraszcza rozwiązanie.
• W sytuacjach praktycznych, gdy pomiar przekątnej jest łatwiejszy niż pomiar boku. Na przykład, mierząc pole działki w kształcie kwadratu, łatwiej może być zmierzyć przekątną, niż przebiegać wzdłuż boków.

Praktyczne zastosowania w życiu codziennym i zawodowym

Wzór na pole kwadratu z przekątną znajduje zastosowanie w wielu dziedzinach życia i zawodach. Oto kilka przykładów:

• Architektura i budownictwo: Obliczanie powierzchni podłóg, ścian, dachów o kształcie kwadratu.
• Geodezja i kartografia: Obliczanie powierzchni działek, pól, obszarów o kształcie zbliżonym do kwadratu.
• Projektowanie wnętrz: Określanie ilości materiałów potrzebnych do wyłożenia podłogi kwadratowymi płytkami.
• Informatyka: Obliczanie rozmiarów ekranów i okien w aplikacjach.
• Matematyka i fizyka: Rozwiązywanie problemów geometrycznych i fizycznych związanych z kwadratami.

Alternatywne metody obliczania pola kwadratu

Oprócz wzoru z przekątną i wzoru P = a², istnieją również inne, mniej popularne metody obliczania pola kwadratu. Jedną z nich jest wykorzystanie promienia okręgu wpisanego (r) lub opisanego (R) na kwadracie.

• Pole kwadratu z promieniem okręgu wpisanego: P = 4r²
• Pole kwadratu z promieniem okręgu opisanego: P = 2R²

Metody te są jednak mniej bezpośrednie i zazwyczaj wymagają dodatkowych obliczeń, aby znaleźć promień okręgu.

Podsumowanie i korzyści z opanowania wzoru P = d² / 2

Poznaliśmy wzór P = d² / 2, który pozwala na szybkie i efektywne obliczenie pola kwadratu, gdy znamy jedynie długość jego przekątnej. Wzór ten jest prosty w użyciu i znajduje zastosowanie w wielu dziedzinach życia.

Opanowanie tego wzoru przynosi wiele korzyści:

• Oszczędność czasu: Szybkie obliczanie pola bez konieczności mierzenia boków.
• Wygoda: Użycie tylko jednej wartości (długości przekątnej) do obliczeń.
• Wszechstronność: Zastosowanie w różnych dziedzinach życia i zawodach.
• Pewność siebie: Świadomość, że potrafisz rozwiązać problem geometryczny w prosty i elegancki sposób.

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć i docenić potęgę wzoru na pole kwadratu z przekątną. Pamiętaj, że matematyka to nie tylko liczby i wzory, ale także sposób myślenia i rozwiązywania problemów. Im więcej znasz trików i technik, tym łatwiej poradzisz sobie z wyzwaniami, które stawia przed Tobą życie.

Teraz, uzbrojony w nową wiedzę, śmiało ruszaj do rozwiązywania zadań i praktycznego zastosowania wzoru P = d² / 2! Powodzenia!