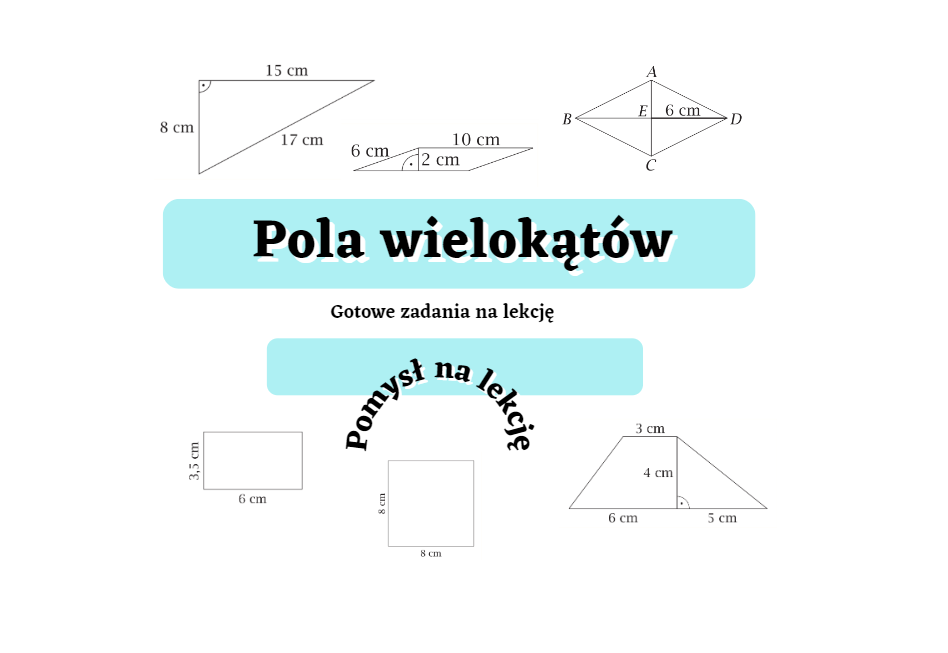
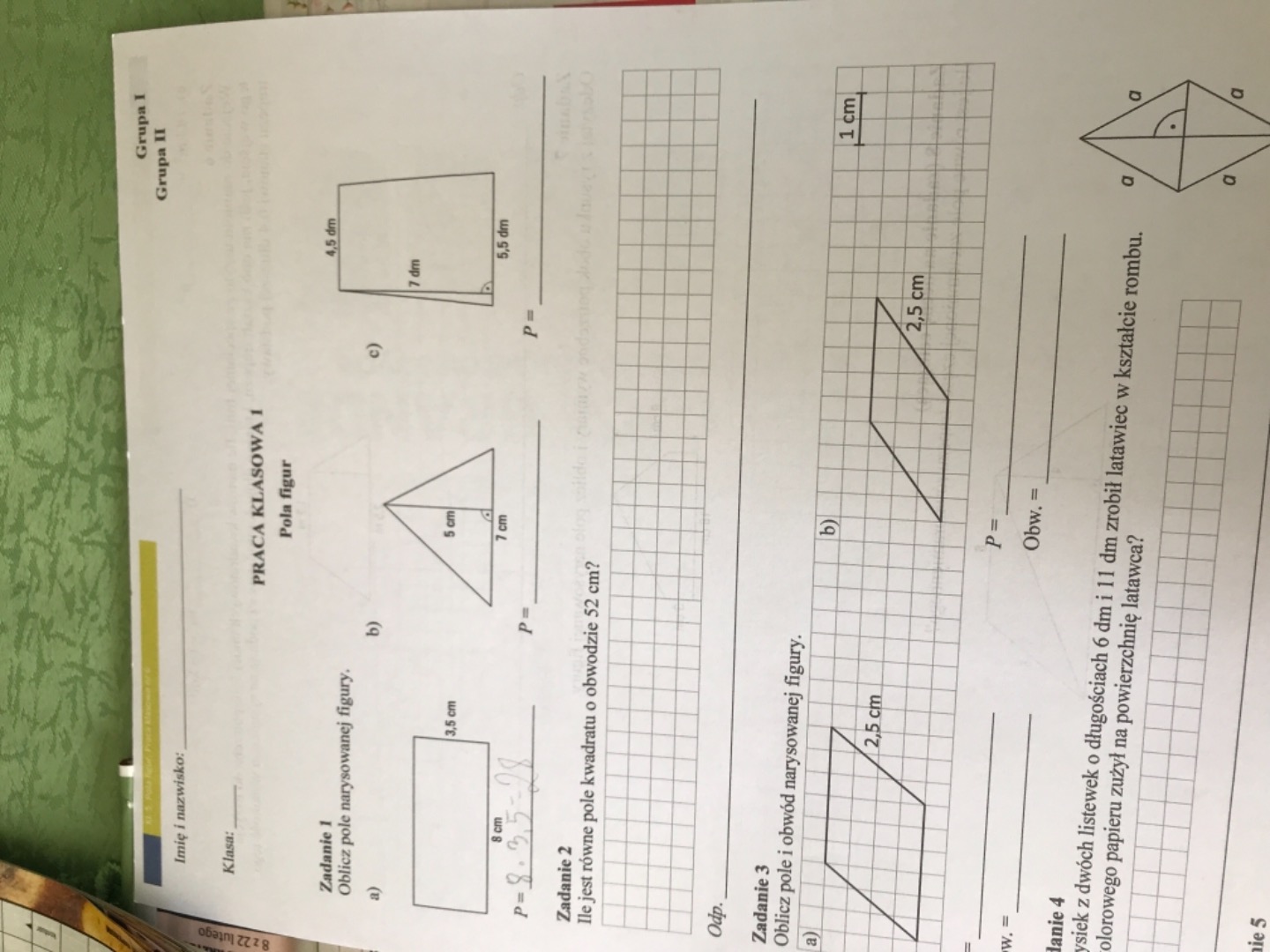
Pola Wielokątów Sprawdzian Klasa 6

Geometria to fascynujący dział matematyki, który towarzyszy nam na każdym kroku. Szczególnie ważna w klasie 6 staje się umiejętność rozumienia i obliczania pól wielokątów. Przygotowanie do sprawdzianu z tego zakresu wymaga solidnej wiedzy teoretycznej i praktycznych umiejętności. Ten artykuł ma na celu kompleksowe przygotowanie uczniów do tego wyzwania.

Podstawowe Definicje i Pojęcia

Zanim przejdziemy do obliczania pól, musimy upewnić się, że doskonale rozumiemy podstawowe definicje. Wielokąt to figura geometryczna, która jest ograniczona linią łamaną zamkniętą. Każdy wielokąt ma swoje wierzchołki (punkty, w których łączą się boki) i boki (odcinki łączące wierzchołki). W klasie 6 najczęściej spotykamy się z trójkątami, kwadratami, prostokątami, równoległobokami, rombami i trapezami.

Rodzaje Wielokątów

Warto znać różnice między poszczególnymi rodzajami wielokątów:

Trójkąt: Wielokąt o trzech bokach i trzech wierzchołkach. Może być równoboczny (wszystkie boki równe), równoramienny (dwa boki równe) lub różnoboczny (wszystkie boki różnej długości).
Kwadrat: Czworokąt o wszystkich bokach równych i wszystkich kątach prostych.
Prostokąt: Czworokąt o kątach prostych, ale niekoniecznie o wszystkich bokach równych.
Równoległobok: Czworokąt, w którym przeciwległe boki są równoległe i równe.
Romb: Równoległobok, który ma wszystkie boki równe.
Trapez: Czworokąt, który ma co najmniej jedną parę boków równoległych.

Znajomość tych definicji jest kluczowa do zrozumienia wzorów na pola i ich prawidłowego stosowania.

Wzory na Pola Wielokątów

Przejdźmy teraz do najważniejszej części – wzorów na pola wielokątów. Należy je zapamiętać i umieć zastosować w praktyce. To absolutna podstawa do zdania sprawdzianu!

Pole Trójkąta

Podstawowy wzór na pole trójkąta to:

P = (a * h) / 2

Gdzie:

P to pole trójkąta
a to długość podstawy trójkąta
h to wysokość trójkąta opuszczona na tę podstawę

Pamiętaj, że wysokość trójkąta musi być prostopadła do podstawy. W przypadku trójkątów ostrokątnych wysokość znajduje się wewnątrz trójkąta, w przypadku trójkątów prostokątnych jedną z wysokości jest przyprostokątna, a w przypadku trójkątów rozwartokątnych wysokość znajduje się poza trójkątem (trzeba przedłużyć podstawę).

Pole Kwadratu

Pole kwadratu obliczamy bardzo prosto:

P = a²

Gdzie:

P to pole kwadratu
a to długość boku kwadratu

Kwadrat jest szczególnym przypadkiem prostokąta, więc można również zastosować wzór na pole prostokąta, ale wzór P = a² jest znacznie szybszy.

Pole Prostokąta

Pole prostokąta obliczamy mnożąc długość jednego boku przez długość drugiego boku:

P = a * b

Gdzie:

P to pole prostokąta
a to długość jednego boku prostokąta
b to długość drugiego boku prostokąta

Pole Równoległoboku

Pole równoległoboku obliczamy podobnie jak pole prostokąta, ale trzeba pamiętać o wysokości:

P = a * h

Gdzie:

P to pole równoległoboku
a to długość podstawy równoległoboku
h to wysokość równoległoboku opuszczona na tę podstawę

Wysokość musi być prostopadła do podstawy, a nie jest nią bok równoległoboku (chyba że równoległobok jest prostokątem).

Pole Rombu

Pole rombu można obliczyć na dwa sposoby:

P = a * h (podobnie jak dla równoległoboku)
P = (d₁ * d₂) / 2 (gdzie d₁ i d₂ to długości przekątnych rombu)

Wybór wzoru zależy od tego, jakie dane mamy podane w zadaniu. Jeśli znamy długość boku i wysokość, używamy pierwszego wzoru. Jeśli znamy długości przekątnych, używamy drugiego wzoru. Oba wzory są poprawne!

Pole Trapezu

Pole trapezu obliczamy za pomocą wzoru:

P = ((a + b) * h) / 2

Gdzie:

P to pole trapezu
a i b to długości podstaw trapezu (boki równoległe)
h to wysokość trapezu (odległość między podstawami)

W trapezie ważne jest, aby prawidłowo zidentyfikować podstawy i wysokość. Wysokość musi być prostopadła do obu podstaw.

Praktyczne Przykłady i Zadania

Sama znajomość wzorów to za mało. Trzeba umieć je zastosować w praktyce. Oto kilka przykładów:

Przykład 1: Oblicz pole trójkąta o podstawie 8 cm i wysokości opuszczonej na tę podstawę 5 cm.

Rozwiązanie:

P = (a * h) / 2 = (8 cm * 5 cm) / 2 = 40 cm² / 2 = 20 cm²

Przykład 2: Oblicz pole kwadratu o boku długości 6 cm.

Rozwiązanie:

P = a² = (6 cm)² = 36 cm²

Przykład 3: Oblicz pole prostokąta o bokach długości 4 cm i 7 cm.

Rozwiązanie:

P = a * b = 4 cm * 7 cm = 28 cm²

Przykład 4: Oblicz pole równoległoboku o podstawie 10 cm i wysokości opuszczonej na tę podstawę 3 cm.

Rozwiązanie:

P = a * h = 10 cm * 3 cm = 30 cm²

Przykład 5: Oblicz pole rombu o przekątnych długości 6 cm i 8 cm.

Rozwiązanie:

P = (d₁ * d₂) / 2 = (6 cm * 8 cm) / 2 = 48 cm² / 2 = 24 cm²

Przykład 6: Oblicz pole trapezu o podstawach długości 5 cm i 9 cm oraz wysokości 4 cm.

Rozwiązanie:

P = ((a + b) * h) / 2 = ((5 cm + 9 cm) * 4 cm) / 2 = (14 cm * 4 cm) / 2 = 56 cm² / 2 = 28 cm²

Wskazówka: Zawsze rysuj sobie rysunek pomocniczy. To ułatwia zrozumienie zadania i prawidłowe zastosowanie wzoru.

Zadania Złożone i Nietypowe

Na sprawdzianie mogą pojawić się również zadania bardziej złożone, wymagające logicznego myślenia i łączenia różnych wzorów. Na przykład, zadanie może polegać na obliczeniu pola figury, która jest złożona z kilku mniejszych wielokątów. W takim przypadku należy rozłożyć figurę na prostsze elementy, obliczyć pole każdego z nich, a następnie dodać pola do siebie.

Inny typ zadania to zadanie, w którym trzeba obliczyć wysokość lub długość boku, mając dane pole i inne wymiary. W takim przypadku należy przekształcić odpowiedni wzór, aby wyliczyć szukaną wielkość.

Przykład: Pole prostokąta wynosi 48 cm². Długość jednego z boków wynosi 8 cm. Oblicz długość drugiego boku.

Rozwiązanie:

P = a * b

48 cm² = 8 cm * b

b = 48 cm² / 8 cm = 6 cm

Długość drugiego boku wynosi 6 cm.

Real-World Examples

Pola wielokątów mają szerokie zastosowanie w życiu codziennym. Oto kilka przykładów:

Architektura: Obliczanie powierzchni podłóg, ścian i dachów podczas projektowania budynków.
Budownictwo: Obliczanie ilości materiałów potrzebnych do pokrycia powierzchni, np. płytek, farby, tapety.
Rolnictwo: Obliczanie powierzchni pól uprawnych, co jest niezbędne do planowania zasiewów i zbiorów.
Geodezja: Obliczanie powierzchni działek i terenów.
Krawiectwo: Obliczanie ilości materiału potrzebnego do uszycia ubrania.

Wyobraź sobie, że chcesz pomalować ścianę w swoim pokoju. Musisz obliczyć jej powierzchnię, aby wiedzieć, ile farby kupić. Powierzchnia ściany to po prostu pole prostokąta! Albo, jeśli chcesz kupić dywan do salonu, musisz znać wymiary podłogi (czyli pole prostokąta), aby wybrać odpowiedni rozmiar dywanu.

Wskazówki na Sprawdzian

Oto kilka praktycznych wskazówek, które pomogą Ci dobrze napisać sprawdzian:

Powtórz wzory: Upewnij się, że znasz wszystkie wzory na pola wielokątów na pamięć.
Rozwiązuj zadania: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz, jak stosować wzory w praktyce.
Rysuj rysunki: Zawsze rysuj sobie rysunek pomocniczy. To ułatwia zrozumienie zadania.
Sprawdzaj jednostki: Pamiętaj o podawaniu jednostek w wynikach (np. cm², m²).
Uważnie czytaj treść zadania: Zwróć uwagę na to, co jest dane, a co trzeba obliczyć.
Sprawdzaj wyniki: Po rozwiązaniu zadania sprawdź, czy wynik jest logiczny i sensowny.

Podsumowanie i Wezwanie do Działania

Przygotowanie do sprawdzianu z pól wielokątów wymaga systematycznej pracy i dobrego zrozumienia podstawowych pojęć i wzorów. Pamiętaj, że geometria jest wszędzie wokół nas, więc umiejętność obliczania pól jest bardzo przydatna w życiu codziennym. Nie poddawaj się! Poświęć czas na naukę, rozwiązuj zadania, a na pewno poradzisz sobie doskonale na sprawdzianie.

Teraz, gdy przeczytałeś ten artykuł, weź kartkę i długopis, i zacznij rozwiązywać zadania! Im więcej ćwiczysz, tym lepiej zrozumiesz materiał i tym pewniej będziesz czuł się na sprawdzianie. Powodzenia!