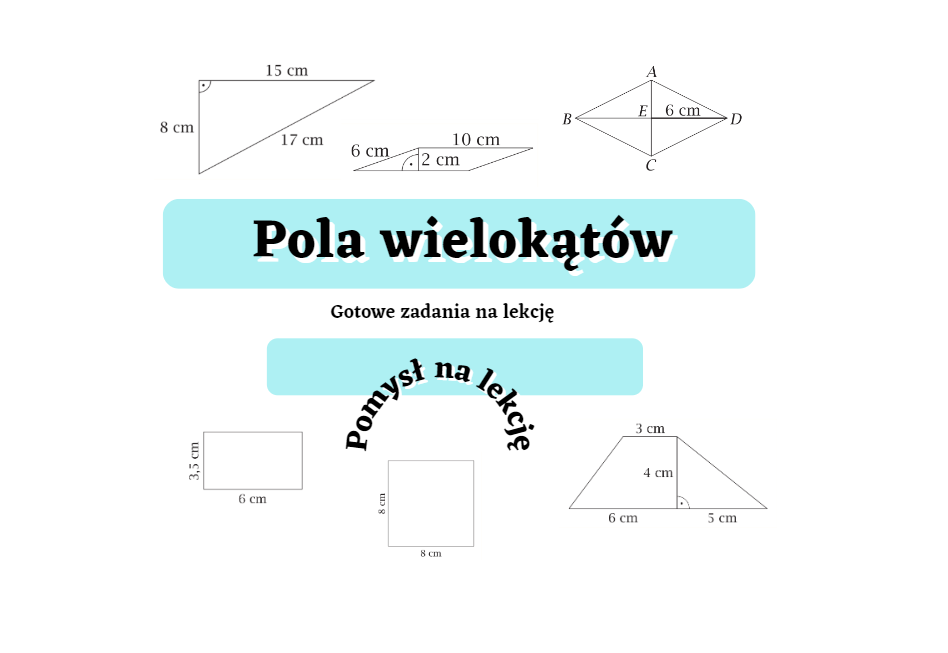
Pola Wielokątów Klasa 6 Sprawdzian

Rozumiem, że przygotowania do sprawdzianu z pól wielokątów w klasie 6 mogą być stresujące. Wiem, że geometria potrafi sprawiać trudności, szczególnie gdy zaczynamy zagłębiać się w obliczenia i wzory. Ten artykuł ma za zadanie pomóc Ci lepiej zrozumieć ten temat i poczuć się pewniej przed sprawdzianem. Pokażę Ci, jak ta wiedza przydaje się w codziennym życiu i postaram się wytłumaczyć trudne zagadnienia w prosty i przystępny sposób.

Dlaczego Pola Wielokątów Są Ważne?

Pomyśl o tym: malujesz pokój. Musisz obliczyć, ile farby potrzebujesz. Jak to zrobisz? Obliczając powierzchnię ścian, czyli de facto pola prostokątów i kwadratów! Albo, chcesz kupić nowy dywan do salonu. Potrzebujesz wiedzieć, jak duży dywan się zmieści. To znowu – pole! Wiedza o obliczaniu pól wielokątów nie jest tylko suchą teorią, ale praktyczną umiejętnością, która przydaje się w wielu sytuacjach. Budownictwo, architektura, projektowanie wnętrz, ogrodnictwo – wszędzie tam wykorzystuje się obliczanie pól powierzchni.

Realne Przykłady:

Remont pokoju: Obliczanie powierzchni ścian do malowania, układanie paneli podłogowych.
Urządzanie ogrodu: Planowanie rabat kwiatowych, układanie kostki brukowej.
Gotowanie: Obliczanie powierzchni blaszki do pieczenia ciasta.
Krawiectwo: Wycinanie materiału na ubrania.

Wbrew pozorom, geometria nie jest tylko abstrakcyjną nauką. Jest narzędziem, które pomaga nam zrozumieć i kształtować otaczający nas świat.

Co Musisz Wiedzieć do Sprawdzianu?

Sprawdzian z pól wielokątów w klasie 6 najczęściej obejmuje następujące zagadnienia:

Podstawowe wielokąty: kwadrat, prostokąt, równoległobok, romb, trapez, trójkąt.
Wzory na pola tych figur.
Umiejętność obliczania pól na podstawie podanych danych.
Zamiana jednostek pola (np. cm² na m²).
Rozwiązywanie zadań tekstowych związanych z polami.

Wzory, Które Musisz Zapamiętać:

Kwadrat: Pole = a * a (a - długość boku)
Prostokąt: Pole = a * b (a - długość, b - szerokość)
Równoległobok: Pole = a * h (a - długość podstawy, h - wysokość opuszczona na tę podstawę)
Romb: Pole = a * h (a - długość boku, h - wysokość opuszczona na ten bok) lub Pole = (d1 * d2) / 2 (d1, d2 - długości przekątnych)
Trójkąt: Pole = (a * h) / 2 (a - długość podstawy, h - wysokość opuszczona na tę podstawę)
Trapez: Pole = ((a + b) * h) / 2 (a, b - długości podstaw, h - wysokość)

Pamiętaj, że zrozumienie wzoru jest ważniejsze niż tylko jego wyuczenie się na pamięć. Spróbuj sobie wyobrazić, dlaczego dany wzór działa. Na przykład, pole trójkąta to połowa pola prostokąta o tych samych wymiarach. To ułatwi Ci zapamiętanie i stosowanie wzorów.

Jak Się Uczyć Efektywnie?

Nauka do sprawdzianu to nie tylko siedzenie nad książką. Oto kilka skutecznych metod, które pomogą Ci opanować materiał:

Rób zadania: To najważniejsze! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz wzory i sposoby ich stosowania. Zacznij od łatwiejszych zadań, a potem przejdź do trudniejszych.
Korzystaj z zasobów online: Istnieje wiele stron internetowych i filmów na YouTube, które tłumaczą geometrię w przystępny sposób. Znajdź te, które najbardziej Ci odpowiadają.
Ucz się z kimś: Wspólna nauka z kolegą lub koleżanką może być bardzo pomocna. Możecie sobie nawzajem tłumaczyć trudne zagadnienia i rozwiązywać zadania razem.
Rób krótkie przerwy: Nauka non-stop przez kilka godzin nie jest efektywna. Rób krótkie przerwy co 30-40 minut, aby Twój mózg mógł odpocząć i przetworzyć informacje.
Zastosuj to w praktyce: Spróbuj znaleźć przykłady obliczania pól w Twoim otoczeniu. Zmierz wymiary pokoju i oblicz jego powierzchnię. Zaprojektuj rabatę kwiatową i oblicz, ile ziemi potrzebujesz.

Typowe Błędy i Jak Ich Unikać

Nawet najlepsi uczniowie popełniają błędy. Ważne jest, aby wiedzieć, jakie błędy są najczęstsze i jak ich unikać:

Pomylenie wzorów: Upewnij się, że znasz wzory na pamięć i wiesz, kiedy który wzór zastosować. Napisz sobie kartkę ze wzorami i miej ją pod ręką podczas rozwiązywania zadań.
Błędne jednostki: Zawsze zwracaj uwagę na jednostki! Jeśli masz podane wymiary w centymetrach, a pole chcesz wyrazić w metrach kwadratowych, musisz najpierw zamienić jednostki. Pamiętaj, że 1 m = 100 cm, więc 1 m² = 10000 cm².
Błędne podstawianie danych do wzoru: Upewnij się, że podstawiasz właściwe wartości do wzoru. Na przykład, przy obliczaniu pola trójkąta musisz wziąć pod uwagę wysokość opuszczoną na daną podstawę, a nie długość innego boku.
Zapominanie o podzieleniu przez 2 (w przypadku trójkąta i rombu): To bardzo częsty błąd! Pamiętaj, że pole trójkąta to połowa pola prostokąta o tych samych wymiarach. Podobnie, w rombie (gdy korzystamy z przekątnych).
Brak dokładności obliczeń: Staraj się być dokładny w obliczeniach. Jeśli używasz kalkulatora, sprawdź, czy dobrze wpisałeś liczby. Jeśli obliczasz ręcznie, rób to starannie.

Adresowanie Kontrargumentów

Możesz pomyśleć: "Po co mi to wszystko? Nigdy nie będę malował pokoju ani projektował ogrodu!" To naturalne pytanie. Być może Twoja przyszłość nie będzie związana bezpośrednio z budownictwem czy architekturą. Jednak umiejętność logicznego myślenia, rozwiązywania problemów i analizowania danych, którą rozwijasz ucząc się geometrii, jest cenna w każdej dziedzinie. Nawet jeśli nie będziesz obliczał pól, będziesz umiał efektywniej podejmować decyzje, analizować sytuacje i znajdować rozwiązania. Geometria uczy Cię myśleć!

Inni mogą uważać, że nauka wzorów na pamięć jest bez sensu, ponieważ w dzisiejszych czasach wszystko można znaleźć w Internecie. Owszem, dostęp do informacji jest łatwy, ale rozumienie wzorów i umiejętność ich zastosowania jest kluczowa. Bez tego nie będziesz w stanie skutecznie korzystać z narzędzi online ani interpretować wyników.

Przykładowe Zadania i Rozwiązania

Oto kilka przykładowych zadań, które mogą pojawić się na sprawdzianie:

Zadanie 1: Oblicz pole prostokąta o długości 8 cm i szerokości 5 cm.
Rozwiązanie: Pole = a * b = 8 cm * 5 cm = 40 cm²
Zadanie 2: Oblicz pole trójkąta o podstawie 10 cm i wysokości 6 cm.
Rozwiązanie: Pole = (a * h) / 2 = (10 cm * 6 cm) / 2 = 30 cm²
Zadanie 3: Pokój ma wymiary 4 m x 5 m. Ile paneli podłogowych potrzeba do pokrycia podłogi, jeśli jeden panel ma wymiary 20 cm x 100 cm?
Rozwiązanie:
- Pole pokoju: 4 m * 5 m = 20 m²
- Pole jednego panelu: 20 cm * 100 cm = 2000 cm² = 0.2 m²
- Liczba paneli: 20 m² / 0.2 m² = 100 paneli

Podsumowanie i Co Dalej?

Przygotowanie do sprawdzianu z pól wielokątów wymaga systematycznej pracy i zrozumienia podstawowych wzorów. Pamiętaj, że geometria to nie tylko sucha teoria, ale praktyczna umiejętność, która przydaje się w życiu codziennym. Wykorzystaj podane wskazówki, rób zadania i nie bój się pytać, jeśli czegoś nie rozumiesz. Powodzenia na sprawdzianie!

Teraz, kiedy przeczytałeś ten artykuł, zastanów się: Jakie konkretne działania podejmiesz dzisiaj, aby lepiej przygotować się do sprawdzianu? Czy rozwiążesz kilka dodatkowych zadań? Porozmawiasz z nauczycielem o trudnych zagadnieniach? A może zorganizujesz sesję nauki z kolegą lub koleżanką? Wybór należy do Ciebie!