Pola Powierzchni I Objętości Graniastosłupów

Cześć! Witaj w naszym przewodniku, który pomoże Ci przygotować się do egzaminu z pola powierzchni i objętości graniastosłupów. Nie martw się, to nie jest tak trudne, jak się wydaje! Razem przejdziemy przez wszystkie najważniejsze zagadnienia, krok po kroku. Pamiętaj, regularna praktyka i zrozumienie podstawowych pojęć to klucz do sukcesu. Zaczynajmy!

Co to jest Graniastosłup?

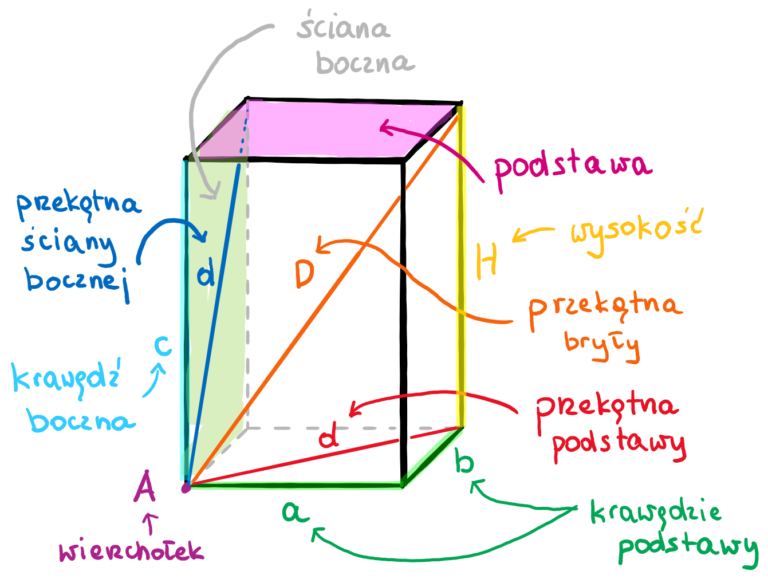
Na początek, ustalmy, czym w ogóle jest graniastosłup. Wyobraź sobie, że masz jakiś wielokąt (np. trójkąt, kwadrat, pięciokąt). Teraz wyciągnij ten wielokąt w górę, tworząc bryłę, której podstawą i górną ścianą jest ten sam wielokąt, a ściany boczne są prostokątami (lub równoległobokami, jeśli graniastosłup jest pochyły). To właśnie jest graniastosłup!

Definicja: Graniastosłup to bryła geometryczna, która ma dwie równoległe i przystające podstawy (wielokąty) oraz ściany boczne, które są prostokątami lub równoległobokami łączącymi odpowiadające boki podstaw.

Rodzaje Graniastosłupów

Graniastosłupy dzielimy na kilka rodzajów, w zależności od kształtu podstawy i ułożenia ścian bocznych:

• Graniastosłup prosty: Jego ściany boczne są prostokątami i są prostopadłe do podstawy.
• Graniastosłup pochyły: Jego ściany boczne są równoległobokami i nie są prostopadłe do podstawy.
• Graniastosłup prawidłowy: Jest to graniastosłup prosty, którego podstawa jest wielokątem foremnym (np. trójkąt równoboczny, kwadrat, pięciokąt foremny).

Pole Powierzchni Graniastosłupa

Pole powierzchni graniastosłupa to suma pól wszystkich jego ścian. Aby je obliczyć, musimy znać pole podstawy i pole powierzchni bocznej.

Wzór na Pole Powierzchni Całkowitej (Pc)

Pc = 2Pp + Pb

Gdzie:

• Pc to pole powierzchni całkowitej
• Pp to pole powierzchni podstawy
• Pb to pole powierzchni bocznej

Jak Obliczyć Pole Podstawy (Pp)?

To zależy od tego, jaki wielokąt znajduje się w podstawie. Musisz zastosować odpowiedni wzór na pole tego wielokąta:

• Trójkąt: Pp = (a * h) / 2 (gdzie a to długość podstawy trójkąta, a h to wysokość)
• Kwadrat: Pp = a² (gdzie a to długość boku kwadratu)
• Prostokąt: Pp = a * b (gdzie a i b to długości boków prostokąta)
• Pięciokąt foremny: Pp = (5 * a² * cot(π/5)) / 4 (gdzie a to długość boku pięciokąta) – ten wzór jest bardziej skomplikowany, ale warto go znać!
• Inne wielokąty: Możesz podzielić wielokąt na mniejsze, prostsze figury (np. trójkąty, prostokąty) i obliczyć pole każdej z nich osobno, a następnie zsumować.

Jak Obliczyć Pole Powierzchni Bocznej (Pb)?

Pole powierzchni bocznej to suma pól wszystkich ścian bocznych. W graniastosłupie prostym ściany boczne są prostokątami. W graniastosłupie pochyłym są to równoległoboki.

W graniastosłupie prostym: Pb = Obwód podstawy * Wysokość graniastosłupa

Pb = O * H (gdzie O to obwód podstawy, a H to wysokość graniastosłupa)

W graniastosłupie pochyłym: Musisz obliczyć pole każdego równoległoboku oddzielnie i je zsumować. Potrzebujesz znać długość boku równoległoboku i wysokość opuszczoną na ten bok.

Objętość Graniastosłupa

Objętość graniastosłupa to ilość miejsca, jaką zajmuje w przestrzeni. Na szczęście wzór na objętość jest stosunkowo prosty!

Wzór na Objętość (V)

V = Pp * H

Gdzie:

• V to objętość
• Pp to pole powierzchni podstawy (tak jak wcześniej!)
• H to wysokość graniastosłupa (odległość między podstawami)

Pamiętaj: Ten wzór działa zarówno dla graniastosłupów prostych, jak i pochyłych! Kluczem jest poprawne obliczenie pola podstawy.

Przykłady Obliczeniowe

Aby lepiej zrozumieć, jak to wszystko działa w praktyce, przeanalizujmy kilka przykładów:

Przykład 1: Graniastosłup prosty o podstawie trójkąta równobocznego

Załóżmy, że mamy graniastosłup prosty, którego podstawą jest trójkąt równoboczny o boku a = 5 cm. Wysokość graniastosłupa wynosi H = 10 cm. Oblicz pole powierzchni całkowitej i objętość.

1. Pole podstawy (Pp): Pp = (a² * √3) / 4 = (5² * √3) / 4 = (25 * √3) / 4 ≈ 10.83 cm²
2. Obwód podstawy (O): O = 3 * a = 3 * 5 = 15 cm
3. Pole powierzchni bocznej (Pb): Pb = O * H = 15 * 10 = 150 cm²
4. Pole powierzchni całkowitej (Pc): Pc = 2 * Pp + Pb = 2 * 10.83 + 150 = 171.66 cm²
5. Objętość (V): V = Pp * H = 10.83 * 10 = 108.3 cm³

Przykład 2: Graniastosłup prosty o podstawie kwadratu

Mamy graniastosłup prosty o podstawie kwadratu o boku a = 4 cm. Wysokość graniastosłupa wynosi H = 8 cm. Oblicz pole powierzchni całkowitej i objętość.

1. Pole podstawy (Pp): Pp = a² = 4² = 16 cm²
2. Obwód podstawy (O): O = 4 * a = 4 * 4 = 16 cm
3. Pole powierzchni bocznej (Pb): Pb = O * H = 16 * 8 = 128 cm²
4. Pole powierzchni całkowitej (Pc): Pc = 2 * Pp + Pb = 2 * 16 + 128 = 160 cm²
5. Objętość (V): V = Pp * H = 16 * 8 = 128 cm³

Wskazówki i Triki

• Rysuj! Zawsze narysuj sobie graniastosłup, żeby lepiej go zobaczyć i zrozumieć, jakie dane masz podane.
• Zapisuj wzory: Miej pod ręką listę wzorów na pola podstawowych figur geometrycznych.
• Sprawdzaj jednostki: Upewnij się, że wszystkie wymiary są w tych samych jednostkach (np. cm, m). Jeśli nie, zamień je!
• Ćwicz! Rozwiąż jak najwięcej zadań, żeby nabrać wprawy.

Podsumowanie

Gratulacje! Przeszliśmy przez wszystkie najważniejsze zagadnienia dotyczące pola powierzchni i objętości graniastosłupów. Pamiętaj o najważniejszych punktach:

• Graniastosłup to bryła o dwóch równoległych i przystających podstawach i ścianach bocznych w kształcie prostokątów lub równoległoboków.
• Pole powierzchni całkowitej: Pc = 2Pp + Pb
• Objętość: V = Pp * H
• Kluczem jest poprawne obliczenie pola podstawy!

Powodzenia na egzaminie! Pamiętaj, że z odpowiednim przygotowaniem na pewno dasz radę. Jeśli masz jakieś pytania, nie wahaj się ich zadać. Jesteśmy tu, żeby Ci pomóc!