Pola Powierzchni I Objętości Brył

Czy kiedykolwiek zastanawiałeś się, jak obliczyć, ile farby potrzebujesz do pomalowania pokoju? A może, jak dużo piasku zmieści się w piaskownicy Twojego dziecka? Te pytania, choć wydają się proste, prowadzą nas do fascynującego świata geometrii przestrzennej i obliczania pól powierzchni i objętości brył. Choć może wydawać się to abstrakcyjne, umiejętność ta jest niezwykle przydatna w życiu codziennym i w wielu zawodach.

Spróbujmy przez chwilę poczuć dyskomfort osoby, która ma za zadanie zaprojektować pudełko na prezent o nietypowym kształcie. Ile kartonu będzie potrzebne? Jak duży ma być prezent, aby się zmieścił? Bez znajomości geometrii przestrzennej i umiejętności obliczania powierzchni i objętości, zadanie to byłoby niezwykle trudne, a wręcz niemożliwe. Dlatego właśnie geometria przestrzenna ma tak ogromne znaczenie.

Pola Powierzchni i Objętości – Dlaczego są Tak Ważne?

Pola powierzchni i objętości brył nie są jedynie abstrakcyjnymi pojęciami z podręczników. Mają one realny wpływ na wiele aspektów naszego życia:

Budownictwo i Architektura: Obliczanie ilości materiałów budowlanych, takich jak cegły, beton czy farba, jest niemożliwe bez znajomości pól powierzchni i objętości. Architekci muszą precyzyjnie obliczać objętość pomieszczeń, aby zapewnić odpowiednią wentylację i oświetlenie.
Inżynieria: Inżynierowie wykorzystują te obliczenia do projektowania mostów, budynków, maszyn i urządzeń. Muszą oni uwzględniać wytrzymałość materiałów, ich objętość i powierzchnię, aby zapewnić bezpieczeństwo i funkcjonalność konstrukcji.
Opakowania: Projektanci opakowań muszą optymalizować objętość i powierzchnię pudełek i pojemników, aby zminimalizować koszty transportu i magazynowania.
Gotowanie i Pieczenie: Przepisy często podają objętości składników, a zrozumienie relacji między objętością a powierzchnią ciasta może pomóc w uzyskaniu idealnego wypieku.
Medycyna: Objętość organów może być wskaźnikiem zdrowia, a powierzchnia ciała jest wykorzystywana do obliczania dawek leków.

Można argumentować, że obecnie programy komputerowe i kalkulatory wykonują większość tych obliczeń automatycznie. To prawda, ale zrozumienie podstawowych zasad geometrii przestrzennej jest niezbędne, aby móc interpretować wyniki i weryfikować ich poprawność. Poleganie wyłącznie na narzędziach bez zrozumienia podstaw prowadzi do błędów i potencjalnych problemów.

Podstawowe Bryły i ich Wzory

Przyjrzyjmy się teraz kilku podstawowym bryłom i wzorom na obliczanie ich pól powierzchni i objętości:

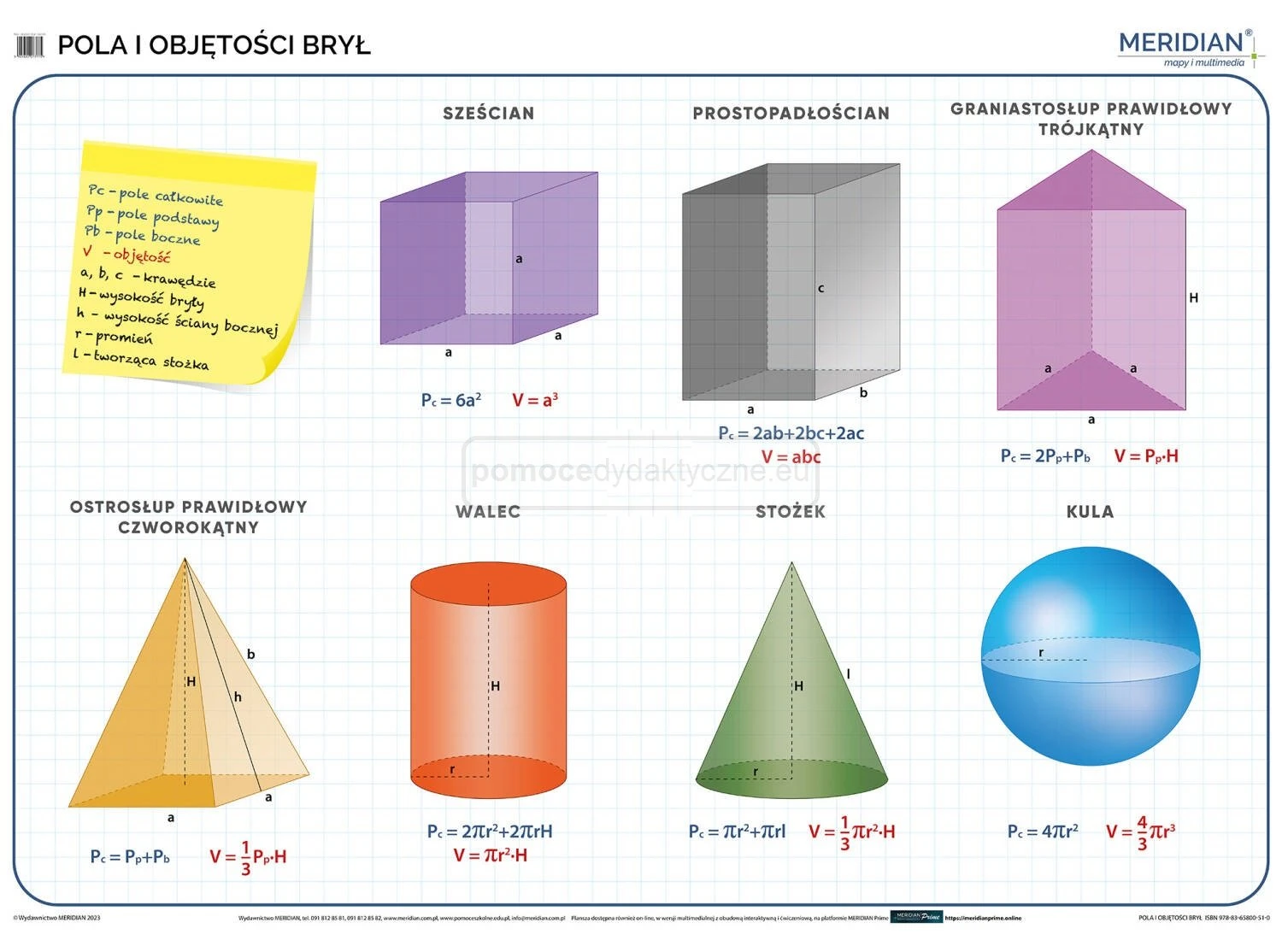
Sześcian

Sześcian to bryła, która ma sześć identycznych kwadratowych ścian. Jest to jedna z najprostszych brył do zrozumienia.

Pole powierzchni (Pc): Pc = 6 * a², gdzie 'a' to długość krawędzi sześcianu.
Objętość (V): V = a³, gdzie 'a' to długość krawędzi sześcianu.

Wyobraź sobie pudełko w kształcie sześcianu o krawędzi 5 cm. Jego pole powierzchni wynosiłoby 6 * 5² = 150 cm², a objętość 5³ = 125 cm³.

Prostopadłościan

Prostopadłościan to bryła, która ma sześć ścian w kształcie prostokątów. Sześcian jest szczególnym przypadkiem prostopadłościanu, gdzie wszystkie ściany są kwadratami.

Pole powierzchni (Pc): Pc = 2 * (ab + bc + ac), gdzie 'a', 'b' i 'c' to długości krawędzi prostopadłościanu.
Objętość (V): V = a * b * c, gdzie 'a', 'b' i 'c' to długości krawędzi prostopadłościanu.

Pomyśl o pudełku na buty, które ma wymiary 30 cm x 20 cm x 10 cm. Jego pole powierzchni wynosiłoby 2 * (30*20 + 20*10 + 30*10) = 2 * (600 + 200 + 300) = 2200 cm², a objętość 30 * 20 * 10 = 6000 cm³.

Walec

Walec to bryła, która ma dwie podstawy w kształcie kół i powierzchnię boczną w kształcie prostokąta, który jest zawinięty wokół tych kół.

Pole powierzchni (Pc): Pc = 2 * π * r² + 2 * π * r * h, gdzie 'r' to promień podstawy, a 'h' to wysokość walca.
Objętość (V): V = π * r² * h, gdzie 'r' to promień podstawy, a 'h' to wysokość walca.

Wyobraź sobie puszkę po napoju o promieniu 3 cm i wysokości 10 cm. Jej pole powierzchni wynosiłoby 2 * π * 3² + 2 * π * 3 * 10 ≈ 245 cm², a objętość π * 3² * 10 ≈ 283 cm³.

Stożek

Stożek to bryła, która ma podstawę w kształcie koła i powierzchnię boczną, która zwęża się do jednego punktu (wierzchołka).

Pole powierzchni (Pc): Pc = π * r² + π * r * l, gdzie 'r' to promień podstawy, a 'l' to długość tworzącej stożka.
Objętość (V): V = (1/3) * π * r² * h, gdzie 'r' to promień podstawy, a 'h' to wysokość stożka.

Pomyśl o rożku do lodów o promieniu 4 cm i wysokości 12 cm. Aby obliczyć pole powierzchni, musimy najpierw znaleźć długość tworzącej 'l'. Z twierdzenia Pitagorasa, l = √(r² + h²) = √(4² + 12²) ≈ 12.65 cm. Wtedy pole powierzchni wynosiłoby π * 4² + π * 4 * 12.65 ≈ 210 cm², a objętość (1/3) * π * 4² * 12 ≈ 201 cm³.

Kula

Kula to bryła, w której wszystkie punkty na jej powierzchni są w równej odległości od jednego punktu (środka).

Pole powierzchni (Pc): Pc = 4 * π * r², gdzie 'r' to promień kuli.
Objętość (V): V = (4/3) * π * r³, gdzie 'r' to promień kuli.

Wyobraź sobie piłkę o promieniu 7 cm. Jej pole powierzchni wynosiłoby 4 * π * 7² ≈ 616 cm², a objętość (4/3) * π * 7³ ≈ 1437 cm³.

Praktyczne Zastosowania Obliczeń

Zastanówmy się, jak te obliczenia można wykorzystać w praktyce. Na przykład, jeśli planujesz budowę basenu, musisz obliczyć jego objętość, aby wiedzieć, ile wody będzie potrzebne do jego napełnienia. Musisz także obliczyć pole powierzchni ścian basenu, aby określić ilość płytek ceramicznych potrzebnych do wykończenia.

Podobnie, jeśli pracujesz w branży logistycznej, musisz obliczać objętość różnych paczek i kontenerów, aby optymalizować ich transport. Znajomość pól powierzchni pozwala na obliczenie kosztów malowania konstrukcji stalowych, a także pozwala na oszacowanie strat ciepła w budynkach.

Rozwiązywanie Problemów – Krok po Kroku

Kiedy masz do czynienia z problemem związanym z polem powierzchni lub objętością, warto postępować zgodnie z następującymi krokami:

Zrozum Problem: Przeczytaj uważnie zadanie i upewnij się, że rozumiesz, o co jesteś pytany. Zidentyfikuj wszystkie dane, które są podane, i te, które musisz znaleźć.
Wybierz Odpowiedni Wzór: Zidentyfikuj bryłę, z którą masz do czynienia, i wybierz odpowiedni wzór na obliczenie jej pola powierzchni lub objętości.
Podstaw Dane do Wzoru: Podstaw wartości danych do wybranego wzoru. Upewnij się, że używasz odpowiednich jednostek miary.
Wykonaj Obliczenia: Wykonaj obliczenia zgodnie z kolejnością działań. Użyj kalkulatora, jeśli to konieczne.
Sprawdź Wynik: Sprawdź, czy wynik jest sensowny w kontekście zadania. Czy jednostki miary są poprawne? Czy wynik jest realistyczny?

Wykorzystanie Technologii

Współcześnie mamy dostęp do wielu narzędzi, które ułatwiają obliczanie pól powierzchni i objętości. Kalkulatory naukowe, programy do projektowania 3D i aplikacje mobilne mogą wykonywać te obliczenia szybko i dokładnie. Jednak, jak już wcześniej wspomniano, ważne jest, aby rozumieć podstawowe zasady geometrii przestrzennej, aby móc weryfikować wyniki i interpretować je w odpowiedni sposób.

Istnieją również platformy edukacyjne online oferujące interaktywne kursy i ćwiczenia z geometrii przestrzennej. Mogą one być bardzo pomocne w utrwalaniu wiedzy i rozwijaniu umiejętności rozwiązywania problemów.

Podsumowanie

Obliczanie pól powierzchni i objętości brył to umiejętność, która ma szerokie zastosowanie w życiu codziennym i w wielu zawodach. Choć na początku może wydawać się trudna, z odpowiednim podejściem i regularną praktyką można ją opanować. Zrozumienie podstawowych zasad geometrii przestrzennej jest kluczowe do rozwiązywania problemów praktycznych i podejmowania świadomych decyzji.

Pamiętaj, że geometria przestrzenna to nie tylko zbiór wzorów, ale przede wszystkim sposób myślenia o świecie w trzech wymiarach. Rozwijanie tej umiejętności pozwala nam lepiej rozumieć otaczającą nas rzeczywistość i skuteczniej rozwiązywać problemy.

Czy zastanawiasz się, jak możesz wykorzystać wiedzę na temat pól powierzchni i objętości w swojej codziennej pracy lub w życiu prywatnym? Jakie projekty lub zadania mogłyby skorzystać z bardziej precyzyjnych obliczeń?