Pola Figur Zadania Klasa 5

Witaj w fascynującym świecie figur i zadań geometrycznych w klasie 5! Matematyka to nie tylko liczby, ale także kształty, wzory i logiczne myślenie. Ten artykuł pomoże Ci zrozumieć, jak analizować i rozwiązywać zadania dotyczące figur geometrycznych, które często pojawiają się na lekcjach matematyki i sprawdzianach. Przygotuj się na odkrywanie tajemnic prostokątów, kwadratów, trójkątów i wielu innych ciekawych kształtów!

Podstawowe figury geometryczne i ich własności

W klasie 5 poznajesz podstawowe figury geometryczne na płaszczyźnie. Zrozumienie ich właściwości jest kluczowe do rozwiązywania zadań.

Prostokąt i kwadrat

Prostokąt to czworokąt, który ma dwa boki o równej długości (długość i szerokość) i wszystkie kąty proste (90 stopni). Kwadrat to szczególny przypadek prostokąta, w którym wszystkie boki są równe. Umiejętność rozpoznawania prostokątów i kwadratów jest bardzo ważna. Pomyśl o ramce na zdjęcia - to często prostokąt. A plansza do gry w szachy? Zazwyczaj kwadrat.

Obwód prostokąta obliczamy, dodając długości wszystkich boków: Obwód = 2 * długość + 2 * szerokość. Dla kwadratu, gdzie wszystkie boki są równe, wzór upraszcza się do: Obwód = 4 * bok.

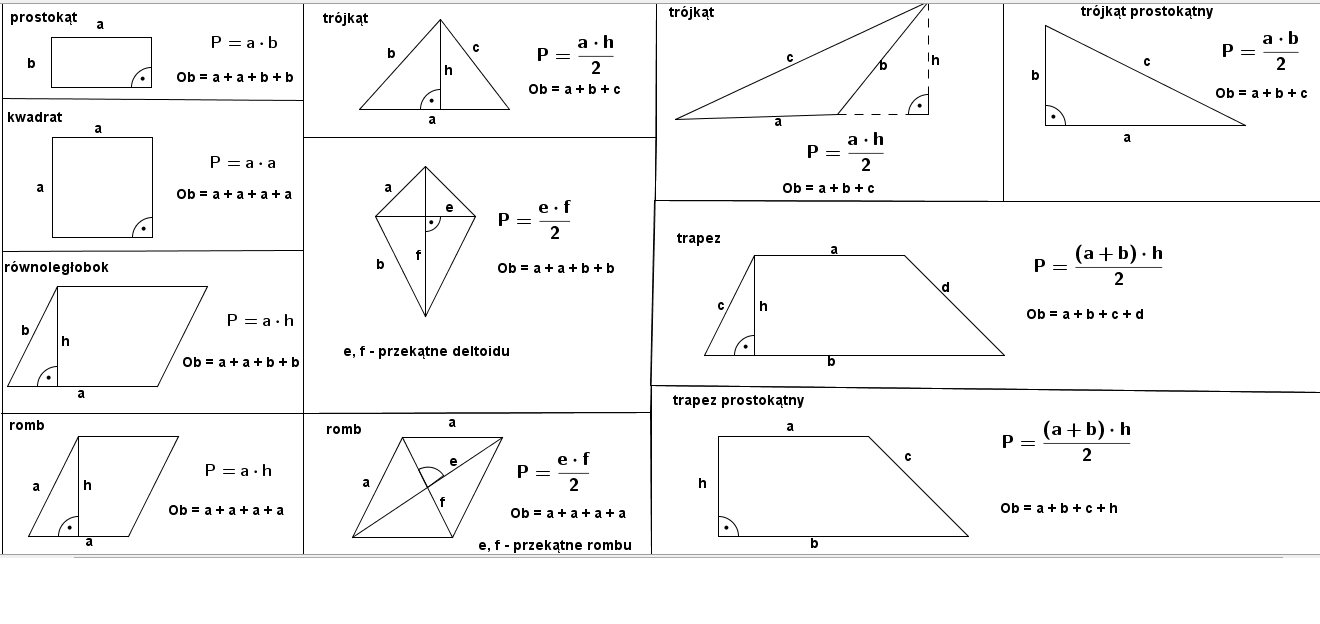
Pole prostokąta obliczamy, mnożąc długość przez szerokość: Pole = długość * szerokość. Dla kwadratu: Pole = bok * bok (często zapisywane jako bok²).

Przykład: Pokój ma kształt prostokąta o długości 5 metrów i szerokości 4 metry. Obwód pokoju wynosi 2 * 5 + 2 * 4 = 10 + 8 = 18 metrów. Pole pokoju wynosi 5 * 4 = 20 metrów kwadratowych.

Trójkąt

Trójkąt to figura geometryczna, która ma trzy boki i trzy kąty. Istnieje wiele rodzajów trójkątów: równoboczny (wszystkie boki równe), równoramienny (dwa boki równe), różnoboczny (wszystkie boki różne), prostokątny (jeden kąt prosty).

Obwód trójkąta obliczamy, dodając długości wszystkich jego boków: Obwód = bok1 + bok2 + bok3.

Pole trójkąta obliczamy, mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę, a następnie dzieląc wynik przez 2: Pole = (podstawa * wysokość) / 2. Wysokość to odcinek prostopadły do podstawy, łączący podstawę z wierzchołkiem naprzeciwko.

Przykład: Trójkąt ma podstawę o długości 6 cm i wysokość opuszczoną na tę podstawę o długości 4 cm. Pole trójkąta wynosi (6 * 4) / 2 = 24 / 2 = 12 cm kwadratowych.

Równoległobok i romb

Równoległobok to czworokąt, który ma dwie pary boków równoległych. Romb to równoległobok, który ma wszystkie boki równe.

Obwód równoległoboku obliczamy, dodając długości wszystkich boków: Obwód = 2 * bok1 + 2 * bok2. Dla rombu, gdzie wszystkie boki są równe, wzór upraszcza się do: Obwód = 4 * bok.

Pole równoległoboku obliczamy, mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę: Pole = podstawa * wysokość.

Pole rombu możemy obliczyć na dwa sposoby: tak jak pole równoległoboku (podstawa * wysokość) lub mnożąc długości przekątnych przez siebie, a następnie dzieląc wynik przez 2: Pole = (przekątna1 * przekątna2) / 2.

Trapez

Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych (zwanych podstawami trapezu).

Obwód trapezu obliczamy, dodając długości wszystkich jego boków: Obwód = podstawa1 + podstawa2 + bok3 + bok4.

Pole trapezu obliczamy, dodając długości obu podstaw, mnożąc wynik przez wysokość i dzieląc przez 2: Pole = ((podstawa1 + podstawa2) * wysokość) / 2. Wysokość trapezu to odcinek prostopadły do podstaw, łączący obie podstawy.

Koło i okrąg

Okrąg to zbiór wszystkich punktów na płaszczyźnie, które znajdują się w równej odległości od jednego punktu zwanego środkiem okręgu. Odległość od środka okręgu do dowolnego punktu na okręgu nazywamy promieniem (r). Odcinek łączący dwa punkty na okręgu i przechodzący przez środek okręgu nazywamy średnicą (d). Średnica jest dwa razy dłuższa od promienia: d = 2 * r.

Koło to obszar ograniczony okręgiem. Okrąg jest brzegiem koła, a koło to okrąg wraz z jego wnętrzem.

Obwód okręgu (długość okręgu) obliczamy ze wzoru: Obwód = 2 * π * r, gdzie π (pi) to liczba niewymierna w przybliżeniu równa 3,14.

Pole koła obliczamy ze wzoru: Pole = π * r².

Rozwiązywanie zadań z figur geometrycznych

Rozwiązywanie zadań z figur geometrycznych wymaga umiejętności czytania ze zrozumieniem, analizy danych i wyboru odpowiedniego wzoru. Oto kilka wskazówek, które mogą Ci pomóc:

Przeczytaj uważnie treść zadania: Zrozum, o co pytają i jakie dane są podane.
Narysuj rysunek pomocniczy: Rysunek często pomaga wizualizować problem i dostrzec zależności.
Wypisz dane: Zapisz wszystkie znane wartości i oznacz niewiadome.
Wybierz odpowiedni wzór: Zastanów się, który wzór pasuje do danej figury i pytania w zadaniu.
Podstaw dane do wzoru: Uważaj na jednostki! Upewnij się, że wszystkie dane są w tych samych jednostkach (np. metry, centymetry).
Oblicz wynik: Wykonaj obliczenia krok po kroku, sprawdzając poprawność każdego kroku.
Sprawdź odpowiedź: Czy odpowiedź ma sens? Czy wynik jest realistyczny w kontekście zadania?

Przykłady zadań i ich rozwiązania

Zadanie 1: Oblicz pole prostokąta, którego jeden bok ma długość 8 cm, a drugi jest o 3 cm dłuższy.

Rozwiązanie:

Dane: bok1 = 8 cm, bok2 = bok1 + 3 cm = 8 cm + 3 cm = 11 cm
Wzór: Pole prostokąta = bok1 * bok2
Obliczenia: Pole = 8 cm * 11 cm = 88 cm²
Odpowiedź: Pole prostokąta wynosi 88 cm².

Zadanie 2: Obwód kwadratu wynosi 24 cm. Oblicz długość boku tego kwadratu.

Rozwiązanie:

Dane: Obwód = 24 cm
Wzór: Obwód kwadratu = 4 * bok
Przekształcenie wzoru: bok = Obwód / 4
Obliczenia: bok = 24 cm / 4 = 6 cm
Odpowiedź: Długość boku kwadratu wynosi 6 cm.

Zadanie 3: Oblicz pole trójkąta prostokątnego, którego przyprostokątne mają długości 5 cm i 12 cm.

Rozwiązanie:

Dane: podstawa = 5 cm, wysokość = 12 cm (w trójkącie prostokątnym przyprostokątne są jednocześnie podstawą i wysokością)
Wzór: Pole trójkąta = (podstawa * wysokość) / 2
Obliczenia: Pole = (5 cm * 12 cm) / 2 = 60 cm² / 2 = 30 cm²
Odpowiedź: Pole trójkąta wynosi 30 cm².

Figury geometryczne w życiu codziennym

Figury geometryczne otaczają nas wszędzie. Prostokąty i kwadraty widzimy w budynkach, oknach, drzwiach, książkach. Trójkąty występują w konstrukcjach mostów, dachach domów, znakach drogowych. Koła widzimy w kołach samochodów, tarczach zegarów, talerzach. Zrozumienie geometrii pomaga nam lepiej rozumieć świat wokół nas.

Na przykład, jeśli chcemy kupić dywan do pokoju, musimy zmierzyć długość i szerokość pokoju, aby obliczyć pole powierzchni, które chcemy pokryć. Jeśli chcemy ogrodzić ogródek, musimy zmierzyć długość boków ogródka, aby obliczyć długość potrzebnego ogrodzenia.

Podsumowanie i dalsza nauka

Gratulacje! Zyskałeś solidną wiedzę na temat podstawowych figur geometrycznych i sposobów rozwiązywania zadań z nimi związanych. Pamiętaj, że praktyka czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zasady geometrii i tym pewniej będziesz czuć się na lekcjach matematyki.

Co możesz zrobić dalej?

Rozwiązuj zadania z podręcznika i ćwiczeń.
Szukaj dodatkowych zadań w Internecie.
Graj w gry edukacyjne związane z geometrią.
Obserwuj figury geometryczne w swoim otoczeniu i próbuj obliczać ich obwody i pola.
Zadawaj pytania nauczycielowi, jeśli czegoś nie rozumiesz.

Powodzenia w dalszej nauce matematyki! Pamiętaj, że matematyka może być fascynująca i przydatna. Odkrywaj jej piękno i wykorzystuj ją w swoim życiu!