Pola Figur Klasa 6 Sprawdzian

Sprawdzian z pól figur płaskich to kluczowy element edukacji matematycznej w 6 klasie szkoły podstawowej. To moment, w którym uczniowie weryfikują swoją wiedzę i umiejętności w zakresie obliczania powierzchni różnych kształtów. Celem tego artykułu jest omówienie najważniejszych zagadnień związanych z tym sprawdzianem, aby pomóc uczniom w jego skutecznym przygotowaniu.

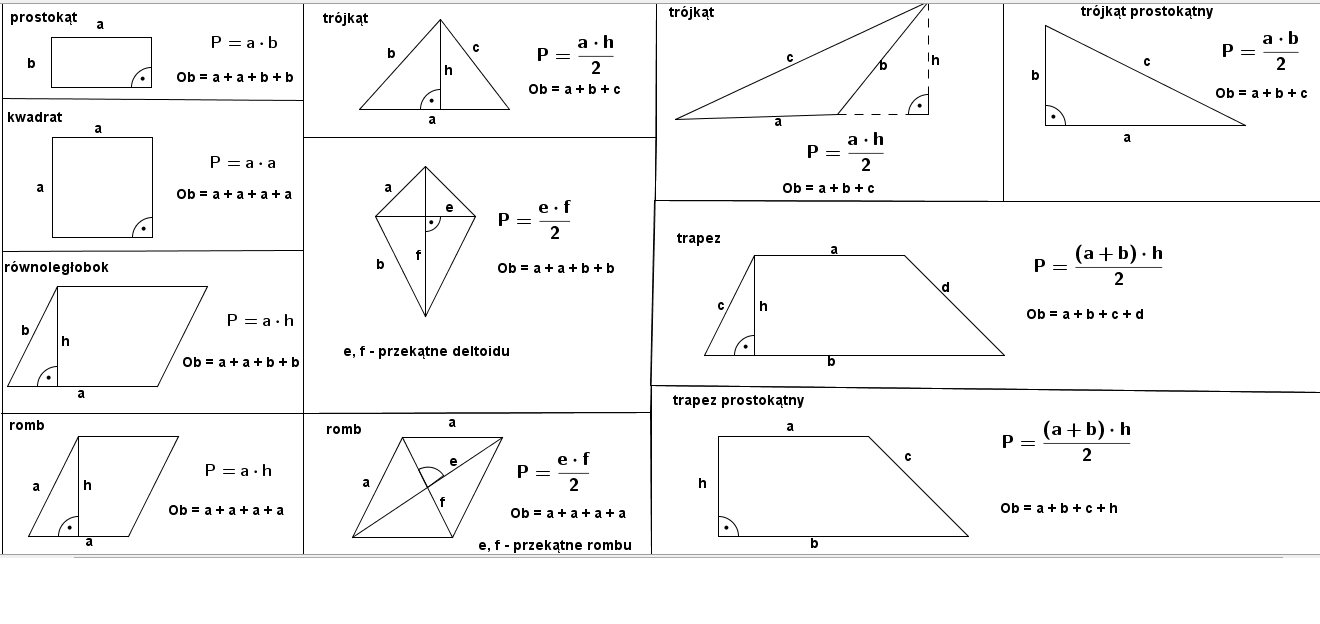
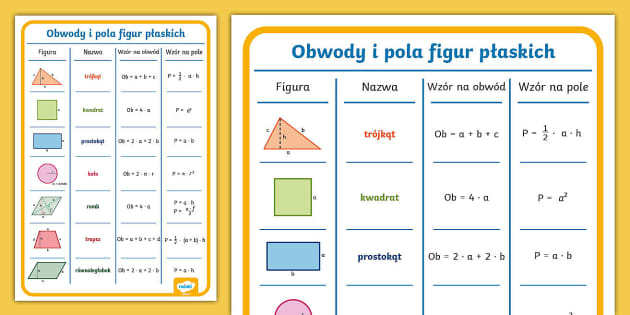
Podstawowe figury i ich pola

Podczas sprawdzianu z pewnością pojawią się zadania dotyczące obliczania pól podstawowych figur geometrycznych. Kluczowe jest dokładne zrozumienie wzorów i umiejętność ich zastosowania w praktyce.

Kwadrat i Prostokąt

Najprostsze figury, ale fundamentalne. Kwadrat to czworokąt o wszystkich bokach równych i wszystkich kątach prostych. Jego pole obliczamy, mnożąc długość boku przez siebie: P = a * a = a². Prostokąt z kolei ma przeciwległe boki równe i wszystkie kąty proste. Jego pole obliczamy, mnożąc długość jednego boku przez długość drugiego: P = a * b.

Przykład: Kwadrat o boku 5 cm ma pole 25 cm² (5cm * 5cm). Prostokąt o bokach 3 cm i 7 cm ma pole 21 cm² (3cm * 7cm).

Trójkąt

Obliczanie pola trójkąta jest nieco bardziej skomplikowane, ale nadal oparte na prostym wzorze. Pole trójkąta obliczamy, mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę, a następnie dzieląc wynik przez 2: P = (a * h) / 2. Ważne jest, aby pamiętać, że wysokość musi być prostopadła do podstawy.

Przykład: Trójkąt o podstawie 8 cm i wysokości 6 cm ma pole 24 cm² (8cm * 6cm / 2).

Równoległobok i Romb

Równoległobok to czworokąt, którego przeciwległe boki są równoległe. Jego pole obliczamy, mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę: P = a * h. Podobnie jak w przypadku trójkąta, wysokość musi być prostopadła do podstawy.

Romb to szczególny przypadek równoległoboku, w którym wszystkie boki są równe. Można obliczyć jego pole jak pole równoległoboku (P = a * h) lub za pomocą długości przekątnych: P = (e * f) / 2, gdzie e i f to długości przekątnych.

Przykład: Równoległobok o podstawie 10 cm i wysokości 4 cm ma pole 40 cm² (10cm * 4cm). Romb o przekątnych 6 cm i 8 cm ma pole 24 cm² (6cm * 8cm / 2).

Trapez

Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych (zwanych podstawami). Pole trapezu obliczamy, dodając długości podstaw, mnożąc wynik przez wysokość i dzieląc przez 2: P = ((a + b) * h) / 2, gdzie a i b to długości podstaw, a h to wysokość.

Przykład: Trapez o podstawach 5 cm i 7 cm oraz wysokości 3 cm ma pole 18 cm² ((5cm + 7cm) * 3cm / 2).

Zadania złożone i nietypowe sytuacje

Sprawdzian może zawierać zadania, w których trzeba połączyć wiedzę o różnych figurach. Może to oznaczać obliczanie pola figury, która składa się z kilku mniejszych figur, albo obliczanie pola figury "wyciętej" z innej.

Figury złożone

Aby obliczyć pole figury złożonej, należy rozłożyć ją na prostsze figury, takie jak kwadraty, prostokąty, trójkąty itp. Następnie obliczamy pole każdej z tych figur i sumujemy je. Kluczem jest uważne przeczytanie treści zadania i zidentyfikowanie wszystkich potrzebnych wymiarów.

Przykład: Figura składa się z prostokąta o wymiarach 4 cm x 6 cm i trójkąta o podstawie 4 cm i wysokości 3 cm, który jest do niego doklejony na krótszym boku. Pole prostokąta to 24 cm², a pole trójkąta to 6 cm². Całkowite pole figury to 30 cm².

Figury "wycięte"

W zadaniach tego typu mamy jedną figurę, z której wycięto inną. Aby obliczyć pole powstałej figury, należy obliczyć pole większej figury i odjąć od niego pole figury wyciętej.

Przykład: Z kwadratu o boku 8 cm wycięto koło o promieniu 2 cm. Pole kwadratu to 64 cm². Pole koła to π * 2² ≈ 12.56 cm². Pole figury po wycięciu koła to około 51.44 cm².

Jednostki pola i zamiana jednostek

Pamiętaj o jednostkach! Pole zawsze wyrażamy w jednostkach kwadratowych, np. cm², m², km². Ważna jest umiejętność zamiany jednostek pola. Na przykład: 1 m² = 10000 cm², 1 km² = 1000000 m². Upewnij się, że wszystkie wymiary w zadaniu są podane w tej samej jednostce przed rozpoczęciem obliczeń.

Przykład: Jeśli masz długość w metrach i szerokość w centymetrach, zamień jedną z tych wartości, aby obie były w tej samej jednostce (np. zamień metry na centymetry lub centymetry na metry).

Wskazówki i strategie na sprawdzian

Przeczytaj uważnie zadanie: Zwróć uwagę na wszystkie szczegóły i dane.
Zapisz wzory: Zanim zaczniesz obliczenia, zapisz wzór, który będziesz używać.
Upewnij się, że jednostki są spójne: Wszystkie wymiary powinny być w tej samej jednostce.
Sprawdź wynik: Po obliczeniu sprawdź, czy wynik jest sensowny i czy jednostka jest poprawna.
Rysuj rysunki: Jeśli to możliwe, narysuj rysunek figury, aby lepiej zrozumieć zadanie.

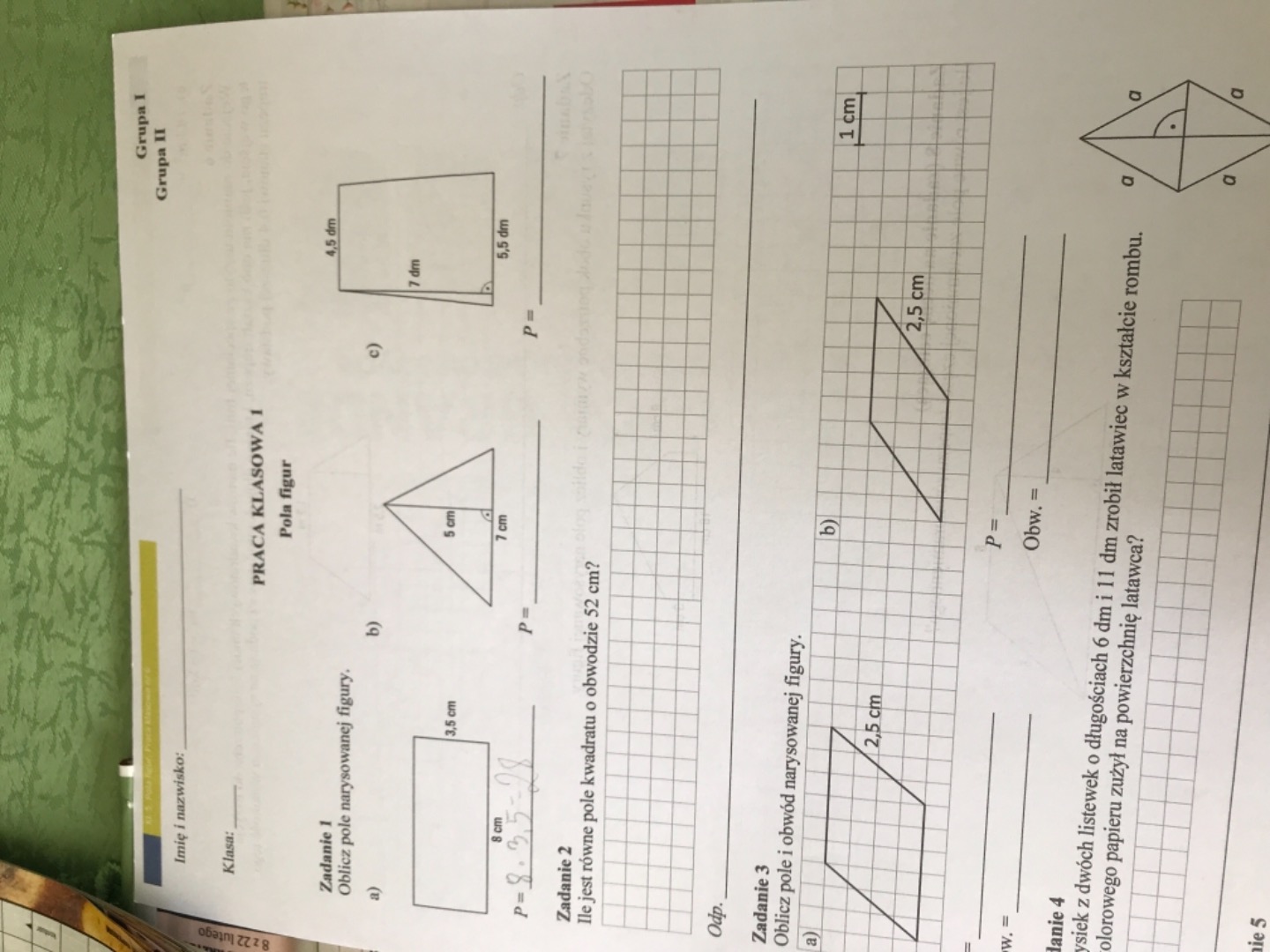
Przykładowe zadania i rozwiązania

Zadanie 1: Oblicz pole trapezu równoramiennego, którego podstawy mają długości 6 cm i 10 cm, a wysokość wynosi 4 cm.

Rozwiązanie: Używamy wzoru na pole trapezu: P = ((a + b) * h) / 2. Podstawiamy dane: P = ((6 cm + 10 cm) * 4 cm) / 2 = (16 cm * 4 cm) / 2 = 64 cm² / 2 = 32 cm². Odpowiedź: Pole trapezu wynosi 32 cm².

Zadanie 2: Oblicz pole rombu, którego przekątne mają długości 8 cm i 12 cm.

Rozwiązanie: Używamy wzoru na pole rombu z przekątnymi: P = (e * f) / 2. Podstawiamy dane: P = (8 cm * 12 cm) / 2 = 96 cm² / 2 = 48 cm². Odpowiedź: Pole rombu wynosi 48 cm².

Zadanie 3: Pokój ma kształt prostokąta o wymiarach 5 m x 4 m. Ile puszek farby potrzeba do pomalowania podłogi, jeśli jedna puszka wystarcza na pomalowanie 2 m²?

Rozwiązanie: Obliczamy pole prostokąta: P = a * b = 5 m * 4 m = 20 m². Następnie dzielimy pole pokoju przez powierzchnię, którą można pomalować jedną puszką: 20 m² / 2 m²/puszkę = 10 puszek. Odpowiedź: Potrzeba 10 puszek farby.

Znaczenie znajomości pól figur w życiu codziennym

Zrozumienie pól figur geometrycznych ma ogromne znaczenie w życiu codziennym, chociaż często nie zdajemy sobie z tego sprawy. Od planowania remontu mieszkania, przez obliczanie ilości materiałów potrzebnych do budowy, po projektowanie ogrodów i przestrzeni miejskich – wiedza ta jest niezbędna w wielu dziedzinach.

Przykłady: Architekci wykorzystują wiedzę o polach figur do projektowania budynków, tak aby efektywnie wykorzystać przestrzeń. Ogrodnicy obliczają pola powierzchni rabat, aby odpowiednio dobrać ilość roślin i nawozów. Malarze obliczają powierzchnię ścian, aby oszacować ilość potrzebnej farby. Projektanci wnętrz dobierają dywany i meble, uwzględniając pole powierzchni pomieszczeń.

Umiejętność obliczania pól figur to fundament dla dalszej nauki matematyki i fizyki. Bez tej wiedzy trudno jest zrozumieć bardziej zaawansowane zagadnienia, takie jak obliczanie objętości brył, analiza danych statystycznych czy rozwiązywanie problemów inżynieryjnych.

Sprawdzian z pól figur w 6 klasie to ważny krok w edukacji matematycznej. Dokładne przygotowanie, zrozumienie wzorów i umiejętność ich zastosowania w praktyce to klucz do sukcesu. Nie zapomnij o jednostkach i o sprawdzaniu wyników. Powodzenia na sprawdzianie!