Pola Figur Klasa 5 Zadania

Drodzy Rodzice i Uczniowie klasy 5! Zmagacie się z geometrii, a dokładniej z polami figur? Nie jesteście sami! Wiele osób w tym wieku ma trudności z zrozumieniem, jak obliczyć pole prostokąta, kwadratu, równoległoboku, rombu czy trójkąta. Ten artykuł powstał, aby pomóc Wam uporać się z tymi wyzwaniami i sprawić, że geometria stanie się bardziej zrozumiała i, co najważniejsze, przyjemna!

Dlaczego pola figur są ważne?

Zanim przejdziemy do wzorów i zadań, warto zastanowić się, dlaczego w ogóle musimy to umieć. To nie tylko abstrakcyjne ćwiczenia w podręczniku. Umiejętność obliczania pól figur przydaje się w wielu sytuacjach w prawdziwym życiu:

• Planowanie remontu: Ile farby potrzebujesz do pomalowania ściany? Ile płytek zmieści się na podłodze? Znając wymiary i pola powierzchni, możesz to łatwo obliczyć!
• Projektowanie ogrodu: Ile trawy musisz kupić, aby obsiać trawnik? Jaką powierzchnię zajmą rabaty kwiatowe?
• Gotowanie: Czasami przepisy podają proporcje składników w zależności od wielkości blachy do pieczenia.
• Praca zawodowa: Architekci, inżynierowie, projektanci - oni wszyscy na co dzień używają wiedzy o polach figur!

Widzicie? Geometria to nie tylko nauka dla nauki, ale praktyczna umiejętność, która ułatwia życie.

Podstawowe figury i ich pola

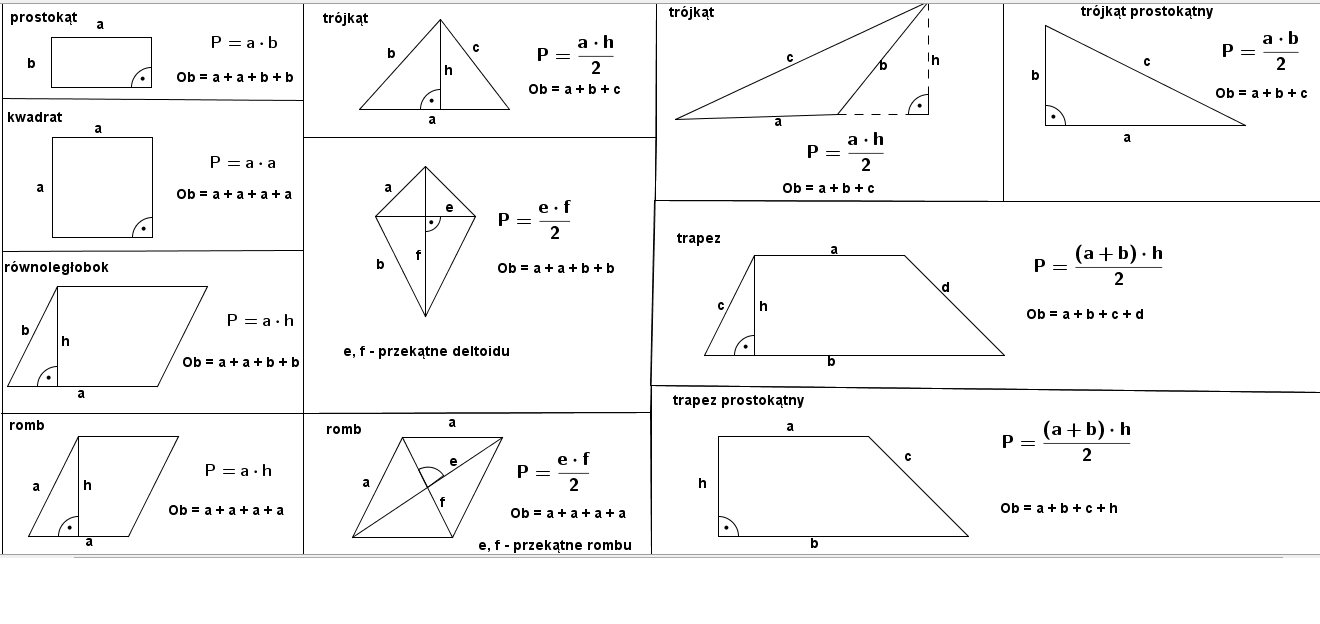
Zacznijmy od podstaw. Oto najważniejsze figury i wzory na obliczanie ich pól:

Prostokąt i Kwadrat

Prostokąt: To figura, która ma cztery kąty proste i przeciwległe boki równej długości. Jego pole obliczamy bardzo prosto: mnożymy długość jednego boku (a) przez długość drugiego boku (b). Wzór: P = a * b

Kwadrat: To szczególny przypadek prostokąta, w którym wszystkie boki są równe. Oznaczamy długość boku jako a. Wzór: P = a * a = a²

Przykład: Prostokąt ma boki długości 5 cm i 8 cm. Jego pole to 5 cm * 8 cm = 40 cm². Kwadrat ma bok długości 6 cm. Jego pole to 6 cm * 6 cm = 36 cm².

Równoległobok

Równoległobok: To czworokąt, który ma dwie pary boków równoległych. Jego pole obliczamy, mnożąc długość podstawy (a) przez wysokość (h) opuszczoną na tę podstawę. Ważne, aby pamiętać, że wysokość jest odcinkiem prostopadłym do podstawy.

Analogia: Wyobraź sobie, że równoległobok to "przechylony" prostokąt. Możesz odciąć trójkąt z jednej strony i przenieść go na drugą, tworząc prostokąt. Pole się nie zmieni, tylko figura inaczej wygląda.

Przykład: Równoległobok ma podstawę długości 10 cm, a wysokość opuszczona na tę podstawę wynosi 4 cm. Jego pole to 10 cm * 4 cm = 40 cm².

Romb

Romb: To równoległobok, który ma wszystkie boki równe. Możemy obliczyć jego pole tak samo jak pole równoległoboku (P = a * h), ale romb ma jeszcze jeden sposób na obliczenie pola: mnożymy długości jego przekątnych (e i f) i dzielimy przez 2.

Dlaczego tak? Romb można podzielić na cztery przystające trójkąty prostokątne. Każdy z nich ma pole równe (1/2) * (e/2) * (f/2). Zatem pole całego rombu to 4 * (1/2) * (e/2) * (f/2) = (e * f) / 2.

Przykład: Romb ma przekątne długości 8 cm i 6 cm. Jego pole to (8 cm * 6 cm) / 2 = 24 cm².

Trójkąt

Trójkąt: To figura o trzech bokach. Jego pole obliczamy, mnożąc długość podstawy (a) przez wysokość (h) opuszczoną na tę podstawę i dzieląc przez 2.

Wyjaśnienie: Można sobie wyobrazić, że trójkąt to "połowa" równoległoboku. Jeśli do trójkąta "dokleimy" drugi, identyczny trójkąt, otrzymamy równoległobok. Stąd wzór na pole trójkąta jest połową wzoru na pole równoległoboku.

Przykład: Trójkąt ma podstawę długości 7 cm, a wysokość opuszczona na tę podstawę wynosi 5 cm. Jego pole to (7 cm * 5 cm) / 2 = 17,5 cm².

Typowe błędy i jak ich unikać

Podczas obliczania pól figur uczniowie często popełniają te same błędy:

• Pomylenie wzorów: Upewnij się, że używasz właściwego wzoru dla danej figury. Wypisz sobie wszystkie wzory na kartce i miej je pod ręką.
• Używanie nieprawidłowych jednostek: Pamiętaj, że pole wyrażamy w jednostkach kwadratowych (cm², m², itp.).
• Źle zmierzona wysokość: Wysokość musi być prostopadła do podstawy. Nie myl jej z długością boku figury!
• Zapominanie o podzieleniu przez 2 w przypadku trójkąta: To bardzo częsty błąd!
• Nieczytanie uważnie zadania: Zawsze dokładnie przeczytaj treść zadania i upewnij się, że rozumiesz, o co pytają.

Przykładowe zadania z rozwiązaniami

Teraz czas na praktykę! Oto kilka przykładowych zadań z rozwiązaniami:

Zadanie 1:

Pokój ma kształt prostokąta o wymiarach 4 m x 5 m. Ile metrów kwadratowych parkietu potrzeba do wyłożenia podłogi?

Rozwiązanie: Używamy wzoru na pole prostokąta: P = a * b = 4 m * 5 m = 20 m². Odpowiedź: Potrzeba 20 m² parkietu.

Zadanie 2:

Trapez równoramienny ma podstawy długości 6 cm i 10 cm oraz wysokość 4 cm. Oblicz pole tego trapezu.

Rozwiązanie: Wzór na pole trapezu to P = ((a + b) * h) / 2, gdzie a i b to długości podstaw, a h to wysokość. Zatem P = ((6 cm + 10 cm) * 4 cm) / 2 = (16 cm * 4 cm) / 2 = 32 cm².

Zadanie 3:

Dywan ma kształt rombu o przekątnych długości 2 m i 3 m. Jakie jest pole tego dywanu?

Rozwiązanie: Używamy wzoru na pole rombu: P = (e * f) / 2 = (2 m * 3 m) / 2 = 3 m². Odpowiedź: Pole dywanu wynosi 3 m².

Zadanie 4:

Flaga ma kształt trójkąta prostokątnego o przyprostokątnych długości 30 cm i 40 cm. Jakie jest pole tej flagi?

Rozwiązanie: Przyprostokątne w trójkącie prostokątnym to jednocześnie podstawa i wysokość. Zatem P = (a * h) / 2 = (30 cm * 40 cm) / 2 = 600 cm². Odpowiedź: Pole flagi wynosi 600 cm².

Gdzie szukać więcej pomocy?

Jeśli nadal masz trudności, nie zrażaj się! Istnieje wiele zasobów, które mogą Ci pomóc:

• Podręcznik i zeszyt ćwiczeń: To podstawowe źródło wiedzy. Przeczytaj uważnie teorię i spróbuj rozwiązać wszystkie zadania.
• Nauczyciel: Nie bój się zadawać pytań! Nauczyciel jest po to, aby Ci pomóc.
• Korepetycje: Jeśli potrzebujesz indywidualnej pomocy, rozważ skorzystanie z korepetycji.
• Internet: W Internecie znajdziesz mnóstwo materiałów edukacyjnych, filmów instruktażowych i interaktywnych ćwiczeń. Wpisz w wyszukiwarkę "pola figur klasa 5 zadania" i znajdziesz wiele pomocnych stron.
• Gry edukacyjne: Nauka może być zabawą! Poszukaj gier edukacyjnych, które pomogą Ci utrwalić wiedzę o polach figur.

Alternatywne metody nauki

Każdy uczy się inaczej. Jeśli tradycyjne metody nie działają, spróbuj:

• Rysowanie: Rysuj figury i oznaczaj ich wymiary. To pomoże Ci wizualizować problem.
• Wycinanie: Wytnij figury z papieru i spróbuj z nich układać inne figury. To pomoże Ci zrozumieć, jak obliczyć pole.
• Używanie klocków: Użyj klocków, aby zbudować figury i obliczyć ich pole.
• Uczenie kogoś innego: Spróbuj wytłumaczyć komuś innemu, jak obliczyć pole figury. To pomoże Ci utrwalić wiedzę i zidentyfikować obszary, w których masz braki.

Podsumowanie

Obliczanie pól figur to ważna umiejętność, która przydaje się w wielu sytuacjach w życiu. Pamiętaj, że ćwiczenie czyni mistrza. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz wzory i zasady. Nie zrażaj się trudnościami i korzystaj z dostępnych zasobów. Z odrobiną wysiłku geometria przestanie być straszna i stanie się fascynującą dziedziną wiedzy!

Czy ten artykuł pomógł Ci lepiej zrozumieć, jak obliczać pola figur? Jakie inne zagadnienia z matematyki sprawiają Ci trudności i chciałbyś, abyśmy je omówili w przyszłości?