Pola Figur Klasa 5 Sprawdzian

Drogi uczniu klasy 5! Rozumiem, że sprawdzian z pól figur może wywoływać pewien stres. Pamiętam, jak sam się stresowałem przed sprawdzianami z matematyki! Najważniejsze to podejść do tego zadania z pozytywnym nastawieniem i odpowiednim przygotowaniem. Ten artykuł ma na celu pomóc Ci zrozumieć zagadnienia związane z polami figur w sposób prosty i przystępny.

Często zastanawiamy się, po co w ogóle uczyć się o polach figur? Otóż, wiedza ta jest niezwykle przydatna w życiu codziennym. Wyobraź sobie, że chcesz pomalować ścianę w swoim pokoju. Aby obliczyć, ile farby potrzebujesz, musisz znać pole powierzchni ściany. Podobnie, gdy chcesz zasadzić trawnik, musisz wiedzieć, ile trawy kupić, a to zależy od pola powierzchni trawnika.

Podstawowe figury i ich pola

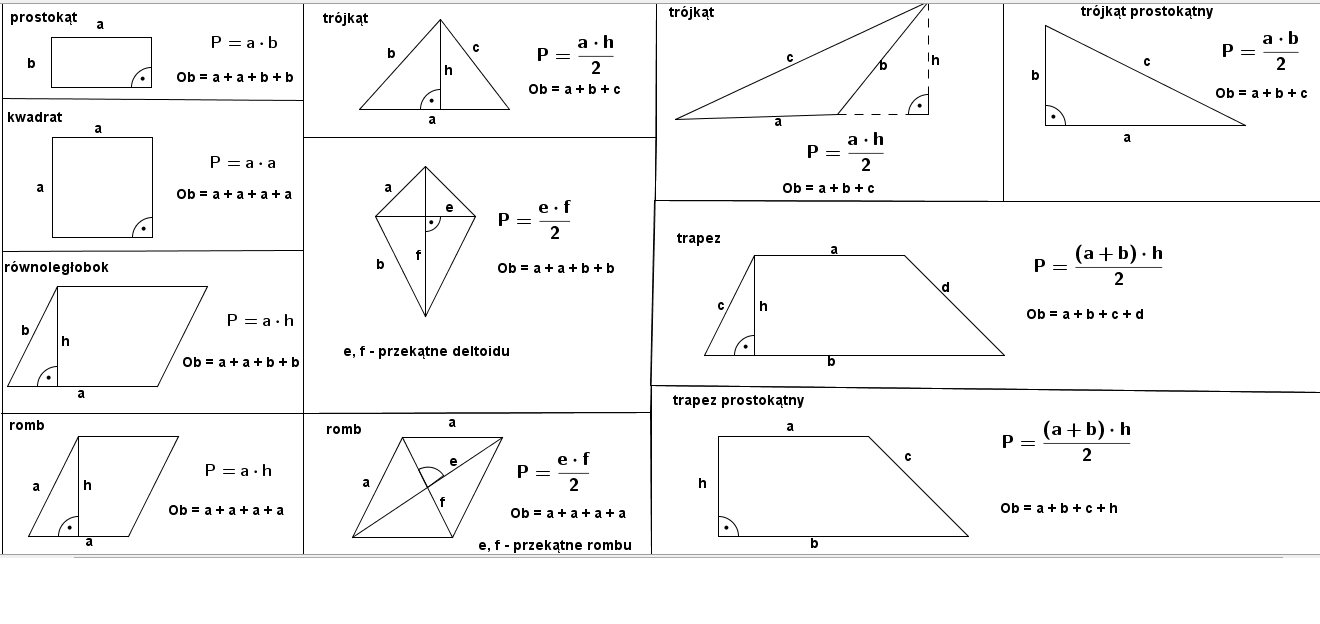
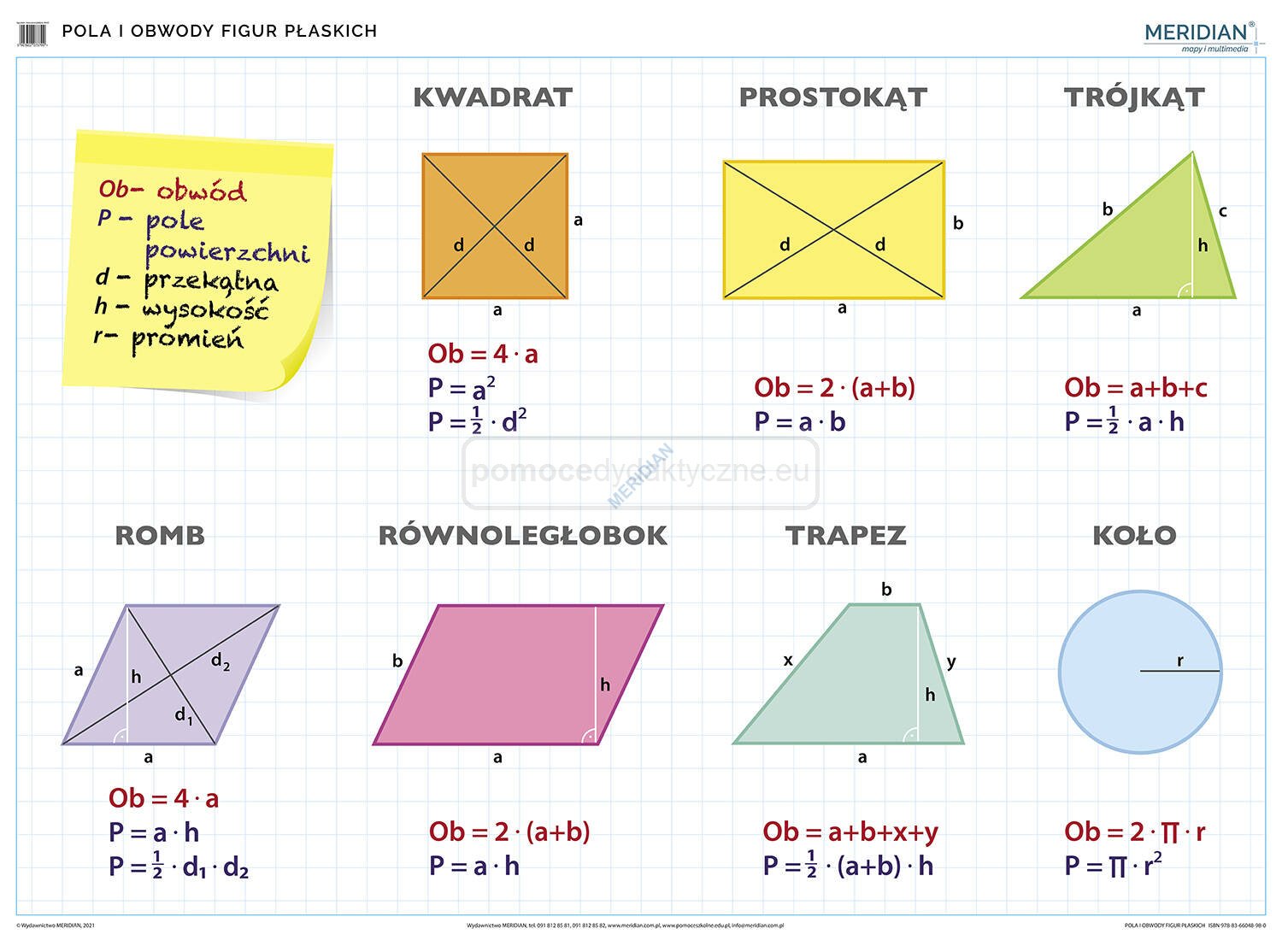
Zacznijmy od przypomnienia sobie podstawowych figur, z którymi spotkasz się na sprawdzianie, i wzorów na obliczanie ich pól.

Prostokąt

Prostokąt to figura, która ma cztery boki i cztery kąty proste. Przeciwległe boki prostokąta są równe.

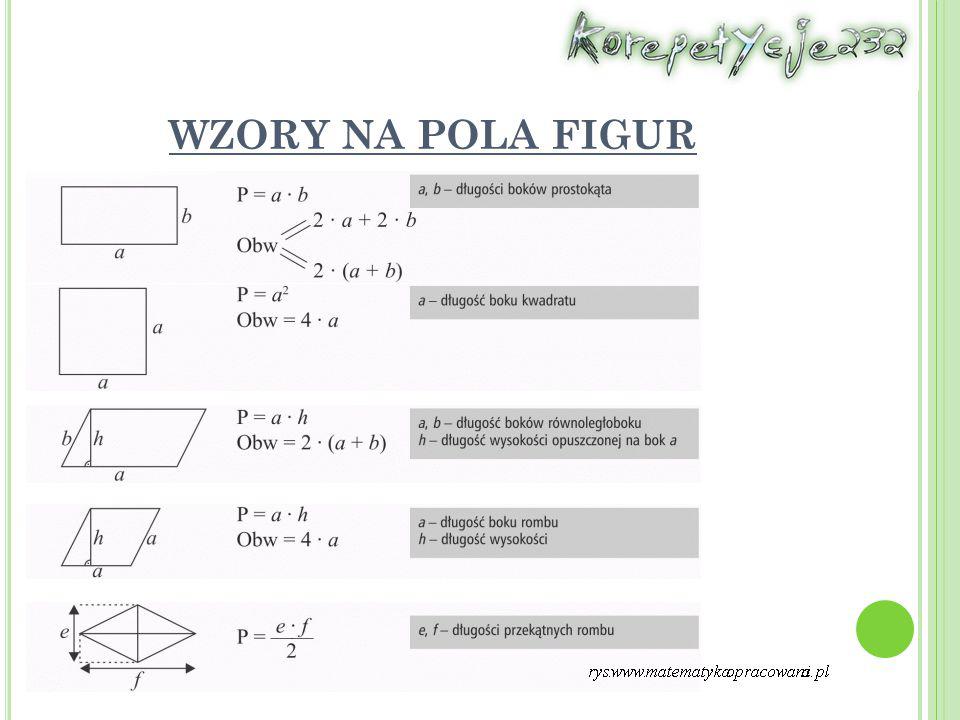
Wzór na pole prostokąta: P = a * b, gdzie:

P - pole prostokąta
a - długość jednego boku
b - długość drugiego boku

Przykład: Jeśli prostokąt ma boki długości 5 cm i 8 cm, to jego pole wynosi P = 5 cm * 8 cm = 40 cm².

Kwadrat

Kwadrat to szczególny rodzaj prostokąta, w którym wszystkie boki są równe.

Wzór na pole kwadratu: P = a², gdzie:

P - pole kwadratu
a - długość boku

Przykład: Jeśli kwadrat ma bok długości 6 cm, to jego pole wynosi P = 6 cm * 6 cm = 36 cm².

Równoległobok

Równoległobok to figura, która ma dwie pary boków równoległych. Przeciwległe boki równoległoboku są równe.

Wzór na pole równoległoboku: P = a * h, gdzie:

P - pole równoległoboku
a - długość podstawy
h - wysokość opuszczona na podstawę (odległość między podstawą a bokiem do niej równoległym)

Przykład: Jeśli równoległobok ma podstawę długości 10 cm, a wysokość opuszczona na tę podstawę wynosi 4 cm, to jego pole wynosi P = 10 cm * 4 cm = 40 cm².

Romb

Romb to szczególny rodzaj równoległoboku, w którym wszystkie boki są równe. Romb ma również dwie przekątne, które przecinają się pod kątem prostym i dzielą się na połowy.

Wzór na pole rombu: P = (e * f) / 2, gdzie:

P - pole rombu
e - długość jednej przekątnej
f - długość drugiej przekątnej

Można również obliczyć pole rombu, używając wzoru na pole równoległoboku: P = a * h, gdzie a to długość boku, a h to wysokość.

Przykład: Jeśli romb ma przekątne długości 8 cm i 6 cm, to jego pole wynosi P = (8 cm * 6 cm) / 2 = 24 cm².

Trójkąt

Trójkąt to figura, która ma trzy boki i trzy kąty.

Wzór na pole trójkąta: P = (a * h) / 2, gdzie:

P - pole trójkąta
a - długość podstawy
h - wysokość opuszczona na podstawę (odległość od wierzchołka do podstawy)

Przykład: Jeśli trójkąt ma podstawę długości 7 cm, a wysokość opuszczona na tę podstawę wynosi 5 cm, to jego pole wynosi P = (7 cm * 5 cm) / 2 = 17.5 cm².

Trapez

Trapez to figura, która ma dwie podstawy równoległe i dwa boki nierównoległe.

Wzór na pole trapezu: P = ((a + b) * h) / 2, gdzie:

P - pole trapezu
a - długość jednej podstawy
b - długość drugiej podstawy
h - wysokość trapezu (odległość między podstawami)

Przykład: Jeśli trapez ma podstawy długości 6 cm i 10 cm, a wysokość wynosi 4 cm, to jego pole wynosi P = ((6 cm + 10 cm) * 4 cm) / 2 = 32 cm².

Typowe zadania na sprawdzianie

Na sprawdzianie możesz spodziewać się różnych typów zadań. Oto kilka przykładów:

Obliczanie pola figury, mając dane długości boków i wysokości.
Obliczanie długości boku lub wysokości, mając dane pole figury i inne wymiary.
Porównywanie pól różnych figur.
Zadania tekstowe, w których musisz zastosować wiedzę o polach figur do rozwiązania problemu praktycznego.
Dzielenie figur na mniejsze, aby obliczyć ich pole.

Przykład zadania: Pokój ma kształt prostokąta o wymiarach 4 m x 5 m. Ile metrów kwadratowych wykładziny potrzeba do pokrycia podłogi?

Rozwiązanie: P = a * b = 4 m * 5 m = 20 m². Potrzeba 20 metrów kwadratowych wykładziny.

Jak się przygotować do sprawdzianu?

Oto kilka wskazówek, które pomogą Ci dobrze przygotować się do sprawdzianu:

Przejrzyj notatki z lekcji. Upewnij się, że rozumiesz wszystkie wzory i definicje.
Rozwiąż zadania z podręcznika. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zagadnienia.
Poproś o pomoc nauczyciela, jeśli masz jakieś trudności. Nie wstydź się pytać!
Pracuj z kolegami i koleżankami. Wspólne rozwiązywanie zadań może być bardzo pomocne.
Wykorzystaj zasoby internetowe. Istnieje wiele stron internetowych i filmów, które mogą pomóc Ci w nauce.
Odpocznij przed sprawdzianem. Wyspany i wypoczęty mózg pracuje lepiej!

Pamiętaj: Regularna praca i systematyczne powtarzanie materiału to klucz do sukcesu. Nie zostawiaj nauki na ostatnią chwilę!

Częste błędy i jak ich unikać

Wiele osób popełnia pewne typowe błędy podczas obliczania pól figur. Ważne jest, aby ich unikać.

Pomylenie wzorów. Upewnij się, że znasz prawidłowe wzory na pole każdej figury.
Używanie niewłaściwych jednostek. Pamiętaj o używaniu odpowiednich jednostek miary (np. cm², m²).
Nieumiejętność odczytywania rysunków. Uważnie analizuj rysunki i upewnij się, że rozumiesz, które wymiary są podane.
Błędy w obliczeniach. Sprawdzaj swoje obliczenia, aby uniknąć błędów arytmetycznych.
Zapominanie o podzieleniu przez 2. Pamiętaj o podzieleniu przez 2 w wzorach na pole trójkąta, rombu i trapezu.

Przykład błędu: Uczeń oblicza pole trójkąta o podstawie 8 cm i wysokości 6 cm, mnożąc tylko podstawę i wysokość (8 cm * 6 cm = 48 cm²) i zapominając o podzieleniu wyniku przez 2. Prawidłowe rozwiązanie to (8 cm * 6 cm) / 2 = 24 cm².

Inne punkty widzenia i rozszerzenia

Niektórzy mogą uważać, że nauka o polach figur jest nudna i niepotrzebna. Jednak, jak wspomniałem na początku, wiedza ta jest bardzo praktyczna i przydaje się w wielu sytuacjach. Ponadto, zrozumienie pojęcia pola powierzchni jest podstawą do dalszej nauki matematyki, na przykład geometrii przestrzennej.

Dla bardziej zaawansowanych uczniów można rozszerzyć wiedzę o polach figur o obliczanie pól figur złożonych, czyli takich, które składają się z kilku prostszych figur. Można również uczyć się o przybliżonym obliczaniu pól figur nieregularnych, na przykład za pomocą siatki kwadratów.

Wykorzystywanie kalkulatorów na sprawdzianie może być kontrowersyjne. Z jednej strony kalkulator ułatwia obliczenia i pozwala uniknąć błędów. Z drugiej strony, używanie kalkulatora może sprawić, że uczniowie nie będą ćwiczyć obliczeń w pamięci i na kartce, co jest również ważne.

Podsumowanie i co dalej?

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć zagadnienia związane z polami figur i przygotować się do sprawdzianu. Pamiętaj, że kluczem do sukcesu jest regularna praca, systematyczne powtarzanie materiału i rozwiązywanie zadań.

Nie bój się wyzwań i podejdź do sprawdzianu z pozytywnym nastawieniem. Wierzę w Ciebie!

Teraz, po przeczytaniu tego artykułu, czy czujesz się pewniej w temacie pól figur? Zachęcam Cię do rozwiązania jeszcze kilku zadań z podręcznika lub ze strony internetowej, aby utrwalić swoją wiedzę.