Pola Czworokątów Zadania Klasa 7

Rozumiem. Siódma klasa to czas, kiedy geometria zaczyna nabierać rumieńców. Te wszystkie definicje, twierdzenia... a w szczególności czworokąty. Pamiętam, sam się z nimi zmagałem! Chciałbym pomóc Ci zrozumieć je lepiej, a przede wszystkim – rozwiązywać zadania.

Zacznijmy od początku. Dlaczego właściwie czworokąty są ważne? To nie tylko suche regułki w podręczniku. Spójrz dookoła! Ekran Twojego komputera lub telefonu, okna w domu, blaty stołów, kafelki... Mnóstwo rzeczy ma kształt czworokątów! Zrozumienie ich właściwości pozwala nam projektować, budować i rozumieć świat wokół nas.

Podstawowe definicje i rodzaje czworokątów

Zanim przejdziemy do zadań, przypomnijmy sobie kilka kluczowych pojęć. Czworokąt to figura geometryczna, która ma cztery boki, cztery kąty i cztery wierzchołki. Ale to dopiero początek!

Podział czworokątów

Czworokąty dzielimy na różne rodzaje, w zależności od ich właściwości:

• Równoległobok: Czworokąt, który ma dwie pary boków równoległych.
• Prostokąt: Równoległobok, który ma wszystkie kąty proste (90 stopni).
• Kwadrat: Prostokąt, który ma wszystkie boki równe.
• Romb: Równoległobok, który ma wszystkie boki równe.
• Trapez: Czworokąt, który ma przynajmniej jedną parę boków równoległych.
• Deltoid: Czworokąt, który ma dwie pary boków sąsiednich równych.

Każdy z tych czworokątów ma swoje unikalne cechy, które wykorzystujemy przy rozwiązywaniu zadań.

Kluczowe właściwości czworokątów

Znamy już rodzaje czworokątów, teraz warto przypomnieć sobie ich najważniejsze właściwości:

• Suma kątów w czworokącie: Zawsze wynosi 360 stopni. To bardzo ważna informacja, która często przydaje się w zadaniach!
• Własności równoległoboków:
  • Przeciwległe boki są równe i równoległe.
  • Przeciwległe kąty są równe.
  • Przekątne przecinają się w połowie.
• Własności prostokątów:
  • Wszystkie kąty są proste.
  • Przekątne są równe i przecinają się w połowie.
• Własności kwadratów:
  • Wszystkie boki są równe.
  • Wszystkie kąty są proste.
  • Przekątne są równe, przecinają się pod kątem prostym i dzielą kąty wewnętrzne na połowy (po 45 stopni).
• Własności rombów:
  • Wszystkie boki są równe.
  • Przekątne przecinają się pod kątem prostym i dzielą kąty wewnętrzne na połowy.
• Własności trapezów:
  • Posiada przynajmniej jedną parę boków równoległych (podstawy).
  • Trapez równoramienny ma równe ramiona i kąty przy podstawie są równe.
• Własności deltoidów:
  • Dwie pary boków sąsiednich są równe.
  • Przekątne przecinają się pod kątem prostym.
  • Jedna z przekątnych dzieli deltoid na dwa przystające trójkąty.

Przykładowe zadania i ich rozwiązania

Teraz przejdźmy do praktyki! Rozwiążemy kilka zadań, krok po kroku, żebyś zobaczył, jak wykorzystywać te właściwości.

Zadanie 1: Równoległobok

W równoległoboku ABCD kąt ABC ma miarę 120 stopni. Oblicz miarę kąta CDA i kąta DAB.

Rozwiązanie:

Wiemy, że w równoległoboku przeciwległe kąty są równe. Zatem kąt CDA = kąt ABC = 120 stopni. Suma kątów w czworokącie wynosi 360 stopni. Zatem kąt DAB + kąt BCD = 360 - 120 - 120 = 120 stopni. Kąt DAB = kąt BCD, więc kąt DAB = 120 / 2 = 60 stopni.

Zadanie 2: Prostokąt

Przekątna prostokąta ma długość 10 cm i tworzy z jednym z boków kąt 30 stopni. Oblicz długość tego boku.

Rozwiązanie:

Mamy prostokąt, więc kąt między bokami jest prosty (90 stopni). Przekątna dzieli prostokąt na dwa trójkąty prostokątne. W jednym z nich mamy kąt 30 stopni, przekątną (hipotenuzę) o długości 10 cm i chcemy obliczyć długość boku przyległego do kąta 30 stopni (przyprostokątną). Używamy funkcji cosinus: cos(30) = bok / przekątna. cos(30) = √3 / 2. Zatem bok = przekątna * cos(30) = 10 * (√3 / 2) = 5√3 cm.

Zadanie 3: Kwadrat

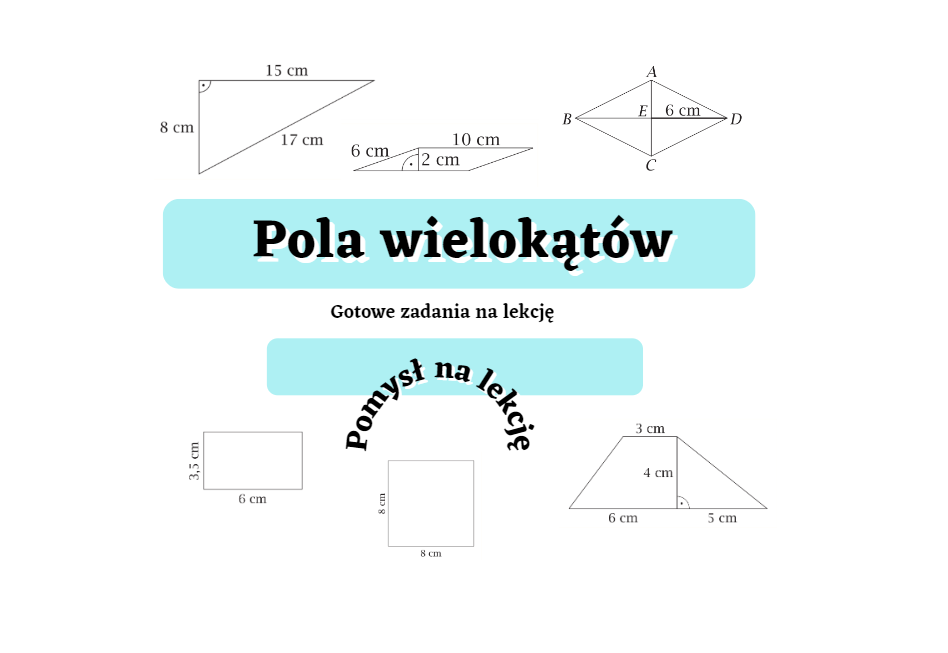
Oblicz pole kwadratu, którego przekątna ma długość 6 cm.

Rozwiązanie:

Przekątna kwadratu dzieli go na dwa trójkąty prostokątne równoramienne. Z twierdzenia Pitagorasa: a² + a² = d², gdzie a to bok kwadratu, a d to przekątna. 2a² = 6². 2a² = 36. a² = 18. Pole kwadratu to a², więc pole = 18 cm².

Zadanie 4: Trapez

W trapezie równoramiennym ABCD podstawy mają długości AB = 10 cm i CD = 6 cm, a wysokość ma długość 4 cm. Oblicz pole tego trapezu.

Rozwiązanie:

Pole trapezu obliczamy ze wzoru: P = (a + b) * h / 2, gdzie a i b to długości podstaw, a h to wysokość. P = (10 + 6) * 4 / 2 = 16 * 4 / 2 = 32 cm².

Typowe trudności i jak sobie z nimi radzić

Wiem, że czasem zadania na czworokąty mogą sprawiać trudności. Oto kilka typowych problemów i sugestii, jak je pokonać:

• Brak zrozumienia definicji: To podstawa! Upewnij się, że naprawdę rozumiesz, czym jest każdy rodzaj czworokąta i jakie ma właściwości. Przeczytaj definicje kilka razy, narysuj sobie przykłady.
• Trudności z identyfikacją czworokąta: Czasem zadanie opisuje czworokąt w sposób nieoczywisty. Spróbuj narysować go na podstawie opisu. Zaznacz na rysunku wszystkie znane informacje (długości boków, miary kątów).
• Brak pomysłu na rozwiązanie: Jeśli nie wiesz, od czego zacząć, spróbuj wypisać wszystkie informacje, które masz w zadaniu. Następnie zastanów się, jakie wzory i twierdzenia mogą się przydać. Czasami pomocne jest dorysowanie dodatkowych linii (np. wysokości, przekątnych).
• Błędy w obliczeniach: Sprawdzaj swoje obliczenia! Używaj kalkulatora, jeśli potrzebujesz. Pamiętaj o jednostkach!

Co, jeśli nie zgadzasz się z odpowiedzią?

Czasami możesz mieć wrażenie, że Twoje rozwiązanie jest poprawne, a jednak odpowiedź w książce mówi co innego. Co wtedy zrobić?

• Sprawdź obliczenia jeszcze raz: Najpierw upewnij się, że nie popełniłeś żadnego błędu rachunkowego.
• Porównaj swoje rozwiązanie z rozwiązaniem nauczyciela lub kolegi: Spróbuj zrozumieć, gdzie popełniłeś błąd.
• Zgłoś się do nauczyciela: Jeśli nadal masz wątpliwości, poproś nauczyciela o pomoc. Wyjaśnij, jak rozwiązywałeś zadanie i dlaczego uważasz, że Twoja odpowiedź jest poprawna.

Pamiętaj, że nauka matematyki to proces. Nie zrażaj się, jeśli nie wszystko od razu rozumiesz. Ważne jest, żeby ćwiczyć i zadawać pytania.

Gdzie szukać dodatkowej pomocy?

Jeśli potrzebujesz dodatkowej pomocy, oto kilka źródeł, które mogą się przydać:

• Podręcznik do matematyki: Zawiera definicje, twierdzenia i przykładowe zadania.
• Zeszyt ćwiczeń: Pozwala na utrwalenie wiedzy i sprawdzenie swoich umiejętności.
• Internet: Znajdziesz tam mnóstwo materiałów edukacyjnych, filmów instruktażowych i interaktywnych ćwiczeń. Poszukaj stron internetowych i kanałów YouTube poświęconych matematyce.
• Korepetytor: Indywidualne lekcje z korepetytorem mogą pomóc Ci zrozumieć trudne zagadnienia i nadrobić zaległości.
• Grupa rówieśnicza: Wspólna nauka z kolegami i koleżankami może być bardzo efektywna. Możecie się nawzajem uczyć i rozwiązywać zadania razem.

Pamiętaj, że kluczem do sukcesu jest regularna praca i zaangażowanie. Im więcej ćwiczysz, tym lepiej będziesz rozumiał czworokąty!

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć czworokąty. Pamiętaj, ćwiczenie czyni mistrza!

Teraz Ty. Zastanów się, który rodzaj czworokąta sprawia Ci najwięcej trudności i spróbuj rozwiązać kilka zadań z nim związanych. Czy po przeczytaniu tego artykułu czujesz się pewniej w rozwiązywaniu zadań z czworokątami?