Podzielność Liczb Klasa 4 Zadania

Witajcie, młodzi matematycy! Dziś zagłębimy się w fascynujący świat podzielności liczb. To temat niezwykle ważny i przydatny, który pomoże Wam lepiej zrozumieć, jak liczby są ze sobą powiązane. Przygotujcie się na solidną dawkę wiedzy, która przyda się nie tylko w klasie 4, ale i w całym Waszym życiu!

Czym jest podzielność liczb?

Podzielność liczb to nic innego jak sprawdzenie, czy jedną liczbę można podzielić przez drugą bez reszty. Reszta to to, co nam zostaje, gdy nie możemy podzielić równo. Mówimy, że liczba A jest podzielna przez liczbę B, jeśli po podzieleniu A przez B otrzymujemy liczbę całkowitą, a reszta wynosi zero. To proste, prawda?

Podzielność przez 2

Zacznijmy od najłatwiejszej zasady – podzielności przez 2. Liczba jest podzielna przez 2, jeśli jej ostatnia cyfra jest parzysta, czyli 0, 2, 4, 6 lub 8. To naprawdę łatwe do zapamiętania! Na przykład:

10 jest podzielne przez 2, bo kończy się na 0.
24 jest podzielne przez 2, bo kończy się na 4.
136 jest podzielne przez 2, bo kończy się na 6.
12345678 jest podzielne przez 2, bo kończy się na 8.
15 nie jest podzielne przez 2, bo kończy się na 5.

Spójrzcie wokół siebie! Ile przedmiotów w Waszej klasie można podzielić na równe pary? Na przykład, jeśli macie 22 krzesła, to można je podzielić na 11 par, bo 22 jest podzielne przez 2.

Podzielność przez 5

Kolejna prosta zasada dotyczy podzielności przez 5. Liczba jest podzielna przez 5, jeśli jej ostatnia cyfra to 0 lub 5. Pamiętajcie o tym, bo to bardzo przydatne!

25 jest podzielne przez 5, bo kończy się na 5.
100 jest podzielne przez 5, bo kończy się na 0.
345 jest podzielne przez 5, bo kończy się na 5.
12345670 jest podzielne przez 5, bo kończy się na 0.
17 nie jest podzielne przez 5, bo kończy się na 7.

Wyobraźcie sobie, że macie 35 cukierków i chcecie podzielić je równo między 5 przyjaciół. Każdy z Was dostanie 7 cukierków, bo 35 jest podzielne przez 5!

Podzielność przez 10

Podzielność przez 10 to pestka! Liczba jest podzielna przez 10, jeśli jej ostatnia cyfra to 0. To chyba najłatwiejsza zasada ze wszystkich.

30 jest podzielne przez 10, bo kończy się na 0.
200 jest podzielne przez 10, bo kończy się na 0.
1234567890 jest podzielne przez 10, bo kończy się na 0.
55 nie jest podzielne przez 10, bo kończy się na 5.

Pomyślcie o pieniądzach. Jeśli macie 100 zł, to możecie je podzielić na 10 banknotów po 10 zł. 100 jest podzielne przez 10!

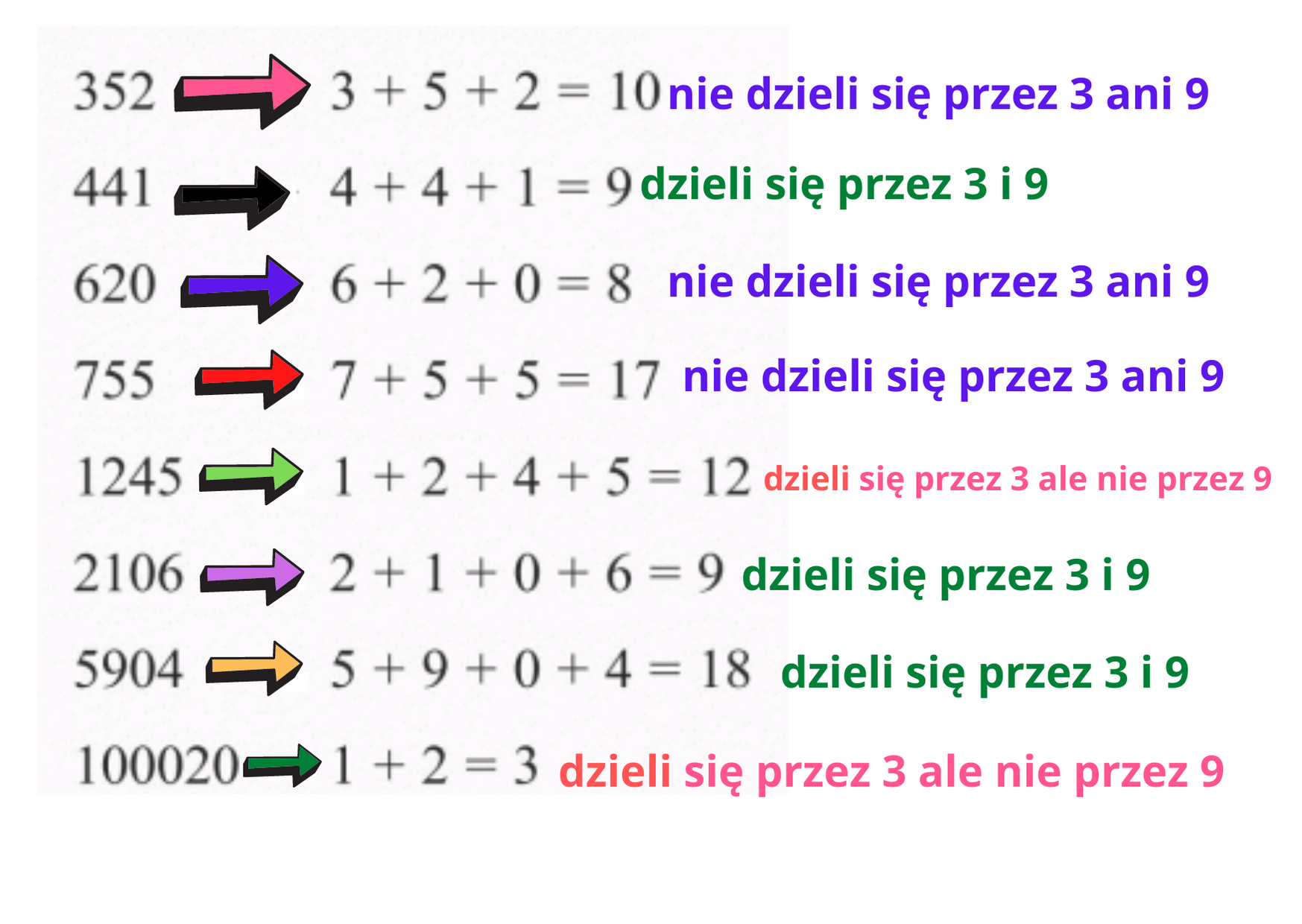
Podzielność przez 3

Podzielność przez 3 jest trochę bardziej skomplikowana, ale spokojnie, poradzimy sobie! Liczba jest podzielna przez 3, jeśli suma jej cyfr jest podzielna przez 3. Spójrzmy na przykład:

12: 1 + 2 = 3, a 3 jest podzielne przez 3, więc 12 jest podzielne przez 3.
27: 2 + 7 = 9, a 9 jest podzielne przez 3, więc 27 jest podzielne przez 3.
123: 1 + 2 + 3 = 6, a 6 jest podzielne przez 3, więc 123 jest podzielne przez 3.
456: 4 + 5 + 6 = 15, a 15 jest podzielne przez 3, więc 456 jest podzielne przez 3.
124: 1 + 2 + 4 = 7, a 7 nie jest podzielne przez 3, więc 124 nie jest podzielne przez 3.

Wyobraźcie sobie, że macie 27 klocków i chcecie zbudować 3 identyczne wieże. Czy się uda? Tak, bo 27 jest podzielne przez 3!

Podzielność przez 4

Aby sprawdzić, czy liczba jest podzielna przez 4, musimy przyjrzeć się jej dwóm ostatnim cyfrom. Liczba jest podzielna przez 4, jeśli liczba utworzona przez jej dwie ostatnie cyfry jest podzielna przez 4. Albo jeśli dwie ostatnie cyfry to 00.

16: Dwie ostatnie cyfry to 16, a 16 jest podzielne przez 4, więc 16 jest podzielne przez 4.
124: Dwie ostatnie cyfry to 24, a 24 jest podzielne przez 4, więc 124 jest podzielne przez 4.
236: Dwie ostatnie cyfry to 36, a 36 jest podzielne przez 4, więc 236 jest podzielne przez 4.
1200: Dwie ostatnie cyfry to 00, więc 1200 jest podzielne przez 4.
125: Dwie ostatnie cyfry to 25, a 25 nie jest podzielne przez 4, więc 125 nie jest podzielne przez 4.

Pomyślcie o godzinach. Każda godzina ma 60 minut. Czy 140 minut to pełna liczba kwadransów? Tak, bo 40 jest podzielne przez 4, więc 140 minut to pełne 35 kwadransów!

Przykłady zadań z podzielności liczb

Teraz sprawdźmy, jak wykorzystać te zasady w praktyce. Oto kilka przykładów zadań:

Zadanie 1: Które z liczb: 15, 22, 30, 47, 55 są podzielne przez 2?

Rozwiązanie: Liczba 22 i 30 są podzielne przez 2, ponieważ kończą się cyframi parzystymi.

Zadanie 2: Które z liczb: 25, 33, 40, 51, 65 są podzielne przez 5?

Rozwiązanie: Liczby 25, 40 i 65 są podzielne przez 5, ponieważ kończą się cyframi 0 lub 5.

Zadanie 3: Które z liczb: 12, 17, 21, 28, 33 są podzielne przez 3?

Rozwiązanie: Liczby 12 (1+2=3), 21 (2+1=3) i 33 (3+3=6) są podzielne przez 3.

Zadanie 4: Czy liczba 132 jest podzielna przez 4?

Rozwiązanie: Tak, ponieważ dwie ostatnie cyfry to 32, a 32 jest podzielne przez 4.

Zadanie 5: Janek ma 45 cukierków. Chce podzielić je równo między 5 kolegów. Czy to możliwe?

Rozwiązanie: Tak, ponieważ 45 jest podzielne przez 5 (45/5 = 9). Każdy kolega dostanie 9 cukierków.

Dlaczego warto znać zasady podzielności?

Znajomość zasad podzielności jest bardzo przydatna w wielu sytuacjach. Pomaga:

Szybciej rozwiązywać zadania matematyczne: Zamiast dzielić w słupku, możesz szybko sprawdzić, czy liczba jest podzielna przez inną.
Upraszczać ułamki: Znając podzielność, łatwiej znajdziesz wspólny dzielnik licznika i mianownika.
Sprawdzać wyniki obliczeń: Jeśli wiesz, że wynik powinien być podzielny przez jakąś liczbę, możesz szybko sprawdzić, czy się nie pomyliłeś.
Planować i organizować: Tak jak widzieliśmy w przykładach z cukierkami i klockami, podzielność pomaga w dzieleniu przedmiotów na równe grupy.

Podzielność w życiu codziennym

Podzielność liczb jest obecna w wielu aspektach naszego życia, nawet jeśli o tym nie myślimy. Przykładowo:

Gotowanie: Kiedy gotujesz według przepisu i musisz zmniejszyć lub zwiększyć porcję, musisz pamiętać o podzielności składników. Jeśli przepis jest na 4 osoby, a chcesz ugotować dla 2, musisz podzielić wszystkie składniki przez 2.
Zakupy: Kiedy kupujesz kilka takich samych produktów, możesz szybko obliczyć, ile zapłacisz, mnożąc cenę jednego produktu przez liczbę produktów. A jeśli masz ograniczony budżet, możesz sprawdzić, czy stać Cię na daną liczbę produktów.
Podróżowanie: Planując podróż, możesz obliczyć, ile czasu zajmie Ci dojazd, dzieląc odległość przez prędkość. Musisz też wiedzieć, ile osób zmieści się w samochodzie, aby podzielić się kosztami paliwa.
Gry i zabawy: Wiele gier i zabaw wymaga dzielenia graczy na równe drużyny. Znajomość zasad podzielności pomoże Ci to zrobić szybko i sprawnie.

Podsumowanie

Gratulacje! Dotarliście do końca tej lekcji o podzielności liczb. Teraz wiecie, jak sprawdzić, czy liczba jest podzielna przez 2, 3, 4, 5 i 10. Pamiętajcie, że ćwiczenie czyni mistrza, więc rozwiązujcie jak najwięcej zadań, aby utrwalić swoją wiedzę.

Zasady podzielności liczb są jak tajny kod, który otwiera drzwi do lepszego zrozumienia matematyki. Im lepiej je poznacie, tym łatwiej będzie Wam radzić sobie z trudniejszymi zagadnieniami. Nie bójcie się zadawać pytań i eksperymentować z liczbami. Matematyka może być fascynującą przygodą!

Spróbujcie teraz znaleźć w swoim otoczeniu przedmioty, których liczbę możecie sprawdzić pod kątem podzielności. Może to być liczba książek na półce, liczba klocków w pudełku, albo liczba osób w Waszej rodzinie. Bawcie się dobrze i pamiętajcie: matematyka jest wszędzie!