Podstawą Ostrosłupa Jest Kwadrat Abcd O Boku Długości 4

Ostrosłup, którego podstawą jest kwadrat ABCD o boku długości 4, stanowi fascynujący obiekt do analizy geometrycznej. Skupimy się na obliczeniach związanych z jego objętością, polem powierzchni oraz specyficznymi właściwościami, w zależności od jego wysokości i kształtu ścian bocznych. Wyobraźmy sobie, że dany ostrosłup ma różne warianty, od prostego ostrosłupa prawidłowego czworokątnego, po bardziej skomplikowane konstrukcje, gdzie wierzchołek ostrosłupa nie leży bezpośrednio nad środkiem kwadratu.

Zacznijmy od podstaw. Mamy kwadrat ABCD o boku długości a = 4. Jego pole powierzchni wynosi zatem P_podstawy = a^2 = 4^2 = 16. To fundamentalna wartość, która będzie nam potrzebna do dalszych obliczeń.

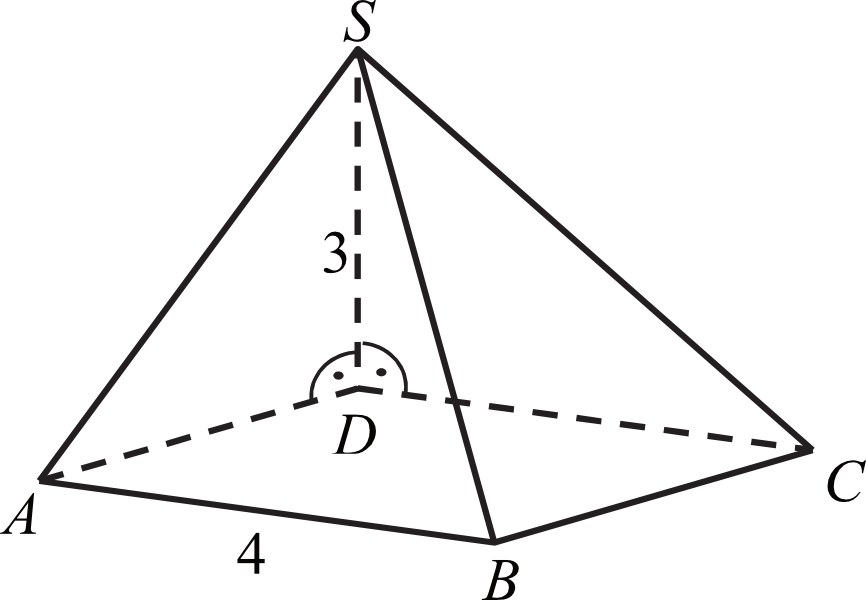
Załóżmy, że mamy do czynienia z ostrosłupem prawidłowym czworokątnym. Oznacza to, że jego podstawą jest kwadrat, a wierzchołek ostrosłupa znajduje się dokładnie nad środkiem tego kwadratu. W tym przypadku wysokość ostrosłupa (H) jest linią prostą łączącą wierzchołek z punktem przecięcia przekątnych kwadratu.

Objętość ostrosłupa (V) obliczamy ze wzoru: V = (1/3) * P_podstawy * H. Zatem, jeśli np. H = 6, to V = (1/3) * 16 * 6 = 32. Objętość wyrażamy w jednostkach sześciennych, np. cm³.

Aby obliczyć pole powierzchni całkowitej ostrosłupa, musimy znać pole powierzchni podstawy (które już mamy) oraz pole powierzchni ścian bocznych. W ostrosłupie prawidłowym czworokątnym, ściany boczne są identycznymi trójkątami równoramiennymi. Aby obliczyć pole jednego trójkąta, potrzebujemy znać długość podstawy (która jest równa bokowi kwadratu, czyli 4) oraz wysokość tego trójkąta (h). Wysokość trójkąta nazywamy wysokością ściany bocznej.

Wysokość ściany bocznej (h) możemy obliczyć za pomocą twierdzenia Pitagorasa. Tworzymy trójkąt prostokątny, którego przyprostokątnymi są połowa długości boku kwadratu (a/2 = 2) oraz wysokość ostrosłupa (H), a przeciwprostokątną jest właśnie wysokość ściany bocznej (h). Zatem: h^2 = (a/2)^2 + H^2. Jeśli H = 6, to h^2 = 2^2 + 6^2 = 4 + 36 = 40. Zatem h = √40 = 2√10.

Pole jednej ściany bocznej wynosi P_ściany = (1/2) * a * h = (1/2) * 4 * 2√10 = 4√10. Ponieważ mamy cztery ściany boczne, to pole powierzchni bocznej wynosi P_boczne = 4 * P_ściany = 4 * 4√10 = 16√10.

Pole powierzchni całkowitej ostrosłupa (P_całkowite) wynosi zatem P_całkowite = P_podstawy + P_boczne = 16 + 16√10.

Różne wysokości i kąty nachylenia ścian

Analizując ostrosłupy, kluczowe jest zrozumienie zależności między wysokością, kątami nachylenia ścian bocznych do podstawy oraz długościami krawędzi bocznych. Zmieniając wysokość ostrosłupa, wpływamy na kąty nachylenia ścian bocznych i długość krawędzi bocznych. Im większa wysokość, tym bardziej strome są ściany boczne i dłuższe krawędzie boczne. Im mniejsza wysokość, tym ściany boczne są bardziej "płaskie" a krawędzie boczne krótsze.

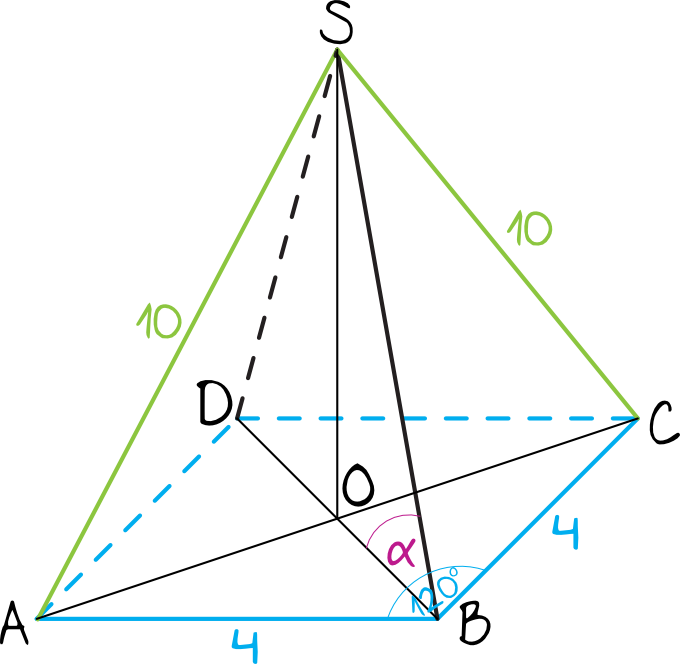
Kąt nachylenia ściany bocznej do podstawy (α) możemy obliczyć korzystając z funkcji trygonometrycznych. Tangens tego kąta (tg α) jest równy stosunkowi wysokości ostrosłupa (H) do połowy długości boku podstawy (a/2). Zatem tg α = H / (a/2). Jeśli H = 6, to tg α = 6 / 2 = 3. Zatem α = arctg(3).

Długość krawędzi bocznej (k) również możemy obliczyć za pomocą twierdzenia Pitagorasa. Tworzymy trójkąt prostokątny, którego przyprostokątnymi są wysokość ostrosłupa (H) oraz połowa długości przekątnej kwadratu podstawy (d/2), a przeciwprostokątną jest krawędź boczna (k). Długość przekątnej kwadratu wynosi d = a√2 = 4√2. Zatem d/2 = 2√2. Mamy więc k^2 = H^2 + (d/2)^2 = H^2 + (2√2)^2. Jeśli H = 6, to k^2 = 6^2 + (2√2)^2 = 36 + 8 = 44. Zatem k = √44 = 2√11.

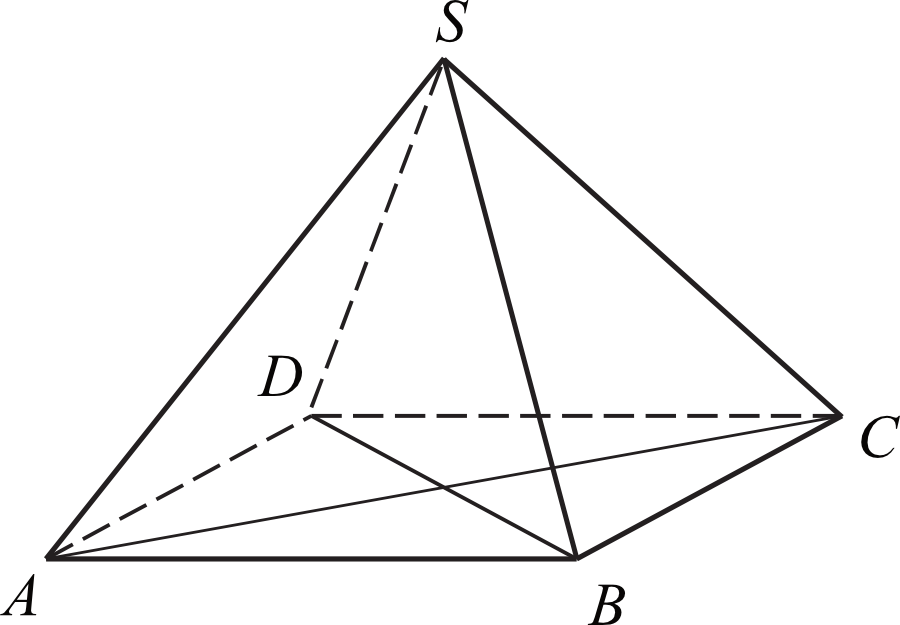
Jeśli wierzchołek ostrosłupa nie leży bezpośrednio nad środkiem kwadratu, obliczenia stają się bardziej skomplikowane. W takim przypadku musimy znać dokładne współrzędne wierzchołka, aby móc obliczyć długości krawędzi bocznych i wysokości ścian bocznych. W takim przypadku, ściany boczne nie będą już identycznymi trójkątami równoramiennymi, a obliczenie ich pól powierzchni będzie wymagało użycia wzoru Herona lub innych metod.

Obliczenia bardziej skomplikowanych wariantów

Rozważmy sytuację, w której wierzchołek ostrosłupa znajduje się nad jednym z wierzchołków podstawy. To oznacza, że jedna z krawędzi bocznych ma długość zero (ściśle mówiąc, zlewa się z krawędzią podstawy), a ostrosłup jest mocno "przechylony". W takim przypadku, obliczenie objętości nadal jest możliwe, ale wymaga innego podejścia do określenia wysokości ostrosłupa. Wysokość ostrosłupa jest teraz odległością od wierzchołka do płaszczyzny podstawy, mierzona prostopadle do tej płaszczyzny.

Aby obliczyć pole powierzchni całkowitej, musimy obliczyć pola powierzchni poszczególnych ścian bocznych. Ściany boczne będą teraz trójkątami o różnych długościach boków, więc będziemy musieli skorzystać z wzoru Herona, aby obliczyć ich pola. Wzór Herona mówi, że pole trójkąta o bokach a, b, c wynosi P = √(s(s-a)(s-b)(s-c)), gdzie s to połowa obwodu trójkąta, czyli s = (a+b+c)/2.

Załóżmy, że wierzchołek ostrosłupa (W) leży nad wierzchołkiem A kwadratu ABCD. Wtedy krawędzie boczne mają długości: WA = H, WB = √(H^2 + a^2), WC = √(H^2 + 2a^2), WD = √(H^2 + a^2). Ściany boczne to trójkąty: ΔWAB, ΔWBC, ΔWCD, ΔWDA. Do obliczenia pól tych trójkątów potrzebujemy znać długości wszystkich ich boków, a następnie zastosować wzór Herona.

Obliczenia stają się jeszcze bardziej złożone, jeśli wierzchołek ostrosłupa nie leży nad żadnym charakterystycznym punktem podstawy (środkiem, wierzchołkiem, środkiem boku). W takim przypadku potrzebujemy znać współrzędne wszystkich punktów (A, B, C, D, W) w przestrzeni trójwymiarowej. Następnie możemy obliczyć długości wszystkich krawędzi i wysokości ścian bocznych, a następnie obliczyć pola powierzchni poszczególnych ścian i sumować je, aby uzyskać pole powierzchni całkowitej.

Zastosowania w praktyce

Rozważania nad ostrosłupami o podstawie kwadratowej mają szerokie zastosowanie w praktyce, od architektury po inżynierię. Piramidy egipskie są doskonałym przykładem zastosowania ostrosłupów o podstawie kwadratowej w architekturze. W inżynierii, ostrosłupy mogą być wykorzystywane jako elementy konstrukcyjne mostów lub dachów. Zrozumienie właściwości geometrycznych ostrosłupów jest kluczowe do projektowania stabilnych i efektywnych struktur.

Ponadto, obliczenia związane z objętością i polem powierzchni ostrosłupów są ważne w wielu dziedzinach, takich jak logistyka (obliczanie pojemności magazynów o nietypowym kształcie) czy produkcja (optymalizacja zużycia materiałów przy produkcji elementów o kształcie ostrosłupa).

Wszystkie te przykłady pokazują, że geometria ostrosłupa o podstawie kwadratowej, choć na pierwszy rzut oka prosta, kryje w sobie wiele interesujących i praktycznych zagadnień. Rozwiązując zadania z ostrosłupami, ćwiczymy umiejętność logicznego myślenia, przestrzennej wyobraźni i stosowania twierdzeń matematycznych w praktyce.