Podstawą Graniastosłupa Prostego Jest Trapez Równoramienny

Graniastosłup prosty, którego podstawą jest trapez równoramienny, to fascynujący obiekt w geometrii przestrzennej. Łączy w sobie regularność bryły z subtelnością figury płaskiej, dając nam wiele możliwości do rozważań i obliczeń. Przyjrzyjmy się bliżej tej strukturze.

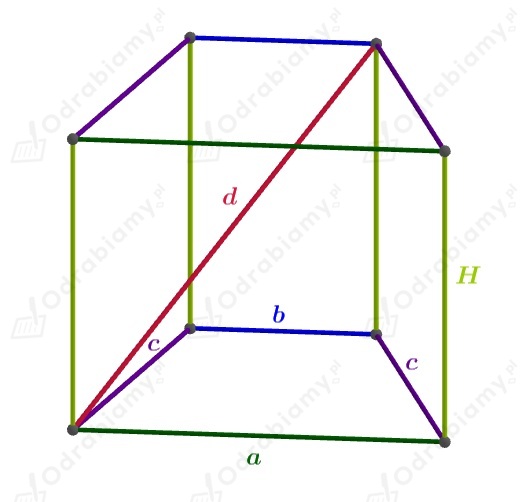
Wyobraźmy sobie, że mamy trapez równoramienny. Charakterystyczne dla niego jest to, że jego ramiona mają taką samą długość, a kąty przy każdej z podstaw są równe. Teraz, wyobraźmy sobie, że ten trapez staje się podstawą prostopadłościanu. To właśnie jest nasz graniastosłup prosty o podstawie w kształcie trapezu równoramiennego. "Prosty" oznacza, że ściany boczne graniastosłupa są prostokątami i są prostopadłe do płaszczyzny podstawy.

Zacznijmy od analizy pola powierzchni. Pole powierzchni całkowitej takiego graniastosłupa składa się z dwóch pól podstaw (identyczne trapezy równoramienne) i pól powierzchni ścian bocznych (cztery prostokąty).

Aby obliczyć pole podstawy, potrzebujemy znać długości podstaw trapezu (oznaczmy je jako a i b) oraz wysokość trapezu (h). Pole trapezu obliczamy według wzoru: P_podstawy = (a + b) * h / 2. Mnożymy wynik razy dwa, ponieważ mamy dwie takie podstawy.

Teraz przechodzimy do ścian bocznych. Mamy dwie ściany boczne, które są prostokątami o wymiarach "długość ramienia trapezu" (oznaczmy je jako c) i "wysokość graniastosłupa" (oznaczmy je jako H). Pole każdej z tych ścian wynosi c * H. Mamy również dwie ściany boczne, które są prostokątami o wymiarach "długość podstawy trapezu a" i "wysokość graniastosłupa H" (pole a * H) oraz "długość podstawy trapezu b" i "wysokość graniastosłupa H" (pole b * H).

Sumując to wszystko, pole powierzchni całkowitej graniastosłupa prostego o podstawie w kształcie trapezu równoramiennego wynosi: P_całkowite = 2 * ((a + b) * h / 2) + 2 * (c * H) + a * H + b * H = (a + b) * h + 2 * c * H + a * H + b * H = (a + b) * h + H * (2c + a + b).

Przejdźmy do obliczania objętości. Objętość graniastosłupa liczymy mnożąc pole podstawy przez wysokość graniastosłupa. W naszym przypadku, objętość V = P_podstawy * H = ((a + b) * h / 2) * H = (a + b) * h * H / 2.

Własności i Zastosowania

Graniastosłup prosty o podstawie w kształcie trapezu równoramiennego, poza swoimi podstawowymi parametrami geometrycznymi, posiada pewne ciekawe własności. Ze względu na symetrię trapezu równoramiennego, bryła ta ma pewną dozę elegancji. W praktycznych zastosowaniach, choć może nie tak powszechna jak prostopadłościan, znajduje swoje miejsce.

Wyobraźmy sobie architekturę. Elementy dekoracyjne budynków, kolumny z nietypowymi zdobieniami, mogą być inspirowane właśnie tą formą. W inżynierii, fragmenty mostów lub inne konstrukcje mogą wykorzystywać podobne kształty dla uzyskania odpowiedniej wytrzymałości i estetyki.

W projektowaniu przedmiotów codziennego użytku, graniastosłup z trapezem równoramiennym jako podstawą może być elementem lamp, pojemników, czy nawet mebli. Jego nietypowy kształt może dodać charakteru i odróżnić dany przedmiot od innych.

Rozważmy teraz kilka konkretnych przykładów liczbowych, aby lepiej zrozumieć obliczenia.

Przykład 1: Załóżmy, że trapez równoramienny ma podstawy o długości a = 5 cm, b = 10 cm, wysokość h = 4 cm, a ramię ma długość c = 5 cm. Wysokość graniastosłupa wynosi H = 8 cm.

Pole podstawy: P_podstawy = (5 + 10) * 4 / 2 = 15 * 4 / 2 = 30 cm². Pole powierzchni całkowitej: P_całkowite = (5 + 10) * 4 + 8 * (2 * 5 + 5 + 10) = 60 + 8 * (10 + 5 + 10) = 60 + 8 * 25 = 60 + 200 = 260 cm². Objętość: V = (5 + 10) * 4 * 8 / 2 = 15 * 4 * 8 / 2 = 15 * 16 = 240 cm³.

Przykład 2: Trapez równoramienny ma podstawy o długości a = 3 cm, b = 7 cm, wysokość h = 2 cm, a ramię ma długość c = 2.5 cm. Wysokość graniastosłupa wynosi H = 6 cm.

Pole podstawy: P_podstawy = (3 + 7) * 2 / 2 = 10 * 2 / 2 = 10 cm². Pole powierzchni całkowitej: P_całkowite = (3 + 7) * 2 + 6 * (2 * 2.5 + 3 + 7) = 20 + 6 * (5 + 3 + 7) = 20 + 6 * 15 = 20 + 90 = 110 cm². Objętość: V = (3 + 7) * 2 * 6 / 2 = 10 * 2 * 6 / 2 = 10 * 6 = 60 cm³.

Relacje z Innymi Figurami

Warto zauważyć, że graniastosłup prosty o podstawie w kształcie trapezu równoramiennego ma pewne powiązania z innymi figurami geometrycznymi. Jeżeli podstawy trapezu (a i b) są sobie równe (a = b), to trapez staje się prostokątem, a graniastosłup staje się prostopadłościanem. Jest to szczególny przypadek graniastosłupa o podstawie trapezoidalnej.

Jeżeli dodatkowo wysokość trapezu (h) równa się długości boku (a = b = h), to trapez staje się kwadratem, a graniastosłup staje się sześcianem, jeśli wysokość H graniastosłupa także będzie równa a.

Ponadto, możemy rozłożyć trapez równoramienny na prostokąt i dwa trójkąty prostokątne. Ta dekompozycja może być pomocna przy obliczeniach pola i obwodu, szczególnie gdy nie znamy wysokości trapezu, ale znamy długość ramienia i podstawy.

Analiza graniastosłupa prostego o podstawie w kształcie trapezu równoramiennego pozwala nam na ćwiczenie umiejętności przestrzennego myślenia oraz na zastosowanie wiedzy z geometrii płaskiej w kontekście brył. Obliczenia pól powierzchni i objętości, choć wymagają pewnej precyzji, są doskonałym sposobem na utrwalenie wzorów i zasad geometrii.

Rozważając ten specyficzny graniastosłup, dostrzegamy, jak geometria łączy się ze światem rzeczywistym, inspirując projektantów, architektów i inżynierów do tworzenia pięknych i funkcjonalnych obiektów.