Podobienstwo Figur Matematyka Wokol Nas Sprawdzian

Czy kiedykolwiek zastanawiałeś się, dlaczego niektóre budynki wydają się tak harmonijne, a inne nie? Albo dlaczego projektanci mody potrafią tworzyć ubrania, które idealnie podkreślają sylwetkę? Odpowiedź, często ukryta, tkwi w matematyce, a konkretnie w koncepcji podobieństwa figur. To nie tylko sucha teoria z podręczników, ale fundament, który kształtuje świat wokół nas.

Podobieństwo Figur: Co to Tak Naprawdę Oznacza?

Na pierwszy rzut oka, "podobieństwo figur" może brzmieć jak skomplikowany termin. Ale w gruncie rzeczy, chodzi o relację między dwoma lub więcej figurami, które mają identyczny kształt, ale mogą różnić się rozmiarem. Wyobraź sobie zdjęcie swojego domu, a potem miniaturkę tego samego zdjęcia. Obie fotografie przedstawiają ten sam dom, ale w różnej skali – są podobne.

Kluczowe Elementy Podobieństwa

Odpowiednie kąty są równe: To fundamentalna zasada. Jeśli dwie figury są podobne, to miary odpowiadających sobie kątów muszą być identyczne.
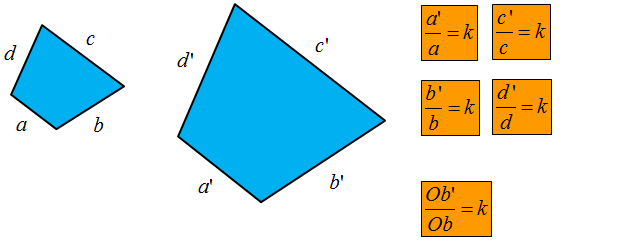
Odpowiednie boki są proporcjonalne: Oznacza to, że stosunek długości odpowiadających sobie boków jest stały. Ten stosunek nazywamy skalą podobieństwa.

Jeśli te dwa warunki są spełnione, możemy śmiało powiedzieć, że figury są podobne. Ale gdzie w życiu codziennym możemy znaleźć przykłady tej koncepcji?

Matematyka Wokół Nas: Przykłady Podobieństwa Figur

Podobieństwo figur nie jest abstrakcyjnym konceptem – jest wszechobecne. Oto kilka przykładów, które pozwolą Ci dostrzec matematykę w otaczającym Cię świecie:

Architektura i Inżynieria

Architekci i inżynierowie wykorzystują podobieństwo figur na każdym etapie projektowania. Tworzą modele budynków, które są podobne do rzeczywistych konstrukcji, ale w znacznie mniejszej skali. Pozwala im to na analizę projektu, identyfikację potencjalnych problemów i optymalizację konstrukcji przed rozpoczęciem budowy. Rzuty budynków, mapy, plany zagospodarowania przestrzennego – wszystko to opiera się na zasadach podobieństwa.

Kartografia

Mapy są doskonałym przykładem zastosowania podobieństwa figur. Mapa świata jest podobna do rzeczywistego globu, ale w znacznie mniejszej skali. Dzięki skali mapy możemy przeliczyć odległości i powierzchnie na mapie na odpowiadające im wartości w rzeczywistości.

Fotografia i Grafika Komputerowa

Robienie zdjęć, skalowanie obrazów w programach graficznych, tworzenie animacji 3D – wszystko to opiera się na zasadach podobieństwa. Kiedy powiększasz zdjęcie, zachowujesz jego proporcje (przynajmniej w teorii idealnego skalowania), co oznacza, że otrzymujesz figurę podobną do oryginału.

Moda i Projektowanie Ubrań

Projektanci mody wykorzystują podobieństwo figur do tworzenia ubrań, które idealnie pasują do różnych typów sylwetek. Wykroje są tworzone w oparciu o proporcje ludzkiego ciała i są skalowane w zależności od rozmiaru ubrania. Dzięki temu ubranie w rozmiarze S jest podobne do ubrania w rozmiarze L, ale w innej skali.

Modele i Zabawki

Modele samochodów, samolotów, statków – wszystkie te przedmioty są podobne do swoich rzeczywistych odpowiedników. Są to po prostu mniejsze, wierne repliki, które pozwalają nam na podziwianie skomplikowanych konstrukcji w przystępnej formie.

Sprawdzian Wiedzy: Przykładowe Zadania i Wyzwania

Jak sprawdzić, czy naprawdę rozumiesz koncepcję podobieństwa figur? Spróbuj rozwiązać kilka prostych zadań:

Zadanie 1: Dwa trójkąty są podobne. Boki pierwszego trójkąta mają długości 3, 4 i 5 cm. Najdłuższy bok drugiego trójkąta ma długość 10 cm. Oblicz długości pozostałych boków drugiego trójkąta.
Zadanie 2: Na mapie w skali 1:1000 odległość między dwoma punktami wynosi 5 cm. Jaka jest rzeczywista odległość między tymi punktami?
Zadanie 3: Prostokąt o wymiarach 2 cm x 4 cm jest podobny do prostokąta o wymiarach 6 cm x 12 cm. Jaka jest skala podobieństwa?

Rozwiązanie tych zadań pomoże Ci utrwalić wiedzę i sprawdzić, czy potrafisz zastosować zasady podobieństwa w praktyce.

Adresowanie Kontrargumentów: Czy Podobieństwo Zawsze Jest Idealne?

Warto zauważyć, że w realnym świecie idealne podobieństwo jest trudne do osiągnięcia. Nawet w najbardziej precyzyjnych modelach i odwzorowaniach zawsze występują pewne odchylenia i uproszczenia. Na przykład, mapa świata, która idealnie odwzorowywałaby powierzchnię Ziemi, musiałaby być w formie globu. Każde spłaszczenie globu na płaską powierzchnię powoduje pewne zniekształcenia. Podobnie, ubrania w różnych rozmiarach mogą nie być idealnie podobne ze względu na różnice w proporcjach ludzkiego ciała.

Jednak pomimo tych ograniczeń, koncepcja podobieństwa figur jest niezwykle użyteczna i praktyczna. Pozwala nam na modelowanie rzeczywistości, przewidywanie zachowań obiektów i rozwiązywanie problemów inżynieryjnych i projektowych.

Rozwiązania, a nie tylko Problemy: Wykorzystaj Wiedzę o Podobieństwie

Zamiast traktować podobieństwo figur jako kolejną definicję do zapamiętania, spróbuj dostrzec jego praktyczne zastosowania. Pomyśl o tym, jak możesz wykorzystać tę wiedzę w swoich własnych projektach, hobby lub zainteresowaniach. Może chcesz stworzyć model swojej ulubionej budowli, zaprojektować własną odzież lub zrozumieć, jak działają mapy i globusy. Koncepcja podobieństwa figur otwiera przed Tobą wiele możliwości.

Dodatkowo, zrozumienie podobieństwa figur rozwija myślenie przestrzenne i logiczne, co jest niezwykle przydatne w wielu dziedzinach życia, od nauki po sztukę.

Podsumowanie: Co Dalej?

Podobieństwo figur to fascynujący i wszechobecny koncept matematyczny, który wpływa na wiele aspektów naszego życia. Od architektury po modę, od map po modele, zasady podobieństwa są wykorzystywane do tworzenia, analizowania i rozumienia świata wokół nas.

Mam nadzieję, że ten artykuł pomógł Ci dostrzec matematykę w otaczającej Cię rzeczywistości i zachęcił do dalszego zgłębiania tej fascynującej dziedziny. Czy dostrzegasz teraz przykłady podobieństwa figur w swoim codziennym życiu? Zachęcam Cię do aktywnego poszukiwania i eksperymentowania! Może nawet spróbujesz stworzyć własny model lub mapę, wykorzystując zdobytą wiedzę.