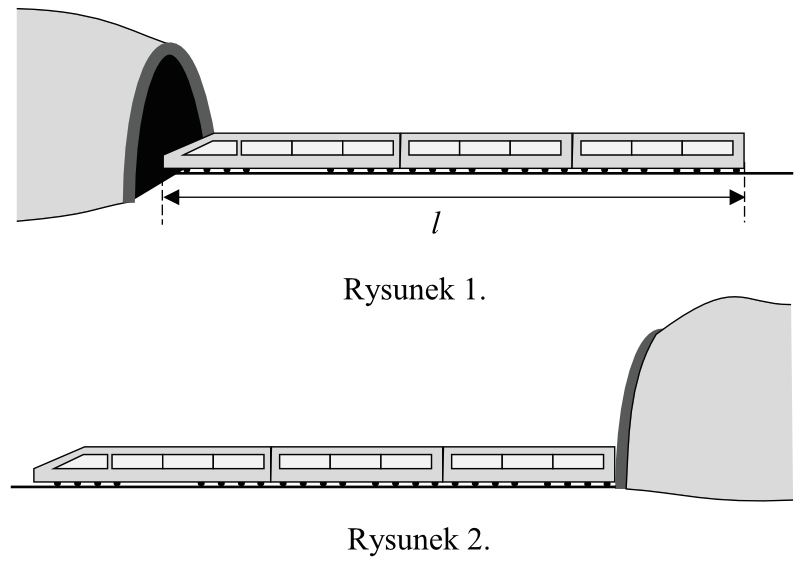
Pociąg Jadący Ze Stałą Prędkością Przejechał Most Długości 200 M

Pociąg, majestatyczny stalowy kolos sunący po żelaznych szynach, to od wieków symbol podróży, postępu i nieustannego dążenia do celu. Wyobraźmy sobie taki pociąg, pędzący ze stałą, niezmienną prędkością, przecinający krajobraz. Przed nim wyrasta most, konstrukcja inżynieryjna spinająca dwa brzegi, rozpięta nad doliną, rzeką lub innym przeszkodą. Ten konkretny most ma długość 200 metrów. Zastanówmy się, co możemy wywnioskować z tej sytuacji, jak opisać ruch pociągu i jakie obliczenia możemy przeprowadzić, aby lepiej zrozumieć to zjawisko.

Zacznijmy od podstawowych założeń. Pociąg porusza się ze stałą prędkością. Oznacza to, że jego prędkość w każdym momencie podróży jest taka sama. Nie przyspiesza, nie zwalnia, po prostu utrzymuje konstantną wartość. To upraszcza nasze rozważania, ponieważ możemy uniknąć skomplikowanych równań związanych z ruchem zmiennym.

Rozważmy moment, w którym lokomotywa pociągu wjeżdża na most. W tym momencie zaczynamy mierzyć czas. Pociąg zaczyna pokonywać kolejne metry konstrukcji. Mijają sekundy, a kolejne wagony wjeżdżają na most. Kiedy ostatni wagon pociągu opuszcza most, odnotowujemy czas, który upłynął. To jest kluczowa informacja.

Jednak aby w pełni opisać sytuację, musimy znać jeszcze jedną wartość: długość pociągu. Bez tej wiedzy nie będziemy mogli dokładnie obliczyć prędkości, z jaką porusza się pociąg. Nazwijmy długość pociągu "L".

Zatem, aby pociąg całkowicie przejechał przez most, musi pokonać dystans równy sumie długości mostu i długości pociągu. Innymi słowy, pociąg musi pokonać 200 metrów (długość mostu) plus L metrów (długość pociągu). Całkowity dystans to 200 + L metrów.

Załóżmy, że czas, w którym pociąg pokonuje most, wynosi "t" sekund. Teraz mamy wszystkie dane potrzebne do obliczenia prędkości.

Prędkość pociągu (v) jest równa dystansowi (d) podzielonemu przez czas (t). W naszym przypadku:

v = (200 + L) / t

Wzór ten pozwala nam obliczyć prędkość pociągu, jeśli znamy długość pociągu (L) i czas przejazdu przez most (t).

Co jednak, jeśli nie znamy długości pociągu, ale znamy jego prędkość i czas przejazdu przez most? Wtedy możemy przekształcić wzór i obliczyć długość pociągu:

L = v * t - 200

W tym przypadku, znając prędkość pociągu (v) i czas przejazdu przez most (t), możemy obliczyć jego długość (L).

Rozważmy przykład. Załóżmy, że pociąg porusza się z prędkością 20 metrów na sekundę (v = 20 m/s) i potrzebuje 15 sekund, aby przejechać przez most (t = 15 s). Wtedy długość pociągu wynosi:

L = 20 * 15 - 200 = 300 - 200 = 100 metrów.

Zatem w tym przypadku długość pociągu wynosi 100 metrów.

A co jeśli znamy czas przejazdu tylko lokomotywy przez most? To zmienia naszą perspektywę. Załóżmy, że lokomotywa potrzebuje 10 sekund, aby przejechać przez most o długości 200 metrów. W takim przypadku możemy obliczyć prędkość pociągu:

v = 200 / 10 = 20 m/s

Teraz znamy prędkość pociągu. Jeśli dodatkowo znamy czas, w którym cały pociąg przejeżdża przez most (na przykład 15 sekund), możemy obliczyć długość pociągu, jak już wcześniej pokazałem.

Zależność Długości Pociągu od Czasu i Prędkości

Analizując powyższe wzory, możemy dostrzec bezpośrednią zależność między długością pociągu, jego prędkością i czasem przejazdu przez most. Im większa prędkość pociągu, tym większy dystans pokonuje on w danym czasie, a co za tym idzie, przy stałym czasie przejazdu przez most, może on być dłuższy. Podobnie, im dłuższy czas przejazdu przez most przy stałej prędkości, tym dłuższy może być pociąg. Te zależności są kluczowe w zrozumieniu dynamiki tego problemu.

Możemy również rozważyć sytuację, w której mamy dwa pociągi, każdy o innej długości, przejeżdżające przez ten sam most ze stałą prędkością. Załóżmy, że pierwszy pociąg ma długość L1 i przejeżdża przez most w czasie t1, a drugi pociąg ma długość L2 i przejeżdża przez most w czasie t2. Oba pociągi poruszają się z tą samą prędkością (v).

W takim przypadku możemy zapisać następujące równania:

v = (200 + L1) / t1 v = (200 + L2) / t2

Ponieważ prędkości są równe, możemy je porównać:

(200 + L1) / t1 = (200 + L2) / t2

Z tego równania możemy wywnioskować relację między długościami pociągów a czasami przejazdu. Na przykład, jeśli znamy L1, t1 i t2, możemy obliczyć L2:

L2 = ((200 + L1) * t2 / t1) - 200

To pokazuje, jak możemy wykorzystać informacje o jednym pociągu, aby wywnioskować informacje o drugim pociągu, poruszającym się z tą samą prędkością.

Wyobraźmy sobie, że pierwszy pociąg ma długość 50 metrów i przejeżdża przez most w 12 sekund. Drugi pociąg przejeżdża przez most w 14 sekund. Obliczmy długość drugiego pociągu:

L2 = ((200 + 50) * 14 / 12) - 200 = (250 * 14 / 12) - 200 = (3500 / 12) - 200 ≈ 291.67 - 200 ≈ 91.67 metrów.

Zatem długość drugiego pociągu wynosi około 91.67 metrów.

Podsumowując, analiza ruchu pociągu przejeżdżającego przez most ze stałą prędkością wymaga uwzględnienia długości mostu, długości pociągu oraz czasu przejazdu. Poprzez zastosowanie prostych wzorów fizycznych, możemy obliczyć prędkość pociągu, jego długość lub relacje między różnymi pociągami. Zrozumienie tych zależności pozwala na lepsze zrozumienie dynamiki ruchu i zastosowanie tych zasad w bardziej skomplikowanych problemach fizycznych. Analiza takich prostych sytuacji stanowi doskonałe wprowadzenie do bardziej zaawansowanych zagadnień z zakresu mechaniki.