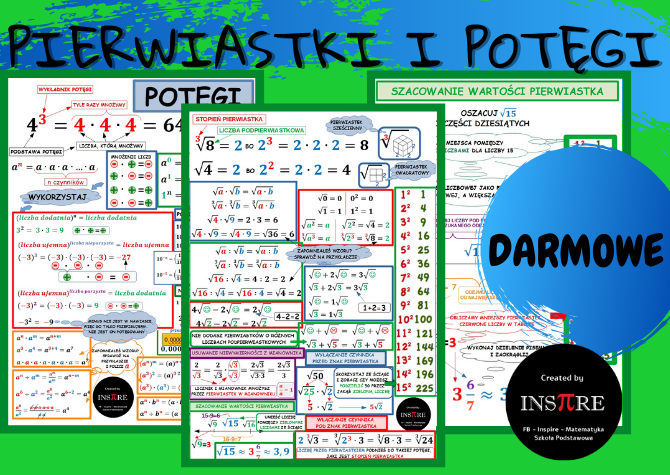
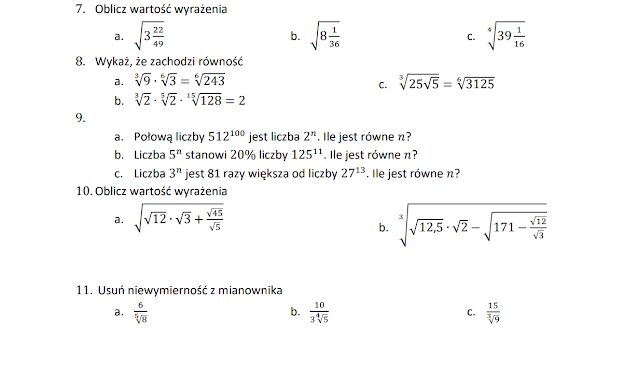Pierwiastki I Potęgi Klasa 8

Witaj w świecie pierwiastków i potęg! Ten artykuł jest skierowany do uczniów klasy 8 i ma na celu wyjaśnienie tych fundamentalnych pojęć matematycznych w sposób przystępny i zrozumiały. Zrozumienie pierwiastków i potęg jest kluczowe nie tylko do dalszej nauki matematyki, ale także do rozwiązywania problemów w życiu codziennym i różnych dziedzinach nauki.

Potęgi – co to takiego?

Potęga to nic innego jak skrócony zapis mnożenia tej samej liczby przez samą siebie. Zamiast pisać 2 * 2 * 2 * 2, możemy zapisać to jako 2⁴. Liczba 2 nazywana jest podstawą potęgi, a liczba 4 nazywana jest wykładnikiem potęgi. Wykładnik potęgi mówi nam, ile razy podstawa ma być przez siebie pomnożona.

Inaczej mówiąc, aⁿ = a * a * a * ... * a (n razy), gdzie 'a' jest podstawą, a 'n' jest wykładnikiem.

Podstawowe własności potęg

Z potęgami wiążą się pewne własności, które ułatwiają obliczenia:

Mnożenie potęg o tej samej podstawie: a^m * aⁿ = a^m+n (np. 2³ * 2² = 2³⁺² = 2⁵)
Dzielenie potęg o tej samej podstawie: a^m / aⁿ = a^m-n (np. 3⁵ / 3² = 3^5-2 = 3³)
Potęgowanie potęgi: (a^m)ⁿ = a^m*n (np. (5²)³ = 5^2*3 = 5⁶)
Potęgowanie iloczynu: (a * b)ⁿ = aⁿ * bⁿ (np. (2 * 3)² = 2² * 3² = 4 * 9 = 36)
Potęgowanie ilorazu: (a / b)ⁿ = aⁿ / bⁿ (np. (6 / 2)³ = 6³ / 2³ = 216 / 8 = 27)
a⁰ = 1 (dla a ≠ 0) – dowolna liczba (różna od zera) podniesiona do potęgi 0 daje 1 (np. 7⁰ = 1)
a¹ = a – dowolna liczba podniesiona do potęgi 1 daje samą siebie (np. 10¹ = 10)

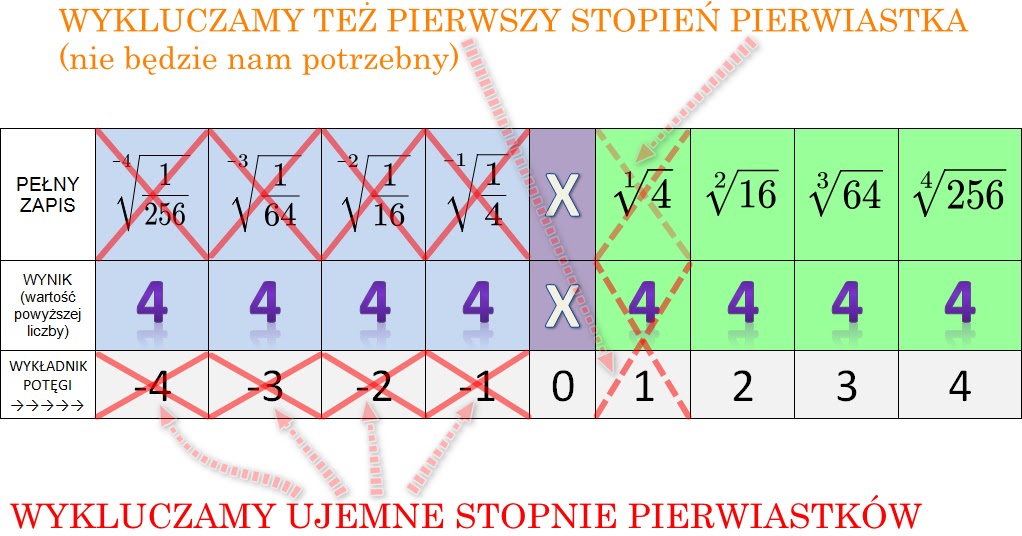
Potęgi o wykładniku ujemnym

Co się dzieje, gdy wykładnik jest ujemny? Potęga o wykładniku ujemnym oznacza odwrotność liczby podniesionej do potęgi o wykładniku dodatnim: a^-n = 1 / aⁿ. Przykładowo, 2^-3 = 1 / 2³ = 1 / 8.

Pierwiastki – odwrotność potęgowania

Pierwiastek jest operacją odwrotną do potęgowania. Pierwiastek kwadratowy z liczby 'a' to taka liczba 'b', która podniesiona do kwadratu daje 'a'. Zapisujemy to jako √a = b, jeśli b² = a. Przykładowo, √9 = 3, ponieważ 3² = 9.

Mówimy o pierwiastku kwadratowym (√), ale istnieją też pierwiastki wyższych stopni. Pierwiastek trzeciego stopnia (sześcienny) z liczby 'a' to taka liczba 'b', która podniesiona do trzeciej potęgi daje 'a'. Zapisujemy to jako ³√a = b, jeśli b³ = a. Przykładowo, ³√8 = 2, ponieważ 2³ = 8.

Własności pierwiastków

Podobnie jak potęgi, pierwiastki mają swoje własności:

Pierwiastek z iloczynu: √(a * b) = √a * √b (np. √(4 * 9) = √4 * √9 = 2 * 3 = 6) - to dotyczy tylko pierwiastków parzystego stopnia.
Pierwiastek z ilorazu: √(a / b) = √a / √b (np. √(16 / 4) = √16 / √4 = 4 / 2 = 2) - to dotyczy tylko pierwiastków parzystego stopnia.
(√a)² = a (np. (√5)² = 5)
ⁿ√aⁿ = a (np. ³√2³ = ³√8 = 2) – o ile a jest nieujemne dla pierwiastków parzystego stopnia.

Upraszczanie wyrażeń z pierwiastkami

Często można uprościć wyrażenia zawierające pierwiastki. Np. √12 możemy zapisać jako √(4 * 3) = √4 * √3 = 2√3. Wyciąganie czynnika przed pierwiastek jest częstym zabiegiem, który ułatwia dalsze obliczenia.

Pierwiastki i potęgi w życiu codziennym

Możemy myśleć, że potęgi i pierwiastki to tylko abstrakcyjne pojęcia matematyczne, ale mają one zastosowanie w wielu dziedzinach życia.

Informatyka: Potęgi dwójki (2ⁿ) są fundamentalne w informatyce. Ilość pamięci w komputerze, rozmiar plików, rozdzielczość ekranu – wszystko to jest często wyrażane za pomocą potęg dwójki. Przykładowo, 1 kilobajt (KB) to 2¹⁰ bajtów (1024 bajty).
Finanse: Procent składany to przykład wykorzystania potęg. Jeśli wpłacimy do banku kwotę P na n lat z oprocentowaniem r w skali roku, to po n latach będziemy mieli P * (1 + r)ⁿ.
Nauki przyrodnicze: Skala Richtera, używana do pomiaru siły trzęsień ziemi, jest skalą logarytmiczną. Każdy kolejny stopień w skali Richtera oznacza dziesięciokrotny wzrost amplitudy drgań i około 32-krotny wzrost uwolnionej energii (w przybliżeniu 10^1.5).
Geometria: Obliczanie pól i objętości figur geometrycznych często wymaga użycia potęg. Pole kwadratu o boku 'a' to a², a objętość sześcianu o boku 'a' to a³. Twierdzenie Pitagorasa, a² + b² = c², również opiera się na potęgach.
Dźwięk: Decybele (dB), jednostka miary natężenia dźwięku, są skalą logarytmiczną, a zatem wykorzystują potęgi.

Przykłady i zadania

Żeby lepiej zrozumieć potęgi i pierwiastki, warto rozwiązać kilka zadań. Oto kilka przykładów:

Oblicz: 2⁵, 3⁴, 5³, 10²
Uprość: √(25 * 16), √(81 / 9), √72
Oblicz: 4^-2, 8^-1
Rozwiąż równanie: x² = 36, x³ = 8
Uprość wyrażenie: (a³ * b²)² / (a² * b)
Oblicz objętość sześcianu o boku 5 cm.
W banku zdeponowano 1000 zł na 3 lata przy oprocentowaniu rocznym 5%. Ile będzie na koncie po 3 latach?

Pamiętaj, praktyka czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz potęgi i pierwiastki.

Podsumowanie

Potęgi i pierwiastki to ważne narzędzia matematyczne, które warto dobrze opanować. Zrozumienie ich własności i zastosowań otwiera drzwi do bardziej zaawansowanych zagadnień matematycznych i pozwala na rozwiązywanie problemów w różnych dziedzinach życia. Nie bój się zadawać pytań i ćwicz regularnie, a potęgi i pierwiastki staną się Twoimi przyjaciółmi! Skorzystaj z dostępnych zasobów online, podręczników i pomocy nauczyciela, aby jeszcze lepiej zgłębić ten temat. Pamiętaj, że regularna nauka i rozwiązywanie zadań to klucz do sukcesu!

Powodzenia!