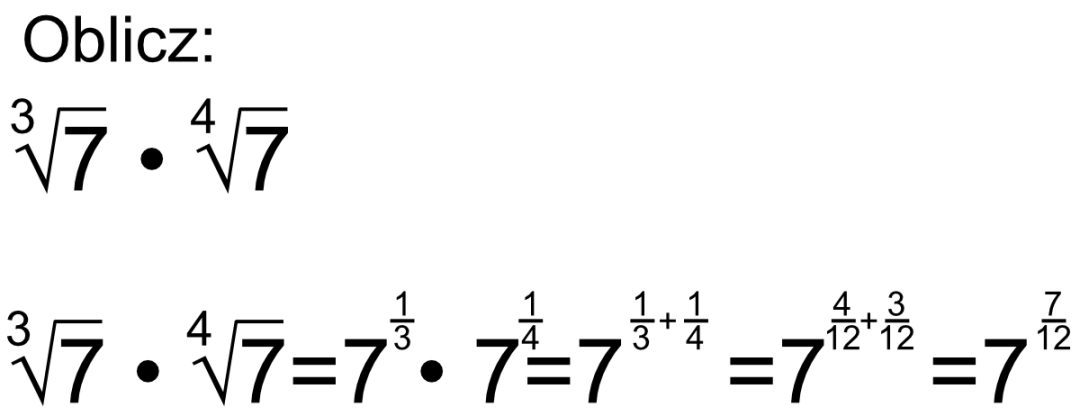Pierwiastki I Potęgi Klasa 7 Sprawdzian

Czy czeka Cię sprawdzian z pierwiastków i potęg w klasie 7? Nie martw się! Ten artykuł jest Twoim kompleksowym przewodnikiem, który pomoże Ci zrozumieć te zagadnienia, opanować niezbędne umiejętności i pewnie podejść do egzaminu.

Niezależnie od tego, czy czujesz się pewnie w matematyce, czy potrzebujesz dodatkowego wsparcia, znajdziesz tutaj jasne wyjaśnienia, przykłady i praktyczne wskazówki. Naszym celem jest przekształcenie trudnych koncepcji w proste i zrozumiałe informacje.

Dlaczego Pierwiastki i Potęgi Są Ważne?

Potęgi i pierwiastki to fundament matematyki, który wykorzystywany jest w wielu dziedzinach nauki i życia codziennego. Zrozumienie ich zasad jest kluczowe do dalszego rozwoju umiejętności matematycznych.

Oto dlaczego warto poświęcić im czas i energię:

Podstawa dalszej nauki: Bez solidnych podstaw z potęg i pierwiastków, dalsze zagadnienia matematyczne, takie jak algebra, geometria, czy funkcja, mogą sprawiać trudności.
Praktyczne zastosowania: Potęgi i pierwiastki są wykorzystywane w informatyce (np. przy określaniu złożoności algorytmów), fizyce (np. przy obliczeniach związanych z energią kinetyczną), ekonomii (np. przy obliczaniu procentu składanego) i wielu innych dziedzinach.
Rozwój logicznego myślenia: Praca z potęgami i pierwiastkami rozwija umiejętność logicznego myślenia, analizowania i rozwiązywania problemów, co przydaje się w wielu aspektach życia.

Potęgi - Wprowadzenie i Podstawowe Zasady

Co to jest potęga?

Potęga to skrócony zapis mnożenia tego samego czynnika przez siebie wiele razy. Na przykład, 2³ oznacza 2 * 2 * 2.

W zapisie aⁿ:

a to podstawa potęgi
n to wykładnik potęgi

Mówimy: "a do potęgi n" lub "a podniesione do potęgi n".

Podstawowe zasady działań na potęgach:

"Zapamiętaj te zasady! Są niezbędne do rozwiązywania zadań."

Mnożenie potęg o tej samej podstawie: a^m * aⁿ = a^m+n
Przykład: 2³ * 2² = 2³⁺² = 2⁵ = 32
Dzielenie potęg o tej samej podstawie: a^m / aⁿ = a^m-n (dla a ≠ 0)
Przykład: 3⁵ / 3² = 3^5-2 = 3³ = 27
Potęgowanie potęgi: (a^m)ⁿ = a^m*n
Przykład: (5²)³ = 5^2*3 = 5⁶ = 15625
Potęgowanie iloczynu: (a * b)ⁿ = aⁿ * bⁿ
Przykład: (2 * 3)² = 2² * 3² = 4 * 9 = 36
Potęgowanie ilorazu: (a / b)ⁿ = aⁿ / bⁿ (dla b ≠ 0)
Przykład: (6 / 2)³ = 6³ / 2³ = 216 / 8 = 27
Potęga o wykładniku zero: a⁰ = 1 (dla a ≠ 0)
Przykład: 7⁰ = 1
Potęga o wykładniku jeden: a¹ = a
Przykład: 10¹ = 10
Potęgi o wykładniku ujemnym: a^-n = 1 / aⁿ (dla a ≠ 0)
Przykład: 2^-3 = 1 / 2³ = 1 / 8

Przykładowe zadania z potęgami:

Uprość wyrażenie: (x⁴ * x²) / x³
Rozwiązanie: (x⁴ * x²) / x³ = x⁴⁺² / x³ = x⁶ / x³ = x^6-3 = x³
Oblicz: (3²)² * 3^-1
Rozwiązanie: (3²)² * 3^-1 = 3^2*2 * 3^-1 = 3⁴ * 3^-1 = 3^4-1 = 3³ = 27

Pierwiastki - Wprowadzenie i Podstawowe Zasady

Co to jest pierwiastek?

Pierwiastek to działanie odwrotne do potęgowania. Pierwiastek n-tego stopnia z liczby a, oznaczany jako ⁿ√a, to taka liczba b, że bⁿ = a.

W zapisie ⁿ√a:

n to stopień pierwiastka (jeśli n = 2, to pierwiastek kwadratowy; jeśli n = 3, to pierwiastek sześcienny)
a to liczba podpierwiastkowa

Mówimy: "pierwiastek n-tego stopnia z a".

Podstawowe zasady działań na pierwiastkach:

Pierwiastek z iloczynu: ⁿ√(a * b) = ⁿ√a * ⁿ√b (dla a ≥ 0 i b ≥ 0, jeśli n jest parzyste)
Przykład: √ (4 * 9) = √4 * √9 = 2 * 3 = 6
Pierwiastek z ilorazu: ⁿ√(a / b) = ⁿ√a / ⁿ√b (dla a ≥ 0 i b > 0, jeśli n jest parzyste)
Przykład: √(16 / 4) = √16 / √4 = 4 / 2 = 2
Potęgowanie pierwiastka: (ⁿ√a)^m = ⁿ√(a^m) (dla a ≥ 0, jeśli n jest parzyste)
Przykład: (√4)³ = √(4³) = √64 = 8

Upraszczanie wyrażeń z pierwiastkami:

Często możemy uprościć wyrażenia z pierwiastkami, wyłączając czynnik przed znak pierwiastka.

Przykład: √12 = √(4 * 3) = √4 * √3 = 2√3

Usuwanie niewymierności z mianownika:

Jeśli w mianowniku ułamka występuje pierwiastek, możemy go usunąć, mnożąc licznik i mianownik przez odpowiedni czynnik.

Przykład: 1 / √2 = (1 * √2) / (√2 * √2) = √2 / 2

Przykładowe zadania z pierwiastkami:

Oblicz: √(25 + 144)
Rozwiązanie: √(25 + 144) = √169 = 13
Uprość wyrażenie: √18 + √32 - √50
Rozwiązanie: √18 + √32 - √50 = √(9 * 2) + √(16 * 2) - √(25 * 2) = 3√2 + 4√2 - 5√2 = (3 + 4 - 5)√2 = 2√2
Usuń niewymierność z mianownika: 3 / √3
Rozwiązanie: 3 / √3 = (3 * √3) / (√3 * √3) = 3√3 / 3 = √3

Praktyczne Wskazówki na Sprawdzian

Oto kilka praktycznych wskazówek, które pomogą Ci przygotować się do sprawdzianu z potęg i pierwiastków:

Powtórz definicje i wzory: Upewnij się, że rozumiesz definicje potęg i pierwiastków oraz znasz wszystkie wzory.
Rozwiązuj zadania: Im więcej zadań rozwiążesz, tym lepiej utrwalisz wiedzę i nabierzesz wprawy. Korzystaj z podręcznika, zbiorów zadań i internetowych zasobów.
Analizuj błędy: Jeśli popełniasz błędy, dokładnie przeanalizuj, dlaczego tak się stało. Zrozumienie błędów jest kluczem do ich uniknięcia w przyszłości.
Poproś o pomoc: Jeśli masz trudności z jakimś zagadnieniem, nie wahaj się poprosić o pomoc nauczyciela, kolegę lub korepetytora.
Zadbaj o odpoczynek: Wyspany i wypoczęty umysł lepiej przyswaja wiedzę. Nie zostawiaj nauki na ostatnią chwilę.
Na sprawdzianie czytaj uważnie polecenia: Zanim zaczniesz rozwiązywać zadanie, upewnij się, że dobrze rozumiesz, co masz zrobić.
Sprawdzaj wyniki: Po rozwiązaniu zadania sprawdź, czy wynik jest logiczny i czy nie popełniłeś żadnych błędów rachunkowych.

Dodatkowe Zasoby

W Internecie znajdziesz wiele dodatkowych zasobów, które mogą pomóc Ci w nauce potęg i pierwiastków. Oto kilka propozycji:

Strony internetowe z materiałami edukacyjnymi: Khan Academy, Matematyka.pl
Filmy instruktażowe na YouTube: Szukaj filmów z przykładami rozwiązywania zadań i wyjaśnieniami teoretycznymi.
Aplikacje mobilne do nauki matematyki: PhotoMath, Symbolab

Podsumowanie

Opanowanie potęg i pierwiastków to ważny krok w rozwoju Twoich umiejętności matematycznych. Pamiętaj, że kluczem do sukcesu jest systematyczna praca, rozwiązywanie zadań i analizowanie błędów. Mamy nadzieję, że ten artykuł pomoże Ci przygotować się do sprawdzianu i osiągnąć sukces. Powodzenia!

Nie poddawaj się! Matematyka może być fascynująca i satysfakcjonująca, jeśli poświęcisz jej trochę czasu i uwagi.