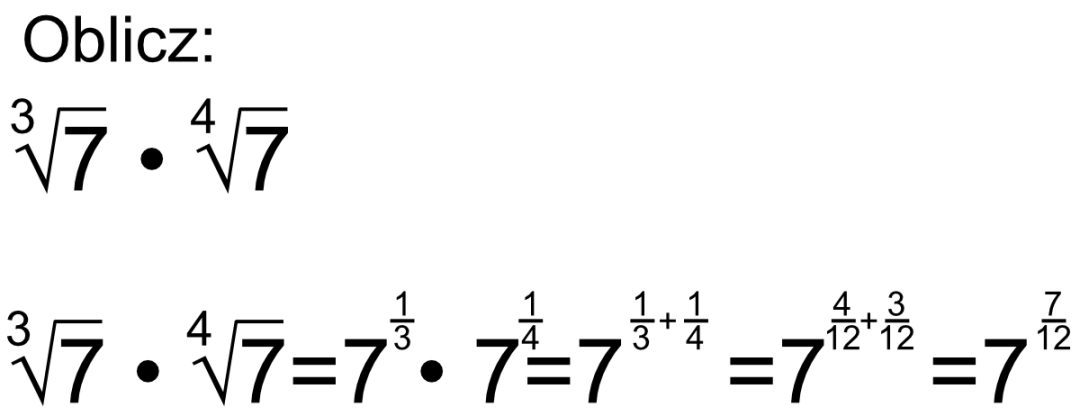Pierwiastki I Potęgi Klasa 7

Hej! Wiem, że pierwiastki i potęgi w klasie 7 mogą wydawać się trudne, jak zagadkowy labirynt pełen liczb i symboli. Ale spokojnie! Razem przejdziemy przez ten labirynt, odkryjemy wszystkie sekrety i sprawimy, że poczujesz się pewnie rozwiązując zadania.

Pamiętam swoje pierwsze spotkanie z potęgami – wydawało mi się to strasznie skomplikowane. Ale uwierz mi, po prostu potrzebujesz odpowiedniego przewodnika i kilku sprawdzonych trików. Zatem, zaczynamy?

Potęgi – co to właściwie jest?

Potęga to nic innego jak skrócony zapis mnożenia tej samej liczby przez siebie. Zamiast pisać 2 * 2 * 2 * 2 * 2, możemy zapisać to jako 2⁵. Ta mała 5 u góry, to wykładnik, a liczba 2 to podstawa potęgi. Wykładnik mówi nam, ile razy podstawa ma być przez siebie pomnożona.

Podstawowe zasady potęgowania:

aⁿ = a * a * a * ... * a (n razy)
a¹ = a (Każda liczba podniesiona do potęgi 1 równa się samej sobie.)
a⁰ = 1 (Każda liczba (oprócz 0) podniesiona do potęgi 0 równa się 1. Dlaczego? Bo to po prostu umowa matematyczna, która ułatwia nam życie!)

Spróbujmy z kilkoma przykładami:

3² = 3 * 3 = 9
5³ = 5 * 5 * 5 = 125
10⁴ = 10 * 10 * 10 * 10 = 10000

Widzisz? To wcale nie jest takie straszne! Najważniejsze to zapamiętać definicję i poćwiczyć na przykładach.

Działania na potęgach – triki, które ułatwią Ci życie!

Teraz, gdy już wiemy, czym są potęgi, pora na bardziej zaawansowane zagadnienia – działania na potęgach. Tu pojawiają się różne wzory, które na początku mogą wydawać się skomplikowane, ale spokojnie, rozłożymy je na czynniki pierwsze (pun intended! ;)).

Mnożenie potęg o tej samej podstawie:

Jeśli mamy dwie potęgi o tej samej podstawie, to przy mnożeniu dodajemy wykładniki.

a^m * aⁿ = a^m+n

Przykład:

2³ * 2² = 2³⁺² = 2⁵ = 32

Dzielenie potęg o tej samej podstawie:

Analogicznie, przy dzieleniu potęg o tej samej podstawie odejmujemy wykładniki.

a^m / aⁿ = a^m-n (gdzie a ≠ 0)

Przykład:

5⁵ / 5² = 5^5-2 = 5³ = 125

Potęgowanie potęgi:

Jeśli potęga jest podniesiona do innej potęgi, to mnożymy wykładniki.

(a^m)ⁿ = a^m*n

Przykład:

(3²)³ = 3^2*3 = 3⁶ = 729

Potęgowanie iloczynu i ilorazu:

Jeśli mamy iloczyn lub iloraz podniesiony do potęgi, to możemy podnieść każdy element osobno.

(a * b)ⁿ = aⁿ * bⁿ

(a / b)ⁿ = aⁿ / bⁿ (gdzie b ≠ 0)

Przykłady:

(2 * 3)² = 2² * 3² = 4 * 9 = 36
(10 / 2)³ = 10³ / 2³ = 1000 / 8 = 125

Pamiętaj, ćwiczenie czyni mistrza! Im więcej zadań rozwiążesz, tym bardziej te wzory wejdą Ci w krew.

Pierwiastki – odkrywamy tajemnice ukrytych liczb

Pierwiastek to operacja odwrotna do potęgowania. Pytamy: "Jaka liczba podniesiona do danej potęgi da nam liczbę pod pierwiastkiem?". Na przykład, pierwiastek kwadratowy z 9 to 3, bo 3 * 3 = 9.

Oznaczenie: √ (pierwiastek kwadratowy), ³√ (pierwiastek sześcienny), ⁿ√ (pierwiastek n-tego stopnia).

Podstawowe rodzaje pierwiastków:

Pierwiastek kwadratowy (√) – szukamy liczby, która pomnożona przez siebie da nam liczbę pod pierwiastkiem. np. √25 = 5, bo 5 * 5 = 25
Pierwiastek sześcienny (³√) – szukamy liczby, która pomnożona przez siebie trzy razy da nam liczbę pod pierwiastkiem. np. ³√8 = 2, bo 2 * 2 * 2 = 8

Jak znaleźć pierwiastek?

Dla małych liczb – możemy zgadywać! Sprawdź kilka liczb, aż trafisz na odpowiednią.
Dla większych liczb – często musimy poszukać czynników pierwszych liczby pod pierwiastkiem.

Przykład:

√36 = √ (2 * 2 * 3 * 3) = √ (2² * 3²) = 2 * 3 = 6

Działania na pierwiastkach – praktyczne wskazówki

Podobnie jak przy potęgach, możemy wykonywać działania na pierwiastkach. Ale uwaga, są pewne ograniczenia! Możemy mnożyć i dzielić pierwiastki tego samego stopnia.

Mnożenie pierwiastków:

ⁿ√a * ⁿ√b = ⁿ√(a * b)

Przykład:

√4 * √9 = √(4 * 9) = √36 = 6

Dzielenie pierwiastków:

ⁿ√a / ⁿ√b = ⁿ√(a / b) (gdzie b ≠ 0)

Przykład:

√100 / √4 = √(100 / 4) = √25 = 5

Wyłączanie czynnika przed pierwiastek:

To bardzo przydatna umiejętność! Jeśli liczba pod pierwiastkiem ma czynnik, który jest kwadratem liczby całkowitej (dla pierwiastka kwadratowego), możemy go "wyciągnąć" przed pierwiastek.

Przykład:

√12 = √(4 * 3) = √4 * √3 = 2√3

Potęgi i pierwiastki – połączenie idealne

Potęgi i pierwiastki są ze sobą ściśle powiązane. Możemy nawet zapisać pierwiastek jako potęgę o wykładniku ułamkowym!

ⁿ√a = a^1/n

Przykład:

√4 = 4^1/2 = 2

To pozwala nam stosować wzory na potęgi do pierwiastków i odwrotnie. To bardzo przydatne przy rozwiązywaniu bardziej skomplikowanych zadań.

Najczęstsze błędy i jak ich unikać

Podczas rozwiązywania zadań z potęg i pierwiastków łatwo o pomyłki. Oto kilka najczęstszych błędów i sposoby, jak ich unikać:

Pomylenie mnożenia z dodawaniem wykładników – pamiętaj, dodajemy wykładniki tylko przy mnożeniu potęg o tej samej podstawie!
Błędne obliczanie pierwiastków – zawsze sprawdzaj wynik, podnosząc go do odpowiedniej potęgi.
Zapominanie o kolejności wykonywania działań – najpierw potęgowanie/pierwiastkowanie, potem mnożenie/dzielenie, na końcu dodawanie/odejmowanie.
Nieumiejętne wyłączanie czynnika przed pierwiastek - upewnij się, że wyciągasz największy możliwy kwadrat liczby, żeby uprościć wynik.

Praktyczne zastosowania potęg i pierwiastków

Może się wydawać, że potęgi i pierwiastki to tylko abstrakcyjne pojęcia matematyczne. Nic bardziej mylnego! Znajdują one zastosowanie w wielu dziedzinach życia, na przykład:

Informatyka – w programowaniu potęgi są używane do obliczania rozmiarów pamięci, złożoności algorytmów itp.
Fizyka – potęgi i pierwiastki są używane w obliczeniach związanych z ruchem, energią, siłą itp.
Finanse – obliczanie procentu składanego, wartości inwestycji w czasie.
Geometria – obliczanie pól i objętości figur geometrycznych.

Na przykład, jeśli chcesz obliczyć pole kwadratu o boku długości 5 cm, musisz podnieść 5 do potęgi 2 (5² = 25). Pole tego kwadratu to 25 cm².

Podsumowanie i dalsza nauka

Mam nadzieję, że ta podróż po świecie potęg i pierwiastków była dla Ciebie pouczająca i przyjemna. Pamiętaj, że kluczem do sukcesu jest praktyka! Rozwiązuj zadania, pytaj nauczyciela, szukaj odpowiedzi w Internecie. Im więcej będziesz ćwiczyć, tym bardziej poczujesz się pewnie i komfortowo z tymi zagadnieniami.

Dodatkowe źródła wiedzy: