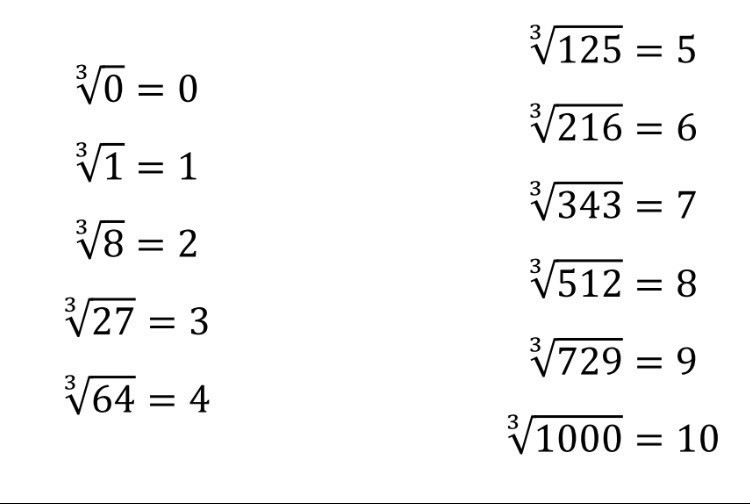Pierwiastek Trzeciego Stopnia Z 64

Rozważmy zagadnienie pierwiastka trzeciego stopnia z liczby 64. Jest to pojęcie fundamentalne w matematyce, które choć na pierwszy rzut oka wydaje się proste, kryje w sobie głębsze implikacje i zastosowania. W tym artykule dokładnie przeanalizujemy ten pierwiastek, wyjaśniając jego definicję, sposób obliczania, a także jego znaczenie w kontekście rzeczywistych problemów.

Definicja i Interpretacja Pierwiastka Trzeciego Stopnia

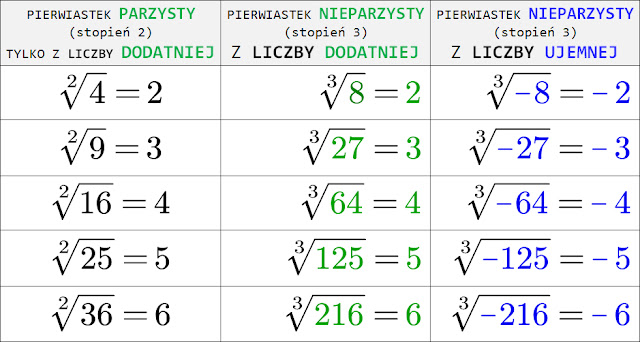
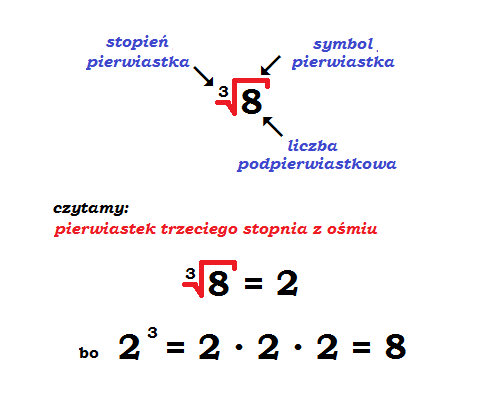
Pierwiastek trzeciego stopnia, zwany również pierwiastkiem sześciennym, z danej liczby x to taka liczba y, która podniesiona do potęgi trzeciej daje x. Matematycznie zapisujemy to jako:

³√x = y ⇔ y³ = x

Oznacza to, że szukamy takiej liczby, którą musimy pomnożyć przez nią samą dwukrotnie, aby otrzymać liczbę, z której wyciągamy pierwiastek. W naszym przypadku, chcemy znaleźć taką liczbę y, że y³ = 64.

Wyjaśnienie na Przykładzie 64

Zatem, pierwiastek trzeciego stopnia z 64 to liczba, którą pomnożona przez siebie trzykrotnie da nam 64. Aby to znaleźć, możemy posłużyć się różnymi metodami, ale w tym przypadku, najprościej jest po prostu spróbować kilku liczb. Wiemy, że 2³ = 8 i 3³ = 27. Spróbujmy 4: 4³ = 4 * 4 * 4 = 16 * 4 = 64. Zatem:

³√64 = 4

Oznacza to, że 4 podniesione do potęgi trzeciej daje nam 64. To bardzo proste, ale kluczowe zrozumienie definicji pierwiastka sześciennego.

Metody Obliczania Pierwiastka Trzeciego Stopnia

Chociaż dla małych liczb, takich jak 64, obliczenie pierwiastka trzeciego stopnia jest proste, dla większych i bardziej skomplikowanych liczb sytuacja się komplikuje. Istnieją różne metody obliczania pierwiastków trzeciego stopnia, zarówno ręczne, jak i z wykorzystaniem narzędzi komputerowych.

Metoda Prób i Błędów

Jak widzieliśmy wcześniej, dla prostych liczb można stosować metodę prób i błędów. Polega ona na tym, że wybieramy kolejne liczby i sprawdzamy, czy ich trzecia potęga jest bliska liczbie, z której chcemy wyciągnąć pierwiastek. Jest to metoda czasochłonna i mało efektywna dla dużych liczb.

Faktoryzacja

Kolejną metodą jest faktoryzacja liczby na czynniki pierwsze. Jeśli uda nam się rozłożyć liczbę na czynniki pierwsze tak, że wystąpią one w grupach po trzy, to możemy łatwo wyciągnąć pierwiastek trzeciego stopnia. Na przykład, dla 64: 64 = 2 * 2 * 2 * 2 * 2 * 2 = (2 * 2) * (2 * 2) * (2 * 2) = 4 * 4 * 4. Zatem ³√64 = 4.

Użycie Kalkulatora lub Komputera

Najbardziej efektywną metodą dla bardziej skomplikowanych liczb jest użycie kalkulatora naukowego lub programu komputerowego. Większość kalkulatorów posiada funkcję obliczania pierwiastka dowolnego stopnia. W przypadku programów komputerowych, takich jak Excel, Python czy Matlab, istnieją wbudowane funkcje lub biblioteki, które umożliwiają szybkie i precyzyjne obliczenie pierwiastka trzeciego stopnia.

Przybliżenia Numeryczne

W niektórych przypadkach, gdy nie potrzebujemy bardzo dokładnej wartości pierwiastka, możemy skorzystać z przybliżeń numerycznych. Istnieją różne algorytmy, takie jak metoda Newtona-Raphsona, które pozwalają na iteracyjne obliczanie przybliżonej wartości pierwiastka z zadaną dokładnością. Choć metody te są bardziej złożone, mogą być przydatne w sytuacjach, gdy nie mamy dostępu do kalkulatora lub komputera.

Zastosowania Pierwiastka Trzeciego Stopnia w Praktyce

Pierwiastek trzeciego stopnia znajduje zastosowanie w wielu dziedzinach nauki i techniki. Jego znajomość jest niezbędna w rozwiązywaniu problemów związanych z geometrią, fizyką, inżynierią, a nawet w niektórych dziedzinach ekonomii.

Geometria

W geometrii, pierwiastek trzeciego stopnia pojawia się przy obliczaniu długości krawędzi sześcianu, znając jego objętość. Jeśli objętość sześcianu wynosi 64 cm³, to długość jego krawędzi wynosi ³√64 = 4 cm. Podobnie, przy obliczaniu wymiarów innych brył, takich jak kule czy stożki, pierwiastek trzeciego stopnia może być niezbędny.

Fizyka

W fizyce, pierwiastek trzeciego stopnia może pojawiać się w różnych kontekstach, na przykład przy analizie ruchu harmonicznego tłumionego, przy obliczaniu objętości cieczy czy gazów, czy też w termodynamice. Również w mechanice płynów znajdziemy przykłady zastosowania pierwiastka trzeciego stopnia przy analizie przepływów i obliczaniu prędkości.

Inżynieria

W inżynierii, pierwiastek trzeciego stopnia jest wykorzystywany w wielu obliczeniach związanych z projektowaniem konstrukcji, obliczaniem wytrzymałości materiałów, a także w inżynierii chemicznej przy analizie procesów technologicznych. Na przykład, przy projektowaniu zbiorników cylindrycznych, znajomość pierwiastka trzeciego stopnia może być niezbędna do obliczenia optymalnych wymiarów zbiornika.

Ekonomia

Nawet w ekonomii, choć rzadziej, pierwiastek trzeciego stopnia może znaleźć zastosowanie przy analizie niektórych modeli ekonomicznych, na przykład przy obliczaniu wskaźników produktywności lub efektywności inwestycji. W szczególności, w modelach wzrostu gospodarczego, gdzie produkcja zależy od kapitału podniesionego do pewnej potęgi (np. 1/3), pierwiastek trzeciego stopnia pośrednio wpływa na wynik.

Praktyczny Przykład: Projektowanie Sześcianu o Danej Objętości

Załóżmy, że mamy za zadanie zaprojektować sześcian, który ma pomieścić dokładnie 64 litry płynu. Wiemy, że 1 litr to 1000 cm³, więc objętość sześcianu musi wynosić 64 * 1000 = 64000 cm³. Aby obliczyć długość krawędzi sześcianu, musimy wyciągnąć pierwiastek trzeciego stopnia z objętości:

a = ³√64000

Możemy to obliczyć, rozkładając liczbę 64000 na czynniki pierwsze: 64000 = 64 * 1000 = 4³ * 10³ = (4 * 10)³ = 40³. Zatem:

a = ³√64000 = 40 cm

Oznacza to, że każda krawędź sześcianu musi mieć długość 40 cm, aby jego objętość wynosiła 64 litry. Jest to prosty, ale ilustrujący przykład, jak pierwiastek trzeciego stopnia może być wykorzystany w praktycznych obliczeniach.

Podsumowanie

Pierwiastek trzeciego stopnia z 64, czyli 4, jest prostym, ale ważnym przykładem fundamentalnego pojęcia matematycznego. Zrozumienie definicji i metod obliczania pierwiastka trzeciego stopnia jest kluczowe w wielu dziedzinach nauki i techniki. Od geometrii i fizyki, po inżynierię i ekonomię, pierwiastek trzeciego stopnia znajduje zastosowanie w rozwiązywaniu różnorodnych problemów. Zachęcam do dalszego zgłębiania wiedzy na temat pierwiastków i innych operacji matematycznych, gdyż stanowią one podstawę naszego rozumienia świata.

Pamiętaj, że matematyka, choć czasem wydaje się abstrakcyjna, jest narzędziem, które pozwala nam modelować i analizować rzeczywistość. Ćwicz regularnie, a staniesz się mistrzem obliczeń!