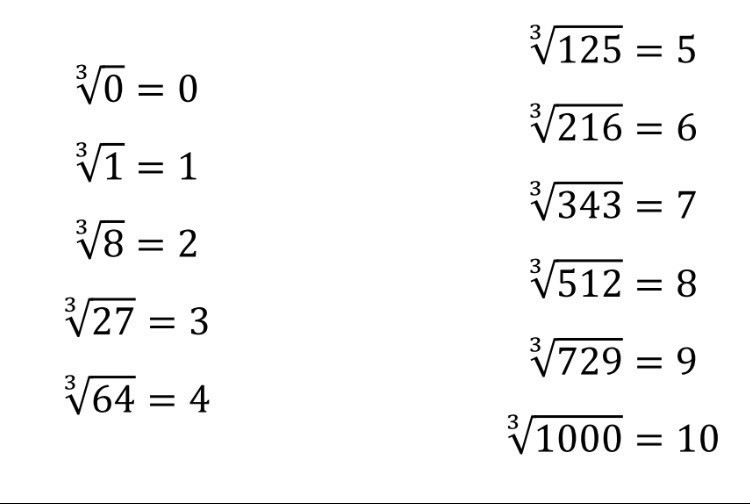Pierwiastek Trzeciego Stopnia Z 3

Czy zastanawiałeś się kiedyś nad liczbą, która ukrywa się w pozornie prostej operacji matematycznej – pierwiastkiem trzeciego stopnia z 3? To nie tylko abstrakcyjny koncept, ale liczba, która pojawia się w różnych dziedzinach, od geometrii po inżynierię. W tym artykule przyjrzymy się jej z bliska, zrozumieją jej właściwości i odkryjemy jej zastosowania. Artykuł ten skierowany jest do osób zainteresowanych matematyką, studentów, uczniów oraz każdego, kto chce poszerzyć swoją wiedzę o fascynującym świecie liczb.

Czym jest pierwiastek trzeciego stopnia?

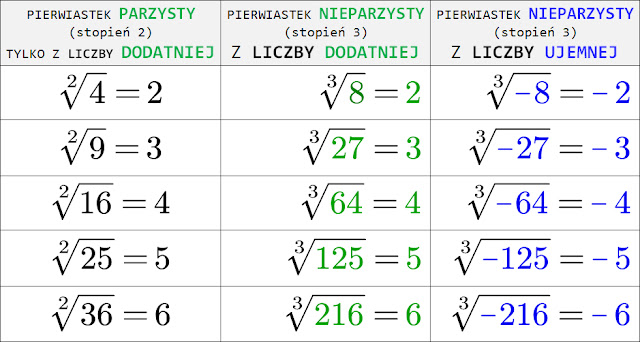
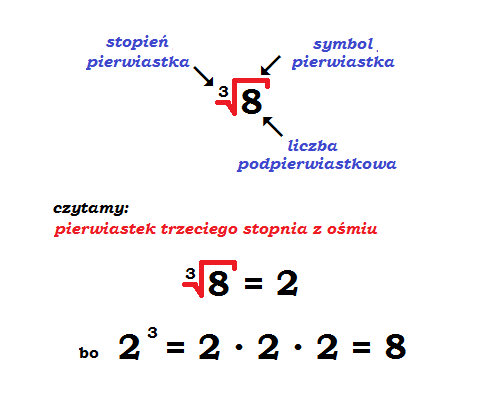
Zanim zagłębimy się w specyfikę pierwiastka trzeciego stopnia z 3, warto przypomnieć sobie podstawy. Pierwiastek trzeciego stopnia, inaczej pierwiastek sześcienny, to liczba, która pomnożona przez samą siebie trzykrotnie, daje liczbę, z której wyciągamy pierwiastek. Matematycznie zapisujemy to jako:

³√x = y, jeśli y * y * y = x.

Czyli, szukamy takiej liczby, którą podniesiona do potęgi trzeciej da nam x.

W naszym przypadku, x = 3. Zatem, pierwiastek trzeciego stopnia z 3 to liczba, która pomnożona przez samą siebie trzykrotnie daje 3.

Obliczanie pierwiastka trzeciego stopnia z 3

Obliczenie dokładnej wartości pierwiastka trzeciego stopnia z 3 bez użycia kalkulatora lub komputera jest trudne, ponieważ jest to liczba niewymierna. Oznacza to, że jej rozwinięcie dziesiętne jest nieskończone i nieokresowe. Jednak możemy przybliżyć jego wartość różnymi metodami:

• Użycie kalkulatora: Najprostszym sposobem jest użycie kalkulatora naukowego, który posiada funkcję obliczania pierwiastków dowolnego stopnia. Po prostu wpisujemy ³√3 i otrzymujemy przybliżoną wartość: 1.44224957...
• Metoda Newtona-Raphsona: Jest to metoda iteracyjna, która pozwala na przybliżanie wartości pierwiastków dowolnej funkcji. W przypadku pierwiastka trzeciego stopnia z 3, możemy zastosować wzór: x_n+1 = (2x_n + 3/x_n²) / 3. Zaczynamy od jakiegoś przybliżenia początkowego (np. x₀ = 1) i iteracyjnie obliczamy kolejne wartości x_n+1, które będą coraz bliższe prawdziwej wartości pierwiastka.
• Tablice matematyczne: W przeszłości, gdy kalkulatory nie były powszechne, używano tablic matematycznych, które zawierały przybliżone wartości pierwiastków dla różnych liczb.

Otrzymujemy więc, że ³√3 ≈ 1.44224957...

Właściwości pierwiastka trzeciego stopnia z 3

Pierwiastek trzeciego stopnia z 3 posiada kilka interesujących właściwości:

• Liczba niewymierna: Jak już wspomniano, jest to liczba niewymierna, co oznacza, że nie można jej zapisać jako ułamka dwóch liczb całkowitych.
• Liczba algebraiczna: Jest to liczba algebraiczna stopnia 3, ponieważ jest pierwiastkiem wielomianu x³ - 3 = 0.
• Należy do liczb rzeczywistych: Chociaż jest niewymierna, nadal jest liczbą rzeczywistą, co oznacza, że można ją przedstawić na osi liczbowej.

Zastosowania pierwiastka trzeciego stopnia z 3

Chociaż może się wydawać, że pierwiastek trzeciego stopnia z 3 to jedynie abstrakcyjna liczba, znajduje ona zastosowanie w różnych dziedzinach nauki i techniki:

Geometria

W geometrii pierwiastek trzeciego stopnia z 3 może pojawić się w obliczeniach związanych z objętością brył. Na przykład, jeśli mamy sześcian o objętości 3, to długość jego krawędzi wynosi właśnie ³√3.

Inżynieria

W inżynierii, szczególnie w obliczeniach wytrzymałościowych, może pojawić się podczas analizy naprężeń i odkształceń w elementach konstrukcyjnych. Konkretnie, może być używany przy obliczeniach dotyczących materiałów izotropowych.

Fizyka

W fizyce, chociaż rzadziej niż inne pierwiastki, może pojawić się w niektórych modelach teoretycznych i obliczeniach, szczególnie związanych z mechaniką płynów lub termodynamiką.

Informatyka

W informatyce może być używany w algorytmach aproksymacyjnych lub w analizie złożoności obliczeniowej niektórych problemów. Można go spotkać w algorytmach kompresji danych.

Dlaczego warto wiedzieć o pierwiastku trzeciego stopnia z 3?

Zrozumienie, czym jest pierwiastek trzeciego stopnia z 3, nie tylko poszerza Twoją wiedzę matematyczną, ale również rozwija umiejętność logicznego myślenia i rozwiązywania problemów. Wiedza ta może być przydatna w różnych sytuacjach, zarówno w życiu codziennym, jak i w bardziej zaawansowanych studiach lub pracy zawodowej.

Dodatkowo, rozważanie takich liczb, jak pierwiastek trzeciego stopnia z 3, pozwala nam docenić piękno i złożoność matematyki. Pokazuje, że nawet pozornie proste operacje mogą prowadzić do fascynujących odkryć i zastosowań.

Pomyśl o tym, jak często używamy kalkulatorów i komputerów, nie zastanawiając się nad tym, co kryje się za wyświetlanymi wynikami. Zagłębienie się w temat pierwiastków, takich jak ten, pozwala nam zrozumieć mechanizmy obliczeniowe i docenić pracę matematyków, którzy przez wieki rozwijali tę dziedzinę nauki.

Wiedza o liczbach niewymiernych, takich jak pierwiastek trzeciego stopnia z 3, jest fundamentem dla zrozumienia bardziej zaawansowanych koncepcji matematycznych, takich jak analiza matematyczna, geometria różniczkowa czy teoria liczb. To inwestycja w Twoją matematyczną przyszłość!

Nie bójmy się więc liczb niewymiernych! Zamiast tego, spróbujmy je zrozumieć i docenić ich znaczenie w świecie matematyki i nauki. To one często kryją w sobie klucz do rozwiązywania trudnych problemów.

Podsumowanie

Pierwiastek trzeciego stopnia z 3 to liczba niewymierna, algebraiczna i rzeczywista, która znajduje zastosowanie w różnych dziedzinach, od geometrii po inżynierię. Choć może wydawać się abstrakcyjna, zrozumienie jej właściwości pozwala na poszerzenie wiedzy matematycznej i rozwój umiejętności logicznego myślenia. Mamy nadzieję, że ten artykuł przybliżył Ci tę fascynującą liczbę i zainspirował do dalszej eksploracji świata matematyki. Pamiętajmy, że matematyka to nie tylko zbiór wzorów, ale przede wszystkim sposób myślenia i rozumienia świata!