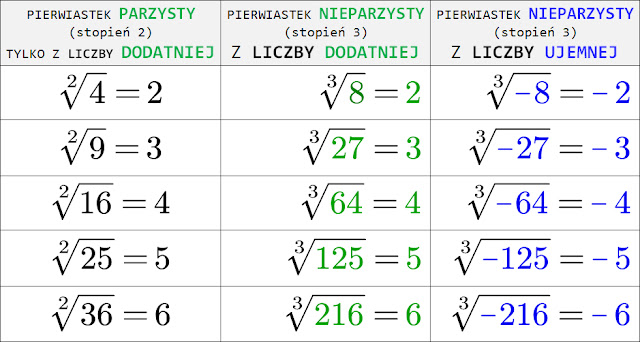
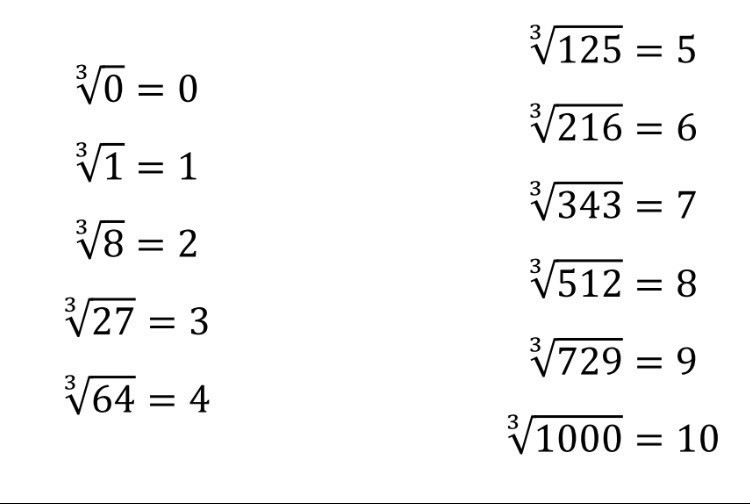Pierwiastek 3 Stopnia Z 3

W matematyce, pierwiastek trzeciego stopnia z liczby, czyli pierwiastek sześcienny, to taka liczba, która podniesiona do potęgi trzeciej daje liczbę wyjściową. Oznaczamy go symbolem ∛. W tym artykule zgłębimy temat pierwiastka trzeciego stopnia z 3 (∛3), analizując jego właściwości, metody obliczania i zastosowania.

Czym jest Pierwiastek Trzeciego Stopnia z 3?

Pierwiastek trzeciego stopnia z 3 to liczba, która pomnożona przez samą siebie trzykrotnie, daje w wyniku 3. Formalnie, jeśli x = ∛3, to x * x * x = 3. Jest to liczba niewymierna, co oznacza, że nie można jej wyrazić jako prostego ułamka zwykłego (a/b, gdzie a i b są liczbami całkowitymi, a b ≠ 0). Jej rozwinięcie dziesiętne jest nieskończone i nieokresowe. Przybliżona wartość ∛3 wynosi 1.44224957030740838232163831078010959276...

Niewymierność Pierwiastka Trzeciego Stopnia z 3

Warto podkreślić, że ∛3 jest liczbą algebraiczną, co oznacza, że jest pierwiastkiem pewnego wielomianu o współczynnikach całkowitych. W tym przypadku, jest pierwiastkiem wielomianu x³ - 3 = 0. Dowód niewymierności ∛3 można przeprowadzić podobnie jak dowód niewymierności pierwiastka kwadratowego z 2, stosując metodę sprowadzenia do sprzeczności. Zakładając, że ∛3 jest liczbą wymierną (a/b, gdzie a i b są względnie pierwsze), otrzymamy sprzeczność, co dowodzi, że ∛3 jest niewymierne.

Metody Obliczania Pierwiastka Trzeciego Stopnia z 3

Obliczanie pierwiastka trzeciego stopnia z 3 nie jest tak proste jak pierwiastka kwadratowego dla idealnych kwadratów. Istnieje kilka metod, które pozwalają na jego przybliżenie:

Metoda Newtona-Raphsona

Jest to iteracyjna metoda numeryczna, która pozwala na przybliżenie pierwiastka równania. Dla funkcji f(x) = x³ - 3, wzór iteracyjny wygląda następująco: x_n+1 = x_n - f(x_n)/f'(x_n). W tym przypadku f'(x) = 3x², więc wzór upraszcza się do: x_n+1 = x_n - (x_n³ - 3)/(3x_n²). Zaczynając od początkowego przybliżenia (np. x₀ = 1), kolejne iteracje dają coraz dokładniejsze wyniki. Ta metoda jest stosunkowo szybka i efektywna.

Szereg Taylora

Pierwiastek sześcienny z 3 można przybliżyć za pomocą szeregu Taylora dla funkcji (1+x)ⁿ w otoczeniu punktu x = 0. Ponieważ 3 = 27/9 = 27 * (1/9) = 27 * (1/8 + 1/72) = 27*(1/8)*(1+1/9), możemy skorzystać z tego faktu. Wzór ogólny dla (1+x)^1/3 to: 1 + (1/3)x - (1/9)x² + (5/81)x³ - .... Podstawiając x=1/9 i mnożąc przez pierwiastek sześcienny z 27/8 (czyli 3/2), uzyskujemy przybliżenie. Wraz ze wzrostem liczby członów szeregu, przybliżenie staje się dokładniejsze, jednak metoda ta może być wolniejsza od metody Newtona-Raphsona.

Kalkulatory i Programy Komputerowe

W praktyce, najprostszym sposobem na obliczenie pierwiastka trzeciego stopnia z 3 jest użycie kalkulatora naukowego lub programu komputerowego (np. Python, MATLAB, Mathematica). Te narzędzia wykorzystują zaawansowane algorytmy numeryczne do szybkiego i dokładnego obliczania wartości.

Właściwości Pierwiastka Trzeciego Stopnia z 3

Oprócz bycia liczbą niewymierną, ∛3 posiada kilka innych interesujących właściwości:

Liczba Algebraiczna

Jak wspomniano wcześniej, ∛3 jest liczbą algebraiczną stopnia 3, ponieważ jest pierwiastkiem wielomianu x³ - 3 = 0. To oznacza, że można go wyrazić za pomocą pierwiastków wielomianu o współczynnikach wymiernych.

Relacje z Innymi Liczbami Niewymiernymi

∛3 może występować w różnych wyrażeniach matematycznych w połączeniu z innymi liczbami niewymiernymi, tworząc bardziej złożone wyrażenia. Na przykład, ∛3 + √2 jest również liczbą niewymierną i algebraiczną.

Zastosowania Pierwiastka Trzeciego Stopnia z 3

Chociaż ∛3 sam w sobie nie pojawia się bezpośrednio w wielu praktycznych zastosowaniach w sposób tak oczywisty jak np. √2 (przekątna kwadratu), odgrywa rolę w różnych dziedzinach nauki i inżynierii:

Geometria i Objętość

Pierwiastki trzeciego stopnia pojawiają się w obliczeniach związanych z objętością. Na przykład, jeśli mamy sześcian o objętości 3 jednostki sześciennej, to długość jego boku wynosi ∛3. W bardziej złożonych kształtach, obliczenia objętości mogą również prowadzić do wyrażeń zawierających pierwiastki trzeciego stopnia.

Inżynieria

W niektórych dziedzinach inżynierii, takich jak mechanika płynów lub termodynamika, pewne równania mogą zawierać pierwiastki trzeciego stopnia w zależności od przyjętych uproszczeń i modelowania. Analiza numeryczna i symulacje komputerowe często wykorzystują przybliżenia numeryczne ∛3 do rozwiązywania takich problemów.

Matematyka Teoretyczna

Pierwiastki trzeciego stopnia odgrywają ważną rolę w teorii liczb i algebrze. Badanie własności pierwiastków równań wielomianowych, w tym tych stopnia 3, prowadzi do głębszego zrozumienia struktur algebraicznych. Znajomość ich własności jest kluczowa dla rozwiązywania równań.

Kryptografia

W niektórych systemach kryptograficznych, szczególnie tych opartych na krzywych eliptycznych, operacje z pierwiastkami modulo mogą być wykorzystywane. Choć ∛3 sam w sobie nie jest centralnym elementem, koncepcje związane z pierwiastkami modulo mają zastosowanie w zapewnieniu bezpieczeństwa danych.

Przykłady i Dane Rzeczywiste

Chociaż bezpośrednie przykłady użycia dokładnie ∛3 w życiu codziennym są rzadkie, koncepcja pierwiastków trzeciego stopnia jest powszechna. Rozważmy następujący scenariusz:

Problem: Projektant ma za zadanie stworzyć pojemnik w kształcie sześcianu, który pomieści dokładnie 3 litry płynu. Jaką długość boku powinien mieć ten pojemnik?

Rozwiązanie: 3 litry to 3000 cm³. Długość boku sześcianu (a) wynosi ∛3000 cm ≈ 14.42 cm. To pokazuje, jak pierwiastek trzeciego stopnia pojawia się w praktycznym problemie projektowym.

Innym przykładem może być obliczanie minimalnej wielkości ziarna kruszywa w betonach specjalnych, gdzie zależność pomiędzy wielkością ziaren a objętością porów powietrza może być wyrażona za pomocą funkcji zawierających pierwiastki sześcienne.

Podsumowanie

Pierwiastek trzeciego stopnia z 3 (∛3) jest liczbą niewymierną i algebraiczną, która odgrywa rolę w różnych dziedzinach matematyki, fizyki i inżynierii. Choć nie zawsze jest widoczny w codziennych zastosowaniach, koncepcja pierwiastków trzeciego stopnia jest niezbędna do rozwiązywania problemów związanych z objętością, modelowaniem matematycznym i innymi złożonymi zagadnieniami. Metody obliczania ∛3, takie jak metoda Newtona-Raphsona czy szereg Taylora, pokazują, jak można przybliżać wartości niewymierne za pomocą metod numerycznych. W dobie komputerów, obliczanie ∛3 jest proste i szybkie dzięki dostępnym narzędziom programistycznym i kalkulatorom.

Zrozumienie pierwiastka trzeciego stopnia z 3 pozwala na lepsze zrozumienie bardziej zaawansowanych koncepcji matematycznych i ich zastosowań w świecie rzeczywistym. Zachęcam do dalszego zgłębiania wiedzy z zakresu matematyki i jej zastosowań w innych dziedzinach!