Ostrosłup Prawidłowy Czworokątny Kąt Między ścianami Bocznymi

Dzień dobry wszystkim! Często dostaję pytania dotyczące ostrosłupów, a szczególnie tego prawidłowego czworokątnego i kąta między jego ścianami bocznymi. Spróbujmy to sobie wyjaśnić krok po kroku, tak żeby każdy zrozumiał.

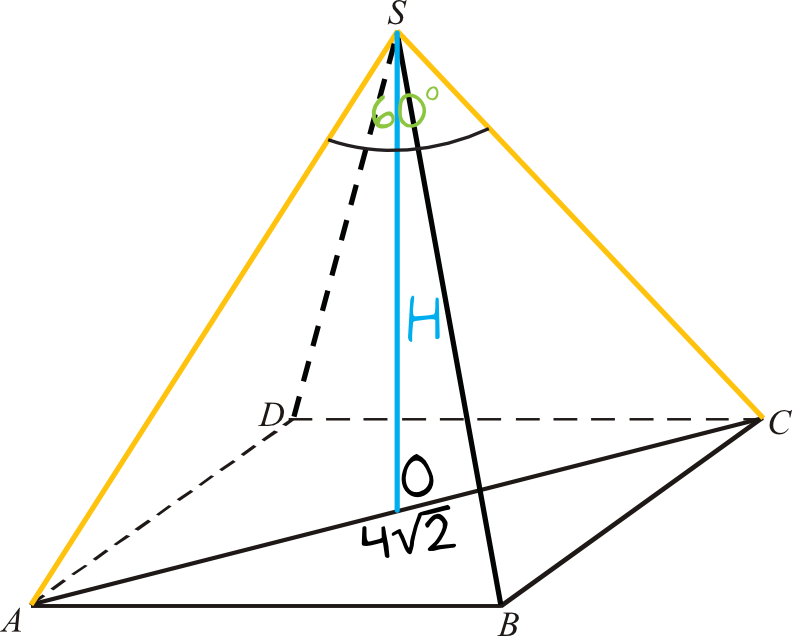
Zacznijmy od podstaw. Co to w ogóle jest ostrosłup prawidłowy czworokątny? Wyobraź sobie piramidę, ale taką bardzo regularną. "Prawidłowy" znaczy, że w podstawie mamy figurę foremną – w naszym przypadku kwadrat. "Czworokątny" informuje nas, że podstawa to czworokąt, czyli właśnie kwadrat. I na koniec "ostrosłup" – wszystkie wierzchołki tego kwadratu są połączone z jednym punktem leżącym ponad nim, tworząc ściany boczne, które są trójkątami równoramiennymi. Ten punkt, w którym schodzą się te trójkąty, nazywamy wierzchołkiem ostrosłupa.

Teraz przejdźmy do sedna – kąt między ścianami bocznymi. To trochę bardziej skomplikowane, ale bez obaw, damy radę! Musimy sobie wyobrazić, gdzie ten kąt właściwie jest. Otóż, jest to kąt dwuścienny. Znajduje się on pomiędzy dwiema sąsiednimi ścianami bocznymi. Żeby go znaleźć, musimy poprowadzić proste prostopadłe do krawędzi bocznej, wzdłuż której stykają się te ściany. Punkt, w którym te proste się przecinają (na tej krawędzi bocznej), jest wierzchołkiem naszego kąta dwuściennego. Ramiona tego kąta leżą na ścianach bocznych i są prostopadłe do krawędzi bocznej.

Jak to policzyć? To zależy od tego, co wiemy o ostrosłupie. Najczęściej będziemy potrzebować albo długości krawędzi podstawy (oznaczmy ją jako 'a'), albo wysokości ostrosłupa (oznaczmy ją jako 'H'), albo wysokości ściany bocznej (oznaczmy ją jako 'h'). Czasami będziemy mieli dany kąt nachylenia ściany bocznej do podstawy (oznaczmy go jako 'α').

Wykorzystamy tutaj trochę trygonometrii i geometrii przestrzennej. Najpierw musimy znaleźć trójkąt, w którym znajduje się nasz kąt dwuścienny. Pomyślmy... Możemy sobie wyobrazić, że prowadzimy wysokość z wierzchołka ostrosłupa na podstawę. Potem łączymy spodek tej wysokości ze środkiem krawędzi podstawy. Powstaje nam trójkąt prostokątny. Następnie rysujemy wysokość ściany bocznej. Teraz mamy już kilka trójkątów prostokątnych, które możemy wykorzystać.

Obliczanie Kąta

Najczęściej korzysta się z twierdzenia cosinusów lub sinusów w trójkącie, którego wierzchołkami są spodki wysokości ścian bocznych opuszczonych na wspólną krawędź boczną i wierzchołek podstawy. Spróbujmy to rozpisać na przykładzie.

Załóżmy, że mamy ostrosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 'a', a wysokość ostrosłupa to 'H'. Chcemy obliczyć kąt 'β' między sąsiednimi ścianami bocznymi.

1. Znajdujemy wysokość ściany bocznej (h): Możemy to zrobić z twierdzenia Pitagorasa. Wiemy, że połowa krawędzi podstawy (a/2) i wysokość ostrosłupa (H) tworzą przyprostokątne trójkąta prostokątnego, a wysokość ściany bocznej (h) jest jego przeciwprostokątną. Czyli: h² = (a/2)² + H² => h = √( (a/2)² + H² ).

2. Obliczamy długość krawędzi bocznej (b): Znowu twierdzenie Pitagorasa! Tym razem patrzymy na trójkąt utworzony przez połowę przekątnej podstawy, wysokość ostrosłupa i krawędź boczną. Długość przekątnej podstawy to a√2, więc połowa to (a√2)/2. Zatem: b² = H² + ((a√2)/2)² => b = √(H² + (a²/2)).

3. Korzystamy z Twierdzenia Cosinusów: Teraz wyobraźmy sobie czworokąt, którego wierzchołkami są: wierzchołek ostrosłupa (W), środki dwóch sąsiednich krawędzi podstawy (S1 i S2) i wierzchołek podstawy (A) wspólny dla tych krawędzi. Długość odcinka WS1 i WS2 to wysokość ściany bocznej (h), długość odcinka AS1 i AS2 to połowa długości krawędzi podstawy (a/2) a długość odcinka WA to krawędź boczna ostrosłupa (b). Patrzymy na trójkąt S1AS2, gdzie odcinek S1S2 to długość krawędzi podstawy a. Wykorzystujemy twierdzenie cosinusów w trójkącie S1WS2, gdzie kąt S1WS2 to szukany kąt β: a² = h² + h² - 2 * h * h * cos(β). Przekształcamy wzór, aby wyznaczyć cos(β): cos(β) = (2h² - a²) / (2h²). Podstawiamy wyliczone wcześniej 'h' i 'a' i obliczamy wartość cos(β). Na koniec, żeby obliczyć sam kąt β, musimy użyć funkcji arcus cosinus (arccos) na kalkulatorze: β = arccos( (2h² - a²) / (2h²) ).

Pamiętajmy, że to tylko jeden przykład, a w zależności od tego, co mamy dane w zadaniu, będziemy musieli użyć innych zależności i wzorów. Kluczem jest zrozumienie geometrii ostrosłupa i umiejętność dostrzegania trójkątów prostokątnych, w których możemy wykorzystać twierdzenie Pitagorasa i funkcje trygonometryczne.

Inne Sposoby

Można też podejść do tego inaczej, jeśli znamy kąt nachylenia ściany bocznej do podstawy (α). Wtedy możemy zbudować trójkąt prostokątny, którego przyprostokątną jest wysokość ostrosłupa (H), a przeciwprostokątną jest wysokość ściany bocznej (h). Możemy wtedy wyrazić 'h' za pomocą 'H' i kąta 'α': h = H / sin(α). Następnie możemy wykorzystać to do obliczenia kąta β między ścianami bocznymi, jak opisałem wcześniej.

Ważne jest, żeby dobrze narysować sobie rysunek pomocniczy. Zaznacz na nim wszystkie dane, które masz podane w zadaniu, oraz oznacz kąt, który chcesz obliczyć. To bardzo ułatwia rozwiązanie zadania.

Podsumowując, obliczanie kąta między ścianami bocznymi ostrosłupa prawidłowego czworokątnego wymaga trochę wyobraźni przestrzennej i znajomości trygonometrii. Najważniejsze to:

1. Zrozumieć, co to jest ostrosłup prawidłowy czworokątny.
2. Zlokalizować kąt między ścianami bocznymi.
3. Wykorzystać twierdzenie Pitagorasa i funkcje trygonometryczne do obliczenia potrzebnych długości i kątów.
4. Zrobić dobry rysunek pomocniczy.

Mam nadzieję, że to wyjaśnienie było pomocne! Jeśli macie jeszcze jakieś pytania, śmiało pytajcie! Powodzenia w rozwiązywaniu zadań z ostrosłupami!