Osią Symetrii Wykresu Funkcji F Jest Prosta O Równaniu

Artykuł musi być napisany językiem formalnym.

Osią symetrii wykresu funkcji f jest prosta o równaniu... Ta krótka fraza otwiera drzwi do głębszego zrozumienia własności funkcji i ich wizualnej reprezentacji. Skupmy się na tym, co to właściwie oznacza i jak możemy to wykorzystać w analizie matematycznej.

Zanim jednak przejdziemy do konkretnych przykładów i metod identyfikacji osi symetrii, warto ustalić pewne fundamentalne pojęcia. Wyobraźmy sobie wykres funkcji narysowany na kartce papieru. Oś symetrii to prosta, wzdłuż której możemy złożyć tę kartkę tak, że obie połówki wykresu idealnie się pokrywają. Innymi słowy, dla każdego punktu na wykresie po jednej stronie osi, istnieje odpowiadający mu punkt po drugiej stronie, znajdujący się w tej samej odległości od osi.

Rozważmy funkcję kwadratową, na przykład f(x) = x². Jej wykres to parabola. Intuicyjnie czujemy, że parabola posiada oś symetrii. W tym przypadku, osią symetrii jest prosta o równaniu x = 0, czyli oś Y. Dlaczego tak jest? Spójrzmy na dowolny punkt na wykresie, na przykład (2, 4). Punkt symetryczny do niego względem osi Y to (-2, 4). Zauważmy, że oba punkty mają tę samą wartość y, a ich współrzędne x są liczbami przeciwnymi. Możemy to uogólnić: dla każdego x, f(x) = f(-x). To właśnie definiuje parzystość funkcji, a funkcje parzyste zawsze mają oś symetrii w postaci osi Y.

Ale co, jeśli funkcja nie jest tak prosta jak x²? Co, jeśli mamy bardziej złożoną funkcję kwadratową, na przykład f(x) = (x - 3)² + 2? Wykres tej funkcji to również parabola, ale przesunięta o 3 jednostki w prawo i 2 jednostki w górę. Intuicja podpowiada, że oś symetrii również się przesunęła. W tym przypadku, osią symetrii jest prosta o równaniu x = 3. Dlaczego? Zauważmy, że w punkcie x = 3 funkcja osiąga swoje minimum. Parabola jest symetryczna względem tego punktu. Możemy to zweryfikować, obliczając wartość funkcji dla x = 3 + a oraz x = 3 - a, gdzie a jest dowolną liczbą. Okazuje się, że f(3 + a) = f(3 - a) dla każdego a.

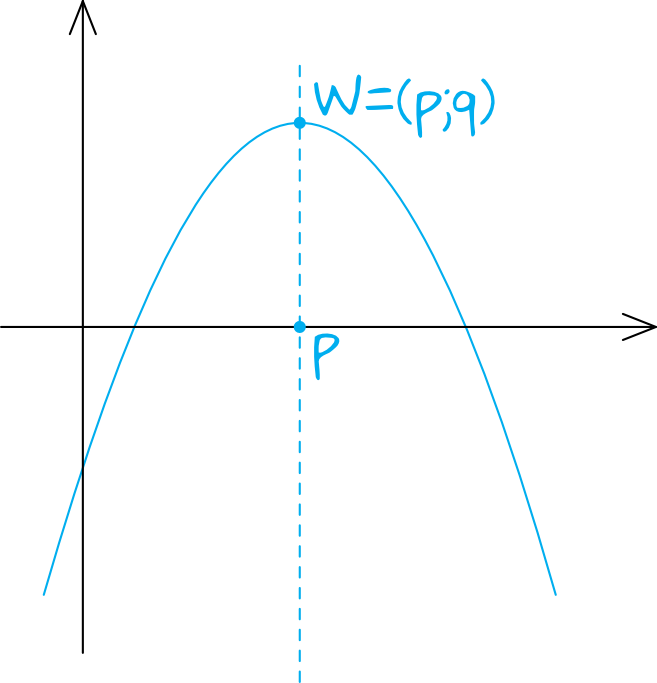
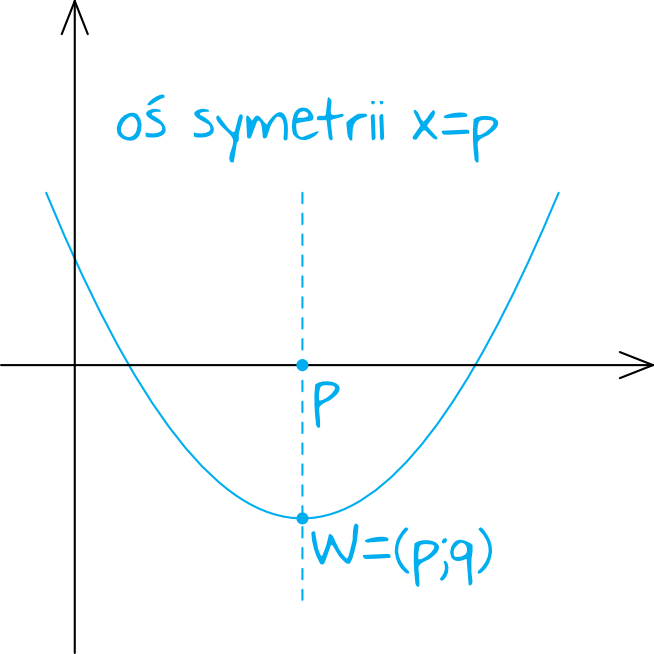
W ogólności, dla funkcji kwadratowej w postaci kanonicznej f(x) = a(x - p)² + q, osią symetrii jest prosta o równaniu x = p. Współczynnik 'a' determinuje kierunek otwarcia paraboli (w górę, jeśli a > 0, w dół, jeśli a < 0) oraz jej "szerokość", ale nie wpływa na położenie osi symetrii.

Znajdowanie Osi Symetrii

Jak zatem znaleźć oś symetrii, jeśli nie mamy postaci kanonicznej funkcji kwadratowej? Rozważmy funkcję kwadratową w postaci ogólnej f(x) = ax² + bx + c. Wiemy, że wierzchołek paraboli leży na osi symetrii. Współrzędna x wierzchołka paraboli dana jest wzorem x = -b / 2a. Zatem, osią symetrii jest prosta o równaniu x = -b / 2a. To bardzo użyteczny wzór, który pozwala nam szybko zidentyfikować oś symetrii dowolnej funkcji kwadratowej zapisanej w postaci ogólnej.

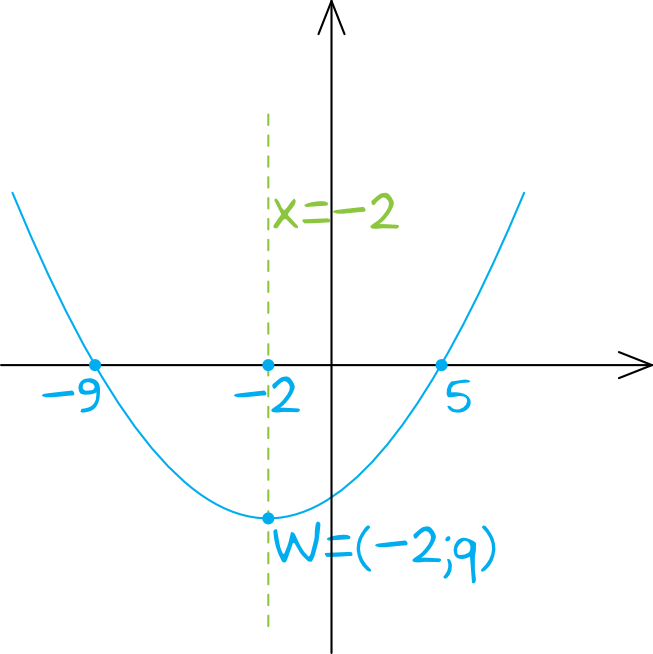
Przykładowo, rozważmy funkcję f(x) = 2x² + 8x - 5. W tym przypadku, a = 2, b = 8, a c = -5. Zatem, oś symetrii to prosta o równaniu x = -8 / (2 * 2) = -8 / 4 = -2. Możemy to sprawdzić, przekształcając funkcję do postaci kanonicznej. Uzupełniając do pełnego kwadratu, otrzymujemy f(x) = 2(x + 2)² - 13. Widzimy, że wierzchołek paraboli znajduje się w punkcie (-2, -13), co potwierdza, że oś symetrii to prosta x = -2.

Funkcje kwadratowe to tylko jeden przykład. Czy istnieją inne typy funkcji, które posiadają oś symetrii? Tak, oczywiście! Funkcje parzyste, jak już wspomnieliśmy, zawsze mają oś symetrii w postaci osi Y. Innym przykładem są funkcje trygonometryczne, takie jak cosinus. Funkcja cos(x) jest funkcją parzystą, więc jej wykresem jest symetryczny względem osi Y. Istnieją również inne funkcje, które mogą posiadać osie symetrii, choć nie zawsze łatwo je zidentyfikować.

Wykorzystanie Osi Symetrii w Analizie Funkcji

Znajomość osi symetrii funkcji może być bardzo pomocna w jej analizie. Po pierwsze, pozwala nam na szybsze szkicowanie wykresu funkcji. Jeśli znamy oś symetrii i kilka punktów na wykresie po jednej stronie osi, możemy łatwo narysować symetryczne punkty po drugiej stronie i uzyskać pełny obraz funkcji. Po drugie, oś symetrii może pomóc w znajdowaniu ekstremów funkcji. W przypadku funkcji kwadratowej, wierzchołek paraboli (który leży na osi symetrii) jest punktem ekstremalnym - minimum, jeśli parabola jest skierowana w górę, lub maksimum, jeśli parabola jest skierowana w dół. Po trzecie, oś symetrii może ułatwić rozwiązywanie równań i nierówności związanych z funkcją. Na przykład, jeśli szukamy rozwiązań równania f(x) = k, gdzie k jest stałą, a funkcja f(x) posiada oś symetrii, możemy wykorzystać tę symetrię do znalezienia drugiego rozwiązania, jeśli znamy jedno. Jeśli x₁ jest rozwiązaniem równania f(x) = k, a oś symetrii to prosta x = a, to drugie rozwiązanie to x₂ = 2a - x₁. Wynika to z faktu, że odległość punktu x₁ od osi symetrii jest taka sama, jak odległość punktu x₂ od tej osi.

Podsumowując, pojęcie osi symetrii wykresu funkcji jest bardzo ważne w matematyce. Pozwala nam lepiej zrozumieć własności funkcji, ułatwia szkicowanie wykresów, znajdowanie ekstremów i rozwiązywanie równań. Warto zapamiętać, że funkcja parzysta ma oś symetrii w osi Y (x=0), a dla funkcji kwadratowej w postaci ogólnej f(x)=ax²+bx+c osią symetrii jest prosta x=-b/2a. Zrozumienie i wykorzystywanie pojęcia osi symetrii znacznie ułatwia analizę funkcji i rozwiązywanie problemów matematycznych.