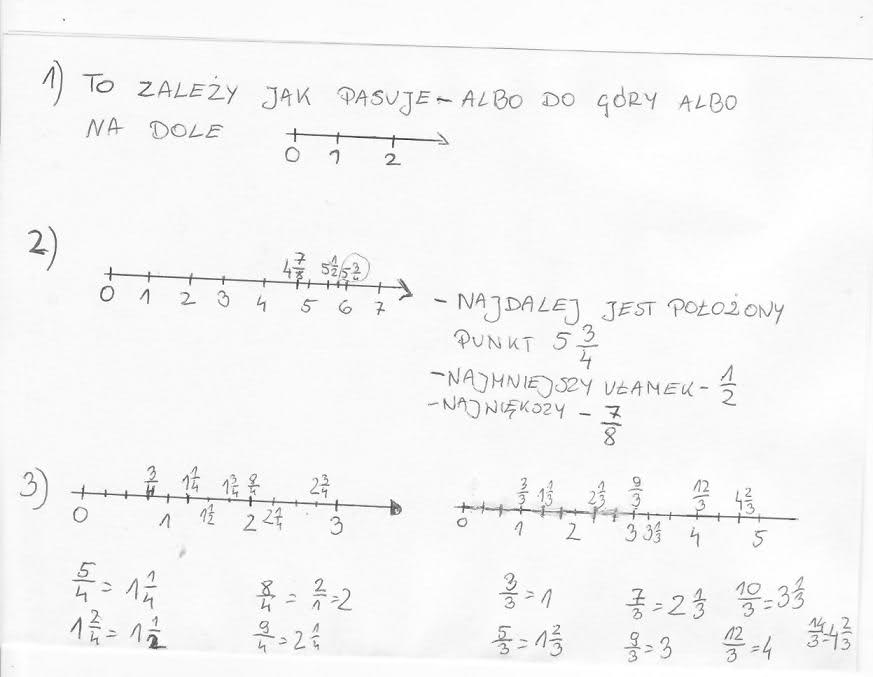
Oś Liczbowa Zadania Klasa 8

Cześć! Rozumiem, że zmagasz się z osią liczbową w klasie 8. To normalne! Wielu uczniów ma z tym trudności. Chcę Ci pokazać, że to wcale nie musi być takie straszne, a wręcz przeciwnie – może stać się całkiem zrozumiałe i nawet… ciekawe! Spróbujemy podejść do tego tematu praktycznie, krok po kroku, żebyś czuł się pewniej na sprawdzianach i w życiu codziennym.

Dlaczego Oś Liczbowa Jest Ważna?

Może się wydawać, że oś liczbowa to tylko linia z liczbami, ale to o wiele więcej! To podstawa do zrozumienia wielu zagadnień matematycznych, a także umiejętność przydatna w życiu codziennym.

Real-world impact: Wyobraź sobie, że planujesz budżet. Musisz uwzględnić zarówno dochody (liczby dodatnie), jak i wydatki (liczby ujemne). Oś liczbowa pomaga wizualizować, gdzie jesteś "na plusie" czy "na minusie". Podobnie, gdy śledzisz zmiany temperatury, wysokość nad poziomem morza, czy analizujesz wyniki sportowe – oś liczbowa ułatwia porównywanie i interpretację danych.

Podstawy algebry: Rozwiązywanie równań i nierówności staje się prostsze, gdy wiesz, jak zaznaczać rozwiązania na osi liczbowej.
Geometria analityczna: Określanie współrzędnych punktów, długości odcinków, czy położenia figur geometrycznych opiera się na osi liczbowej.
Życie codzienne: Planowanie finansów, analiza danych statystycznych, odczytywanie temperatury – to tylko niektóre sytuacje, w których oś liczbowa okazuje się przydatna.

Zasady Działania Osi Liczbowej

Zanim przejdziemy do zadań, przypomnijmy sobie podstawowe zasady:

Punkt zero (0): To punkt odniesienia, od którego zaczynamy liczyć.
Liczby dodatnie: Znajdują się na prawo od zera. Im dalej od zera, tym większa liczba.
Liczby ujemne: Znajdują się na lewo od zera. Im dalej od zera, tym mniejsza liczba (np. -5 jest mniejsze niż -2).
Skala: Odległość między kolejnymi liczbami na osi musi być taka sama (np. 1 cm = 1 jednostka).

Zaznaczanie Liczb na Osi

To proste! Znajdź odpowiednie miejsce na osi i zaznacz kropką. Pamiętaj o zachowaniu odpowiedniej skali.

Przykład: Zaznacz liczby 3, -2, 0, 5 na osi liczbowej.

Zacznij od zera. 3 znajduje się 3 jednostki na prawo od zera. -2 znajduje się 2 jednostki na lewo od zera. 5 znajduje się 5 jednostek na prawo od zera.

Zadania z Osią Liczbową – Krok po Kroku

Teraz przejdźmy do konkretnych zadań. Postaram się wyjaśnić je jak najprościej.

Zadanie 1: Porównywanie Liczb

Zadanie: Która liczba jest większa: -4 czy -1?

Rozwiązanie: Zaznacz te liczby na osi. -1 znajduje się bliżej zera niż -4. Im bliżej zera, tym większa liczba ujemna. Zatem -1 jest większe od -4.

Zadanie 2: Działania na Osi Liczbowej

Zadanie: Oblicz 2 + (-5) na osi liczbowej.

Rozwiązanie:

Zacznij od liczby 2 (zaznacz ją na osi).
Dodawanie liczby ujemnej to to samo, co odejmowanie liczby dodatniej. Zatem musisz przesunąć się o 5 jednostek w lewo.
Kończysz na liczbie -3. Zatem 2 + (-5) = -3.

Zadanie 3: Rozwiązywanie Nierówności

Zadanie: Zaznacz na osi liczbowej zbiór rozwiązań nierówności x > -2.

Rozwiązanie:

Znajdź liczbę -2 na osi.
Ponieważ nierówność jest ostra (x większe od -2, a nie większe lub równe), narysuj otwarte kółko nad -2 (to oznacza, że -2 nie należy do zbioru rozwiązań).
Zaznacz strzałką wszystkie liczby na prawo od -2 (to oznacza, że wszystkie liczby większe od -2 należą do zbioru rozwiązań).

Zadanie 4: Rozwiązywanie Nierówności z Wartością Bezwzględną

Zadanie: Zaznacz na osi liczbowej zbiór rozwiązań nierówności |x| ≤ 3.

Rozwiązanie:

Wartość bezwzględna liczby to jej odległość od zera. Zatem szukamy wszystkich liczb, których odległość od zera jest mniejsza lub równa 3.
Znajdź liczby 3 i -3 na osi.
Ponieważ nierówność jest nieostra (mniejsze lub równe), narysuj zamknięte kółka nad 3 i -3 (to oznacza, że 3 i -3 należą do zbioru rozwiązań).
Zaznacz odcinek między -3 a 3 (to oznacza, że wszystkie liczby między -3 a 3, włącznie z -3 i 3, należą do zbioru rozwiązań).

Typowe Błędy i Jak Ich Unikać

Wiem, że czasami popełnia się błędy. Oto kilka typowych i sposoby, jak ich unikać:

Pomylenie liczb ujemnych i dodatnich: Zawsze pamiętaj, że liczby ujemne są mniejsze od zera, a im dalej od zera w lewo, tym liczba jest mniejsza.
Niewłaściwa skala: Upewnij się, że odległość między kolejnymi liczbami na osi jest taka sama.
Zapominanie o otwartych/zamkniętych kółkach w nierównościach: Otwarte kółko oznacza, że liczba nie należy do zbioru rozwiązań, a zamknięte kółko oznacza, że należy.
Błędne wykonywanie działań: Uważaj na znaki! Dodawanie liczby ujemnej to odejmowanie, a odejmowanie liczby ujemnej to dodawanie.

Counterpoints: A Co, Jeśli Wolę Inne Metody?

Niektórzy uważają, że oś liczbowa jest przestarzała i istnieją lepsze sposoby na zrozumienie liczb. To prawda, istnieją inne metody, ale oś liczbowa jest wizualnym narzędziem, które pomaga w zrozumieniu podstawowych koncepcji. Daje solidny fundament, na którym można budować bardziej zaawansowane umiejętności.

Pamiętaj o Ćwiczeniu!

Matematyka to umiejętność, którą trzeba ćwiczyć. Im więcej zadań zrobisz, tym lepiej zrozumiesz oś liczbową. Nie bój się pytać nauczyciela lub kolegów, jeśli czegoś nie rozumiesz. Korzystaj z podręczników, internetowych zasobów edukacyjnych, i rozwiązuj zadania krok po kroku.

Podsumowanie: Oś liczbowa to ważne narzędzie, które pomaga zrozumieć relacje między liczbami. Ćwicz regularnie, a zobaczysz, że zadania staną się coraz łatwiejsze.

Co Dalej?

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć oś liczbową. Teraz spróbuj rozwiązać kilka zadań samodzielnie. Jeśli nadal masz pytania, poszukaj dodatkowych materiałów w Internecie lub zapytaj nauczyciela. Pamiętaj, że kluczem do sukcesu jest praktyka!

Jakie zagadnienie związane z osią liczbową sprawia Ci największe trudności? Może poświęcimy mu więcej uwagi?