Oś Liczbowa Odległość Liczb Na Osi Liczbowej Klasa 7

Oś liczbowa to fundamentalne narzędzie w matematyce, które pozwala nam wizualizować i porządkować liczby. W klasie 7 zgłębianie jej tajników otwiera drzwi do bardziej zaawansowanych koncepcji. Przyjrzyjmy się zatem, jak efektywnie wykorzystywać oś liczbową, szczególnie skupiając się na pojęciu odległości między liczbami.

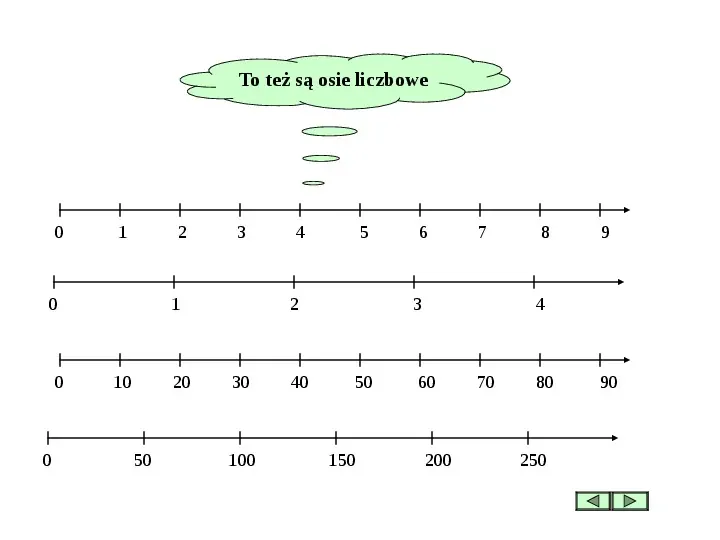
Oś liczbowa, w najprostszej postaci, to prosta, na której zaznaczone są liczby w równych odstępach. Centralnym punktem jest zero (0), od którego w prawo znajdują się liczby dodatnie, a w lewo – liczby ujemne. Ważne jest, aby pamiętać o kilku podstawowych zasadach. Po pierwsze, odstępy między kolejnymi liczbami muszą być równe. Po drugie, strzałka na końcu osi wskazuje kierunek, w którym liczby rosną. Po trzecie, każda liczba ma swoje jednoznaczne położenie na osi.

Zaznaczanie liczb na osi liczbowej jest proste. Wybieramy odpowiednią jednostkę miary (np. jeden centymetr odpowiada jednemu) i odmierzamy od zera odległość proporcjonalną do wartości liczby. Liczby dodatnie zaznaczamy po prawej stronie zera, a liczby ujemne po lewej. Przykładowo, aby zaznaczyć liczbę 3, odmierzamy trzy jednostki w prawo od zera. Aby zaznaczyć liczbę -2, odmierzamy dwie jednostki w lewo od zera.

Oś liczbowa pozwala nam wizualizować kolejność liczb. Liczba znajdująca się bardziej na prawo jest większa od liczby znajdującej się bardziej na lewo. Na przykład, 5 jest większe od 2, a -1 jest większe od -4. Pozwala to na łatwe porównywanie liczb i rozstrzyganie, która z nich jest większa lub mniejsza.

Odległość między liczbami na osi liczbowej

Odległość między dwiema liczbami na osi liczbowej to wartość bezwzględna różnicy tych liczb. Oznacza to, że niezależnie od tego, która liczba jest większa, a która mniejsza, wynik zawsze będzie dodatni. Formalnie, jeśli mamy dwie liczby a i b, to odległość między nimi wynosi |a - b|.

Aby obliczyć odległość między dwiema liczbami, odejmujemy od siebie te liczby, a następnie obliczamy wartość bezwzględną wyniku. Wartość bezwzględna liczby to jej odległość od zera, zawsze wyrażona liczbą nieujemną. Zatem, |5| = 5, a |-5| = 5.

Przykład 1: Oblicz odległość między liczbami 7 i 2.

|7 - 2| = |5| = 5

Odległość między liczbami 7 i 2 wynosi 5.

Przykład 2: Oblicz odległość między liczbami -3 i 4.

|-3 - 4| = |-7| = 7

Odległość między liczbami -3 i 4 wynosi 7.

Przykład 3: Oblicz odległość między liczbami -5 i -1.

|-5 - (-1)| = |-5 + 1| = |-4| = 4

Odległość między liczbami -5 i -1 wynosi 4.

Zauważmy, że kolejność odejmowania nie ma znaczenia, ponieważ wartość bezwzględna "eliminuje" znak ujemny. Możemy więc obliczyć |2 - 7| = |-5| = 5 i otrzymamy ten sam wynik.

Wartość bezwzględna ma wiele zastosowań w matematyce. Używamy jej do definiowania odległości, modułów liczb zespolonych, a także w wielu algorytmach.

Praktyczne zastosowania osi liczbowej i odległości

Oś liczbowa i pojęcie odległości między liczbami mają wiele praktycznych zastosowań. Możemy je wykorzystać do rozwiązywania różnych problemów, zarówno matematycznych, jak i związanych z życiem codziennym.

Przykładowo, wyobraźmy sobie, że mamy na osi liczbowej zaznaczone temperatury w różnych miastach. Możemy łatwo odczytać temperaturę w każdym mieście i obliczyć różnicę temperatur między nimi, korzystając z pojęcia odległości.

Innym przykładem może być problem związany z czasem. Załóżmy, że Janek zaczął czytać książkę o godzinie 10:00, a skończył o godzinie 13:00. Możemy przedstawić to na osi liczbowej, gdzie każda godzina to kolejna liczba. Odległość między liczbami 10 i 13 to 3, co oznacza, że Janek czytał książkę przez 3 godziny.

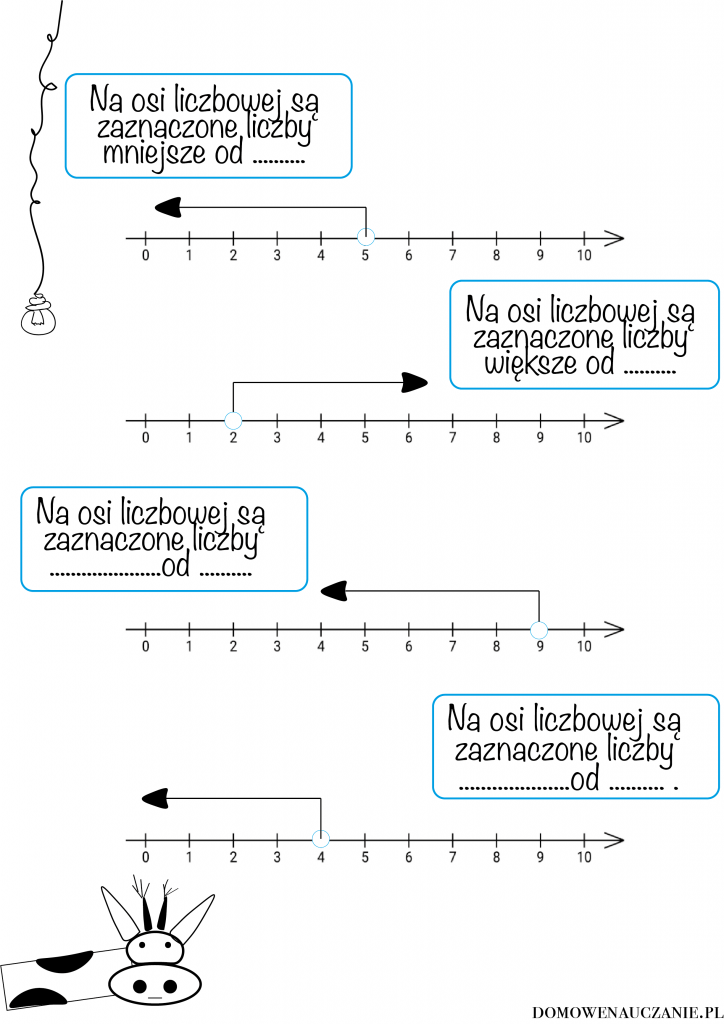
Oś liczbowa przydaje się również w rozwiązywaniu nierówności. Możemy zaznaczyć na osi zbiór liczb spełniających daną nierówność, co ułatwia jej wizualizację i zrozumienie. Na przykład, nierówność x > 2 oznacza, że rozwiązaniem są wszystkie liczby większe od 2. Zaznaczamy to na osi liczbowej, rysując otwarte kółko nad liczbą 2 (ponieważ 2 nie należy do zbioru rozwiązań) i strzałkę w prawo, wskazującą na wszystkie liczby większe od 2.

Podobnie, nierówność x ≤ -1 oznacza, że rozwiązaniem są wszystkie liczby mniejsze lub równe -1. Zaznaczamy to na osi liczbowej, rysując zamknięte kółko nad liczbą -1 (ponieważ -1 należy do zbioru rozwiązań) i strzałkę w lewo, wskazującą na wszystkie liczby mniejsze od -1.

Rozwiązywanie zadań z osią liczbową często wymaga logicznego myślenia i umiejętności interpretacji danych. Ważne jest, aby dokładnie przeczytać treść zadania i zrozumieć, co jest wymagane. Następnie należy odpowiednio zaznaczyć liczby i przedziały na osi liczbowej i wykorzystać pojęcie odległości do rozwiązania problemu.

Umiejętność korzystania z osi liczbowej to cenna umiejętność, która przydaje się nie tylko w matematyce, ale również w życiu codziennym. Pozwala na lepsze zrozumienie liczb, ich kolejności i wzajemnych relacji. Ćwiczenie i rozwiązywanie różnych zadań z wykorzystaniem osi liczbowej pozwala na utrwalenie wiedzy i rozwinięcie umiejętności logicznego myślenia.

Pamiętaj, oś liczbowa to Twoje narzędzie. Im lepiej się z nim zapoznasz, tym łatwiej będzie Ci rozwiązywać problemy matematyczne. Zatem, weź ołówek, linijkę i kartkę papieru i zacznij ćwiczyć! Im więcej ćwiczysz, tym pewniej będziesz się czuł z osią liczbową i jej zastosowaniami. Powodzenia!