Odległość Punktu Od Prostej Wzor

Czy kiedykolwiek stanąłeś przed problemem obliczenia najkrótszej odległości między jakimś punktem a linią prostą? Może podczas planowania układu mebli w pokoju, projektowania ogrodu, a nawet programowania gier komputerowych? To zaskakująco powszechny problem, a na szczęście istnieje na niego prosty i elegancki wzór. Zrozumienie go otwiera drzwi do wielu zastosowań w życiu codziennym i różnych dziedzinach nauki.

W tym artykule rozłożymy ten wzór na czynniki pierwsze, wyjaśniając krok po kroku, jak go używać i co ważniejsze, dlaczego on działa. Nie martw się, jeśli matematyka nie jest Twoją najmocniejszą stroną. Postaramy się unikać zbędnego żargonu i skupić się na praktycznym zastosowaniu. Chcesz wiedzieć, jak szybko i dokładnie obliczyć odległość punktu od prostej? Zaczynamy!

Zrozumienie Problemu

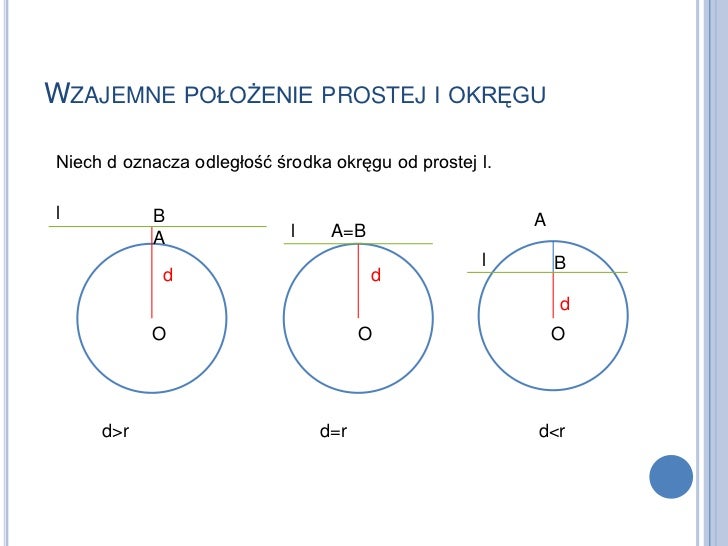
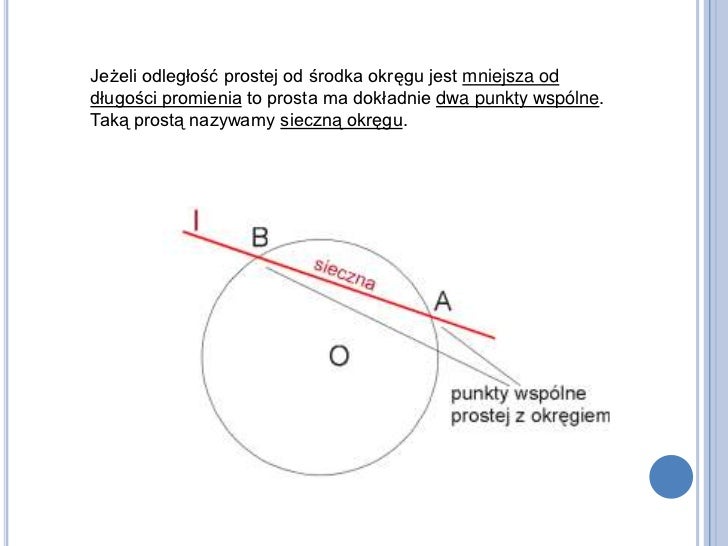
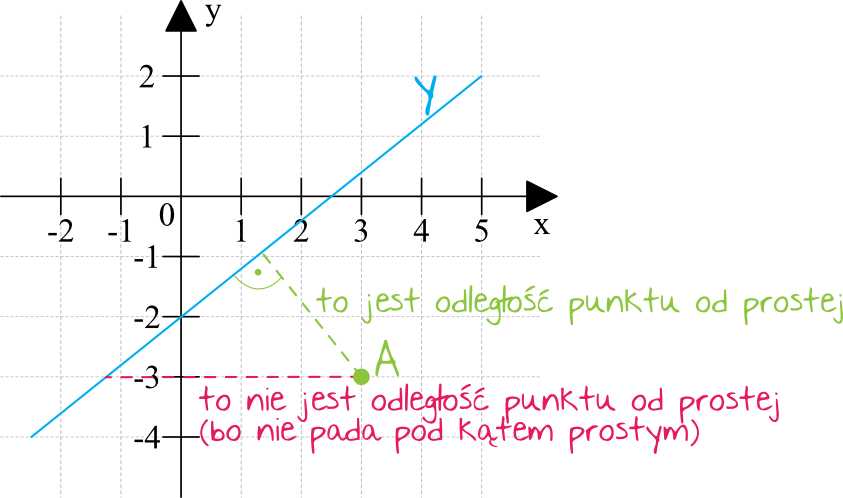
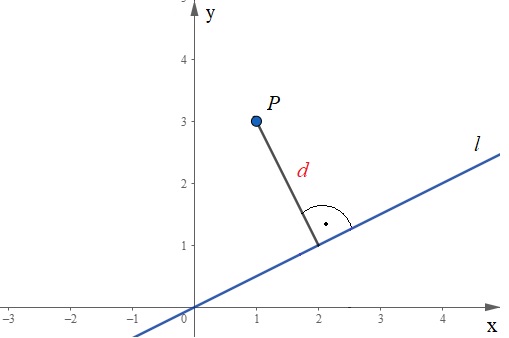
Wyobraź sobie, że masz punkt na kartce papieru i narysowaną linię prostą. Chcesz zmierzyć odległość między nimi. Mogłeśbyś po prostu wziąć linijkę i spróbować zmierzyć odległość "na oko", ale to byłoby niedokładne. Co więcej, pytanie brzmi, który odcinek zmierzyć? Od punktu do prostej można narysować nieskończenie wiele odcinków. Który z nich jest najkrótszy?

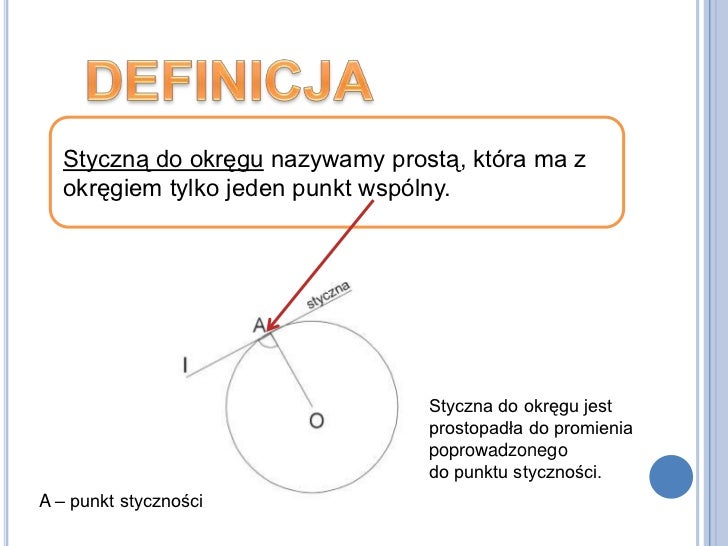
Kluczem jest zrozumienie, że najkrótsza odległość to zawsze odcinek prostopadły do prostej, wychodzący z naszego punktu. To on tworzy kąt prosty (90 stopni) z daną prostą. Teraz musimy znaleźć sposób, aby obliczyć długość tego odcinka bez konieczności rysowania go i mierzenia.

Wzór na Odległość Punktu od Prostej

Wzór, o którym mówimy, wygląda następująco:

d = |Ax₀ + By₀ + C| / √(A² + B²)

Gdzie:

d - to szukana odległość.
(x₀, y₀) - to współrzędne punktu, od którego mierzymy odległość.
Ax + By + C = 0 - to równanie prostej w postaci ogólnej.
|...| - oznacza wartość bezwzględną (czyli wynik zawsze będzie dodatni).

Brzmi skomplikowanie? Spokojnie, rozłóżmy to na mniejsze kawałki.

Równanie Ogólne Prostej

Zanim zaczniemy obliczenia, musimy się upewnić, że nasze równanie prostej jest w formie ogólnej: Ax + By + C = 0. To ważne, ponieważ wartości A, B i C, które wstawimy do wzoru, pochodzą właśnie z tej formy równania.

Jeśli masz równanie prostej w innej formie, np. w postaci kierunkowej (y = mx + b), musisz je przekształcić do formy ogólnej. To zwykle polega na przeniesieniu wszystkich składników na jedną stronę równania, tak aby po drugiej stronie zostało zero.

Przykład:

Jeśli mamy równanie y = 2x + 3, przekształcamy je następująco:

-2x + y - 3 = 0

Teraz możemy odczytać: A = -2, B = 1, C = -3.

Krok po Kroku: Obliczanie Odległości

Teraz gdy rozumiemy już wzór i równanie prostej, możemy przejść do obliczeń.

Określ współrzędne punktu (x₀, y₀). To punkt, od którego chcesz zmierzyć odległość.
Znajdź równanie prostej w postaci ogólnej (Ax + By + C = 0). Jeśli masz je w innej formie, przekształć je.
Podstaw wartości A, B, C, x₀ i y₀ do wzoru. Pamiętaj o kolejności działań.
Oblicz wartość wyrażenia w liczniku (Ax₀ + By₀ + C).
Weź wartość bezwzględną wyniku z kroku 4 (|Ax₀ + By₀ + C|). To zapewnia, że odległość będzie zawsze dodatnia.
Oblicz wartość wyrażenia w mianowniku (√(A² + B²)). Najpierw oblicz kwadraty A i B, potem dodaj je, a na końcu wyciągnij pierwiastek kwadratowy.
Podziel wartość bezwzględną z licznika przez wartość z mianownika. Wynik to szukana odległość.

Przykład Praktyczny

Powiedzmy, że chcemy obliczyć odległość punktu P(2, 3) od prostej o równaniu 3x + 4y - 5 = 0.

Punkt: (x₀, y₀) = (2, 3)
Równanie prostej: 3x + 4y - 5 = 0 (A = 3, B = 4, C = -5)
Podstawiamy do wzoru: d = |(3 * 2) + (4 * 3) - 5| / √(3² + 4²)
Obliczamy licznik: |6 + 12 - 5| = |13| = 13
Obliczamy mianownik: √(9 + 16) = √25 = 5
Dzielimy: d = 13 / 5 = 2.6

Czyli odległość punktu P(2, 3) od prostej 3x + 4y - 5 = 0 wynosi 2.6 jednostek.

Dlaczego Ten Wzór Działa? (Trochę Teorii)

Wzór na odległość punktu od prostej nie bierze się znikąd. Jego wyprowadzenie opiera się na kilku kluczowych konceptach z geometrii analitycznej i algebry liniowej.

Choć pełne wyprowadzenie może być dość skomplikowane, możemy zrozumieć jego intuicję. Wyobraźmy sobie, że chcemy znaleźć punkt na prostej, który jest najbliżej naszego punktu P(x₀, y₀). Możemy to zrobić, znajdując rzut prostokątny punktu P na daną prostą. Wzór, który używamy, w gruncie rzeczy wykorzystuje wektory i ich własności, aby obliczyć długość tego rzutu - czyli najkrótszą odległość.

Mianownik wzoru (√(A² + B²)) jest związany z długością wektora normalnego do prostej (wektor normalny jest prostopadły do prostej). Licznik, po wzięciu wartości bezwzględnej, daje nam miarę odległości od punktu do prostej w kierunku tego wektora normalnego.

Zrozumienie teorii nie jest niezbędne do używania wzoru, ale może pomóc w zapamiętaniu go i zrozumieniu, dlaczego on działa w określony sposób.

Praktyczne Zastosowania

Wzór na odległość punktu od prostej ma wiele praktycznych zastosowań, zarówno w życiu codziennym, jak i w różnych dziedzinach nauki i technologii.

Geometria obliczeniowa: W grafice komputerowej i robotyce, wzór ten jest używany do wykrywania kolizji, planowania ścieżek i obliczania odległości między obiektami.
Fizyka: W fizyce, wzór ten może być używany do obliczania odległości między cząstką a polem sił, lub do analizy ruchu w przestrzeni.
Inżynieria: W inżynierii budowlanej, wzór ten może być używany do obliczania odległości między punktem a powierzchnią (która może być aproksymowana przez płaszczyznę), co jest przydatne przy projektowaniu i budowie konstrukcji.
Nawigacja: W systemach nawigacyjnych, wzór ten może być używany do obliczania odległości od punktu (np. samochodu) do drogi (która może być aproksymowana przez linię prostą).
Statystyka: W analizie danych, wzór ten może być używany do obliczania odległości między punktem danych a linią trendu, co jest przydatne przy ocenie dopasowania modelu do danych.

To tylko kilka przykładów. Im głębiej wejdziesz w różne dziedziny, tym więcej zastosowań tego wzoru odkryjesz.

Podsumowanie i Wskazówki

Obliczanie odległości punktu od prostej za pomocą wzoru d = |Ax₀ + By₀ + C| / √(A² + B²) to potężne narzędzie, które ma zastosowanie w wielu dziedzinach. Pamiętaj o kilku kluczowych kwestiach:

Upewnij się, że równanie prostej jest w postaci ogólnej (Ax + By + C = 0).
Pamiętaj o wartości bezwzględnej w liczniku.
Zrozumienie, *dlaczego* wzór działa, może pomóc w jego zapamiętaniu i stosowaniu.
Ćwicz! Im więcej przykładów rozwiążesz, tym pewniej będziesz się czuł.

Mamy nadzieję, że ten artykuł pomógł Ci zrozumieć wzór na odległość punktu od prostej i jego zastosowania. Nie bój się eksperymentować i szukać własnych przykładów, gdzie możesz go wykorzystać. Powodzenia!