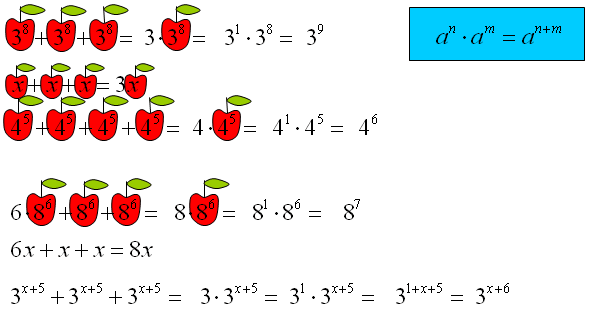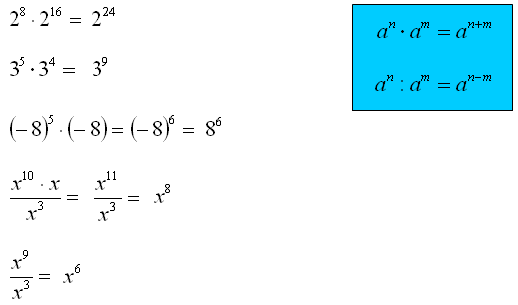Odejmowanie Potęg O Tych Samych Podstawach

Witajcie! Dziś zajmiemy się odejmowaniem potęg o tych samych podstawach. Choć brzmi to skomplikowanie, w rzeczywistości jest to prosty i bardzo użyteczny element algebry, który znajdzie zastosowanie w wielu dziedzinach.

Co to są potęgi?

Zanim przejdziemy do odejmowania, przypomnijmy sobie, czym w ogóle jest potęga. Potęga to sposób zapisu wielokrotnego mnożenia tej samej liczby przez samą siebie. Zapisujemy ją jako aⁿ, gdzie:

a to podstawa potęgi – liczba, którą mnożymy.
n to wykładnik potęgi – liczba, która mówi nam, ile razy mamy pomnożyć podstawę przez samą siebie.

Na przykład, 2³ oznacza 2 * 2 * 2 = 8. W tym przypadku 2 jest podstawą, a 3 jest wykładnikiem.

Odejmowanie potęg – pułapka!

Ważne jest, żeby od razu zaznaczyć – nie odejmujemy potęg! Nie istnieje prosta reguła na obliczenie aⁿ - a^m. To, o czym będziemy mówić, to dzielenie potęg o tych samych podstawach, a wynik tego dzielenia często przedstawiamy w formie różnicy wykładników.

Dzielenie potęg o tych samych podstawach

Kluczową zasadą, którą musimy zapamiętać, jest: kiedy dzielimy potęgi o tych samych podstawach, odejmujemy ich wykładniki. Formalnie zapisujemy to tak:

aⁿ / a^m = a^n-m

Gdzie a jest dowolną liczbą różną od zera (ponieważ nie możemy dzielić przez zero), a n i m są dowolnymi liczbami całkowitymi.

Przykłady

Spójrzmy na kilka przykładów, aby lepiej zrozumieć tę zasadę:

Przykład 1: 5⁷ / 5³ = 5^7-3 = 5⁴ = 625
Przykład 2: 2¹⁰ / 2⁶ = 2^10-6 = 2⁴ = 16
Przykład 3: 3⁵ / 3⁵ = 3^5-5 = 3⁰ = 1 (Pamiętajmy, że dowolna liczba (poza zerem) podniesiona do potęgi 0 daje 1)
Przykład 4: 4² / 4⁵ = 4^2-5 = 4^-3 = 1/4³ = 1/64 (Ujemny wykładnik oznacza odwrotność potęgi)

Jak widzimy, zasada jest prosta: dzielimy potęgi o tej samej podstawie, odejmujemy wykładniki. Należy jednak pamiętać o kilku ważnych kwestiach:

Podstawa musi być taka sama: Ta zasada działa tylko, gdy podstawy potęg są identyczne. Nie możemy jej zastosować do wyrażenia typu 2⁵ / 3².
Dzielenie przez zero: Podstawa potęgi (a) nie może być równa zero, ponieważ nie możemy dzielić przez zero.
Ujemne wykładniki: Wynik odejmowania wykładników może być liczbą ujemną. Pamiętajmy, że a^-n = 1/aⁿ.

Wyjaśnienie, dlaczego to działa

Zastanówmy się, dlaczego ta zasada w ogóle działa. Spójrzmy na przykład:

5⁴ / 5² = (5 * 5 * 5 * 5) / (5 * 5)

Możemy uprościć to wyrażenie, skracając te same czynniki w liczniku i mianowniku:

(5 * 5 * 5 * 5) / (5 * 5) = (5 * 5) * (5 * 5) / (5 * 5) = 5 * 5 = 5²

Zauważ, że 5² to to samo, co 5^4-2. Widzimy więc, że odejmowanie wykładników jest skróconym sposobem na uproszczenie wyrażenia, w którym dzielimy potęgi o tych samych podstawach.

Zastosowania praktyczne

Odejmowanie (a właściwie dzielenie) potęg o tych samych podstawach ma wiele zastosowań w różnych dziedzinach, takich jak:

Nauki ścisłe: W fizyce i chemii często spotykamy się z bardzo dużymi lub bardzo małymi liczbami, które wygodnie zapisuje się w notacji naukowej (np. 6.022 x 10²³). Dzielenie liczb zapisanych w notacji naukowej wykorzystuje właśnie zasadę odejmowania wykładników.
Informatyka: W informatyce używamy potęg dwójki do reprezentowania danych. Dzielenie liczb binarnych często sprowadza się do operacji na potęgach dwójki.
Finanse: W obliczeniach związanych z oprocentowaniem składanym lub amortyzacją kredytów, potęgi odgrywają istotną rolę.
Życie codzienne: Nawet bez świadomości, używamy tej zasady w różnych sytuacjach, np. przy skalowaniu przepisów kulinarnych (gdzie składniki są proporcjonalnie zmieniane, co można opisać za pomocą potęg).

Podsumowanie

Podsumowując, choć mówimy o "odejmowaniu potęg", to w rzeczywistości chodzi o dzielenie potęg o tych samych podstawach. Kluczowa zasada to: aⁿ / a^m = a^n-m. Pamiętajmy, że podstawa musi być taka sama i różna od zera, a wykładniki mogą być dowolnymi liczbami całkowitymi (również ujemnymi). Zrozumienie tej zasady jest fundamentem do dalszej nauki algebry i znajdzie zastosowanie w wielu dziedzinach nauki i życia codziennego.