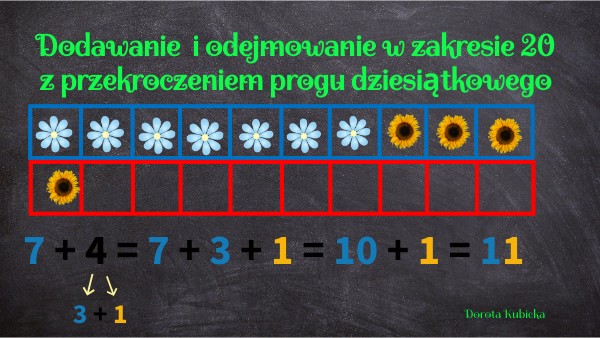
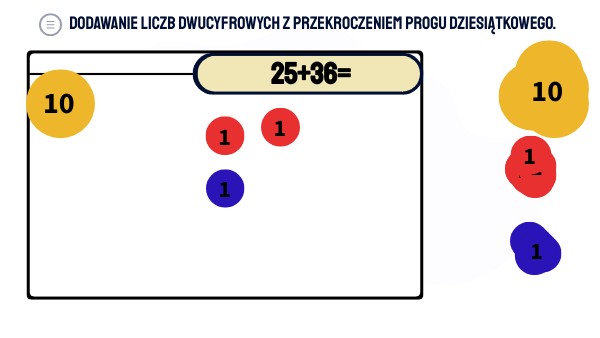
Odejmowanie Liczb W Zakresie 30 Z Przekroczeniem Progu Dziesiątkowego

Witajcie młodzi matematycy! Dzisiaj zajmiemy się bardzo ważnym zagadnieniem: odejmowaniem liczb w zakresie 30 z przekroczeniem progu dziesiątkowego. Brzmi skomplikowanie? Bez obaw, pokażemy krok po kroku, jak to robić w prosty i zrozumiały sposób.

Czym jest odejmowanie z przekroczeniem progu dziesiątkowego?

Zacznijmy od zrozumienia, co to właściwie znaczy "przekroczenie progu dziesiątkowego". Wyobraźcie sobie, że macie liczbę, która jest większa od 10, na przykład 12. Chcecie od niej odjąć pewną liczbę, taką jak 5. Odejmowanie z przekroczeniem progu dziesiątkowego oznacza, że żeby wykonać to odejmowanie, musimy "rozłożyć" liczbę od której odejmujemy na dziesiątkę i resztę, a następnie odjąć od tej dziesiątki. Dajmy na to, jeśli mamy 12 - 5, musimy niejako "pożyczyć" od dziesiątki, bo od 2 nie możemy odjąć 5.

Mówiąc prościej, to sytuacja, w której cyfra jedności w liczbie, od której odejmujemy (odjemna), jest mniejsza niż cyfra jedności liczby, którą odejmujemy (odjemnik). Wtedy, aby wykonać odejmowanie, musimy "pożyczyć" 10 z cyfry dziesiątek.

Definicje:

• Odjemna: Liczba, od której odejmujemy (np. w działaniu 15 - 7, odjemną jest 15).
• Odjemnik: Liczba, którą odejmujemy (np. w działaniu 15 - 7, odjemnikiem jest 7).
• Różnica: Wynik odejmowania (np. w działaniu 15 - 7, różnicą jest 8).
• Próg dziesiątkowy: Granica między kolejnymi dziesiątkami (np. 10, 20, 30). Przekroczenie progu dziesiątkowego następuje, gdy odejmujemy tak, że wynik jest w poprzedniej dziesiątce.

Jak odejmować z przekroczeniem progu dziesiątkowego – krok po kroku:

Przyjrzyjmy się kilku przykładom, żeby lepiej zrozumieć, jak to działa.

Przykład 1: 14 - 6

1. Rozkładamy odjemną: Zastanówmy się, ile dziesiątek i jedności ma liczba 14. Mamy jedną dziesiątkę (10) i cztery jedności (4).
2. Sprawdzamy, czy możemy odjąć jedności: Czy możemy odjąć 6 od 4? Nie, ponieważ 4 jest mniejsze od 6.
3. "Pożyczamy" dziesiątkę: Musimy "pożyczyć" 10 z dziesiątki. Teraz mamy 10 + 4 = 14.
4. Odejmujemy: Odejmujemy 6 od 10: 10 - 6 = 4.
5. Dodajemy resztę jedności: Dodajemy 4 (resztę jedności z początku) do wyniku odejmowania dziesiątki: 4 + 4 = 8.
6. Wynik: 14 - 6 = 8.

Przykład 2: 21 - 5

1. Rozkładamy odjemną: 21 to dwie dziesiątki (20) i jedna jedność (1).
2. Sprawdzamy, czy możemy odjąć jedności: Czy możemy odjąć 5 od 1? Nie, bo 1 jest mniejsze od 5.
3. "Pożyczamy" dziesiątkę: "Pożyczamy" 10 z jednej z dziesiątek. Teraz mamy 10 + 1 = 11.
4. Odejmujemy: Odejmujemy 5 od 10: 10 - 5 = 5. Następnie dodajemy do tego 1 (resztę z jedności) więc 5+1 = 6. A jeśli nie odjęliśmy jeszcze od tej dziesiątki to wtedy 11-5 =6.
5. Uwzględniamy pozostałe dziesiątki: Zostaje nam jeszcze jedna dziesiątka (ponieważ mieliśmy dwie dziesiątki na początku i jedną "pożyczyliśmy").
6. Dodajemy wszystko do siebie: Dziesiątka (10) i reszta z odejmowania (6) czyli 10+6 = 16. Nie, to nie tak! Mieliśmy dwie dziesiątki, jedną "pożyczyliśmy". więc wciąż mamy jedną dziesiątkę z której nic nie odjęliśmy. Powinno być: 11 - 5 = 6 a więc wynik to 16?! Ups! Powinno wyjść 21 - 5 = 16, no tak! Czyli 10 + (11-5) = 10 + 6 = 16.
7. Wynik: 21 - 5 = 16.

Przykład 3: 17 - 9

Spróbujcie sami! Rozłóżcie 17 na dziesiątkę i jedności, sprawdźcie, czy możecie odjąć 9 od 7, "pożyczcie" dziesiątkę i wykonajcie obliczenia. Odpowiedź to 8.

Ćwiczenia praktyczne:

Najlepszym sposobem na opanowanie odejmowania z przekroczeniem progu dziesiątkowego jest ćwiczenie. Oto kilka zadań do samodzielnego rozwiązania:

• 13 - 4 = ?
• 16 - 8 = ?
• 22 - 7 = ?
• 15 - 6 = ?
• 11 - 3 = ?

Sprawdźcie swoje odpowiedzi! (9, 8, 15, 9, 8)

Praktyczne zastosowanie:

Odejmowanie z przekroczeniem progu dziesiątkowego jest bardzo przydatne w życiu codziennym. Wyobraźcie sobie, że macie 15 zł i chcecie kupić zabawkę za 7 zł. Musimy policzyć, ile pieniędzy wam zostanie. To właśnie przykład odejmowania z przekroczeniem progu dziesiątkowego! Albo macie 23 cukierki i dajecie 8 kolegom. Ile wam zostanie? Też odejmowanie z przekroczeniem progu dziesiątkowego.

Odejmowanie z przekroczeniem progu dziesiątkowego to umiejętność, którą warto opanować, bo przydaje się w wielu sytuacjach!

Dodatkowe wskazówki:

Pamiętajcie, że praktyka czyni mistrza! Im więcej będziecie ćwiczyć, tym łatwiej wam pójdzie odejmowanie z przekroczeniem progu dziesiątkowego. Powodzenia!