Odcinki W Graniastosłupach Klasa 8

Witajcie, drodzy uczniowie klasy 8! Zapewne zmagacie się właśnie z geometrią przestrzenna i graniastosłupami. Wiem, że może to być trudne – wyobrażenie sobie brył 3D na płaskim papierze, obliczanie długości odcinków, kątów... Nie martwcie się! Razem postaramy się to zrozumieć. Chciałbym Wam pomóc rozjaśnić kwestię odcinków w graniastosłupach, tak abyście czuli się pewniej na lekcjach i kartkówkach.

Geometria to nie tylko wzory i definicje. Wyobraźcie sobie, że budujecie domek dla ptaków. Graniastosłupy są wszędzie – kształt dachu, ścian, nawet podstawa może mieć formę graniastosłupa. Zrozumienie zasad geometrii pozwoli Wam lepiej planować i budować, a także dostrzegać piękno i porządek w otaczającym świecie. Dzięki zrozumieniu graniastosłupów lepiej poradzicie sobie w życiu codziennym, np. przy obliczaniu objętości pudełek lub szacowaniu ilości materiałów potrzebnych do remontu.

Czym jest graniastosłup?

Zacznijmy od podstaw. Graniastosłup to bryła, która ma dwie identyczne, równoległe podstawy (wielokąty) połączone ścianami bocznymi, które są równoległobokami. Najprościej mówiąc, to taka "wieża" zbudowana na jakimś wielokącie.

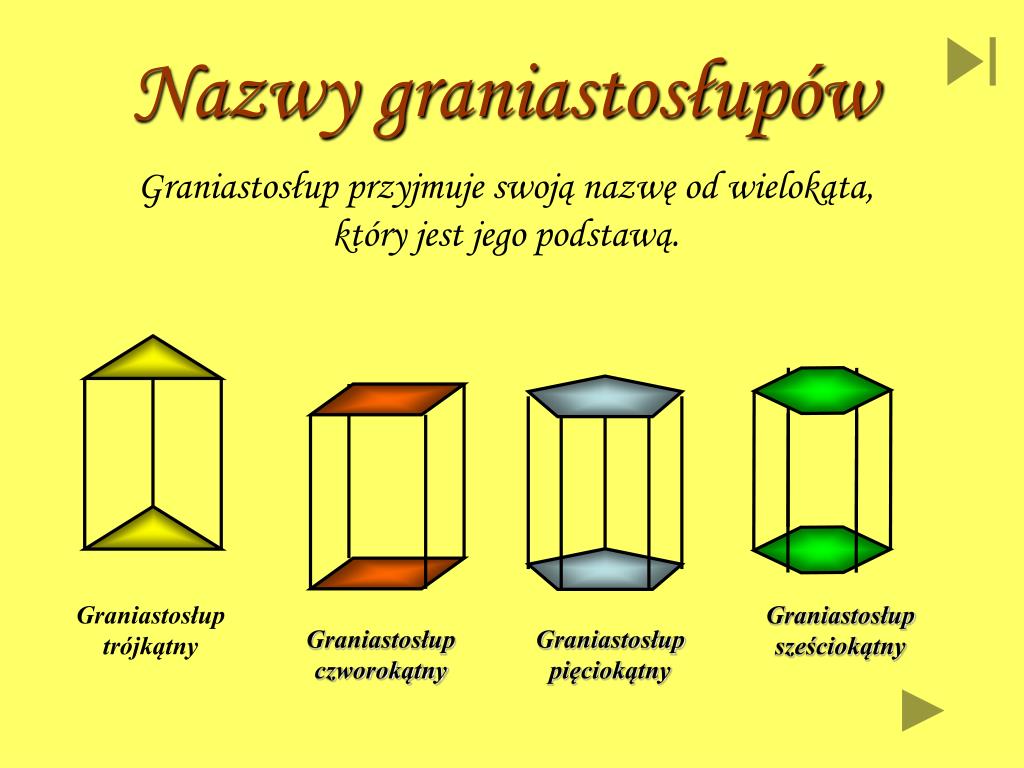
Istnieją różne rodzaje graniastosłupów, zależne od kształtu podstawy:

Graniastosłup trójkątny: Podstawa to trójkąt.
Graniastosłup czworokątny: Podstawa to czworokąt (np. kwadrat, prostokąt, trapez). Szczególnym przypadkiem jest prostopadłościan, który ma wszystkie ściany prostokątne, oraz sześcian, który ma wszystkie ściany kwadratowe.
Graniastosłup pięciokątny: Podstawa to pięciokąt.
I tak dalej...

Ważne jest, aby pamiętać o kilku elementach graniastosłupa:

Podstawy: Dwa identyczne wielokąty, leżące naprzeciwko siebie.
Ściany boczne: Równoległoboki łączące podstawy.
Krawędzie: Linie, w których ściany się spotykają.
Wierzchołki: Punkty, w których zbiegają się krawędzie.
Wysokość: Odległość między podstawami.

Odcinki w graniastosłupach – Kluczowe pojęcia

Teraz przejdźmy do sedna: odcinki w graniastosłupach. Musimy rozróżnić kilka typów odcinków, które często pojawiają się w zadaniach:

Krawędzie podstawy

To odcinki, które tworzą wielokąt będący podstawą graniastosłupa. Ich długości zależą od rodzaju wielokąta w podstawie. Na przykład, w graniastosłupie prawidłowym czworokątnym (prostopadłościanie) o podstawie kwadratu, wszystkie krawędzie podstawy mają taką samą długość.

Przykładowo, jeśli mamy graniastosłup trójkątny, którego podstawa jest trójkątem równobocznym o boku 5 cm, to każda krawędź podstawy ma długość 5 cm.

Krawędzie boczne

To odcinki, które łączą odpowiadające sobie wierzchołki obu podstaw. Są one równoległe i mają taką samą długość, równą wysokości graniastosłupa. W graniastosłupach prostych, krawędzie boczne są prostopadłe do podstaw.

Wyobraźcie sobie, że graniastosłup to budynek. Krawędzie boczne to filary, które podtrzymują dach (górną podstawę).

Przekątne podstawy

To odcinki łączące nie sąsiednie wierzchołki podstawy. Przekątne istnieją tylko wtedy, gdy podstawa jest wielokątem o co najmniej czterech bokach (czyli czworokątem, pięciokątem, itd.).

Na przykład, w graniastosłupie, którego podstawą jest prostokąt o bokach 3 cm i 4 cm, długość przekątnej podstawy możemy obliczyć z twierdzenia Pitagorasa: √(3² + 4²) = √(9 + 16) = √25 = 5 cm.

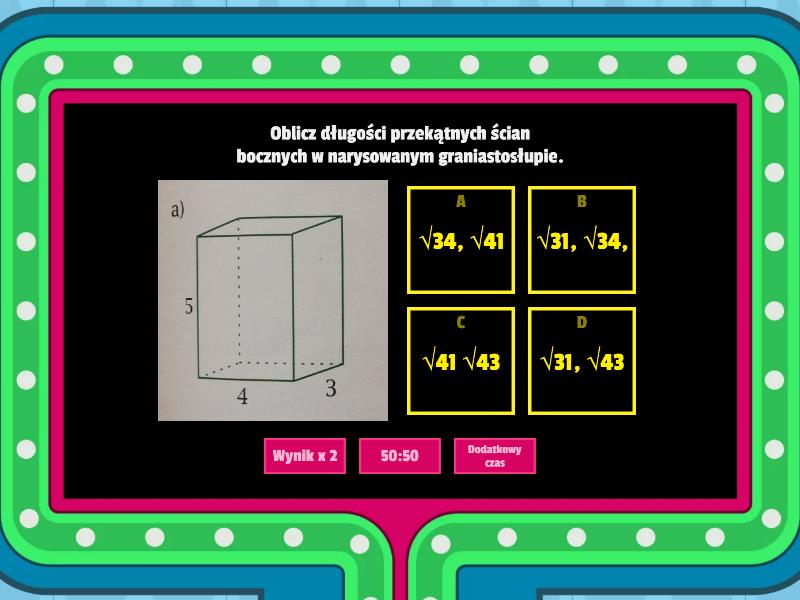
Przekątne ścian bocznych

To odcinki łączące nie sąsiednie wierzchołki na ścianie bocznej. Każda ściana boczna jest równoległobokiem, więc ma dwie przekątne. Ich długość zależy od długości krawędzi podstawy i wysokości graniastosłupa oraz kąta nachylenia ściany bocznej (jeśli graniastosłup nie jest prosty).

Jeśli mamy prostopadłościan o wymiarach 3 cm x 4 cm x 5 cm (długość, szerokość, wysokość), to przekątna ściany o wymiarach 4 cm x 5 cm ma długość √(4² + 5²) = √41 cm.

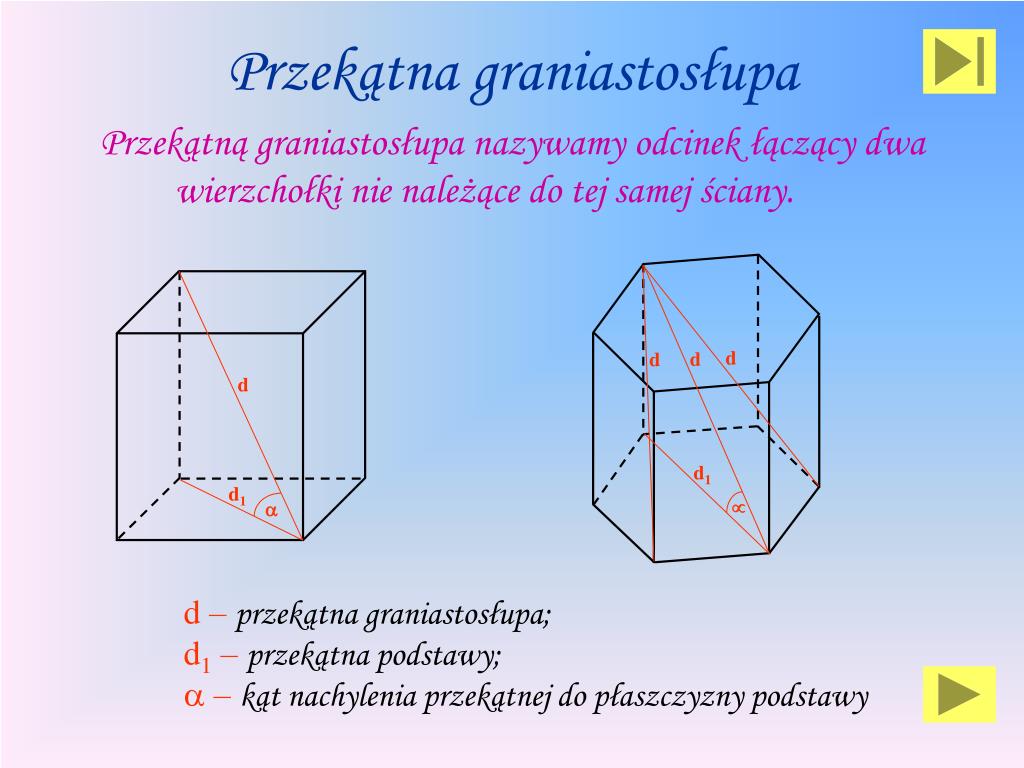
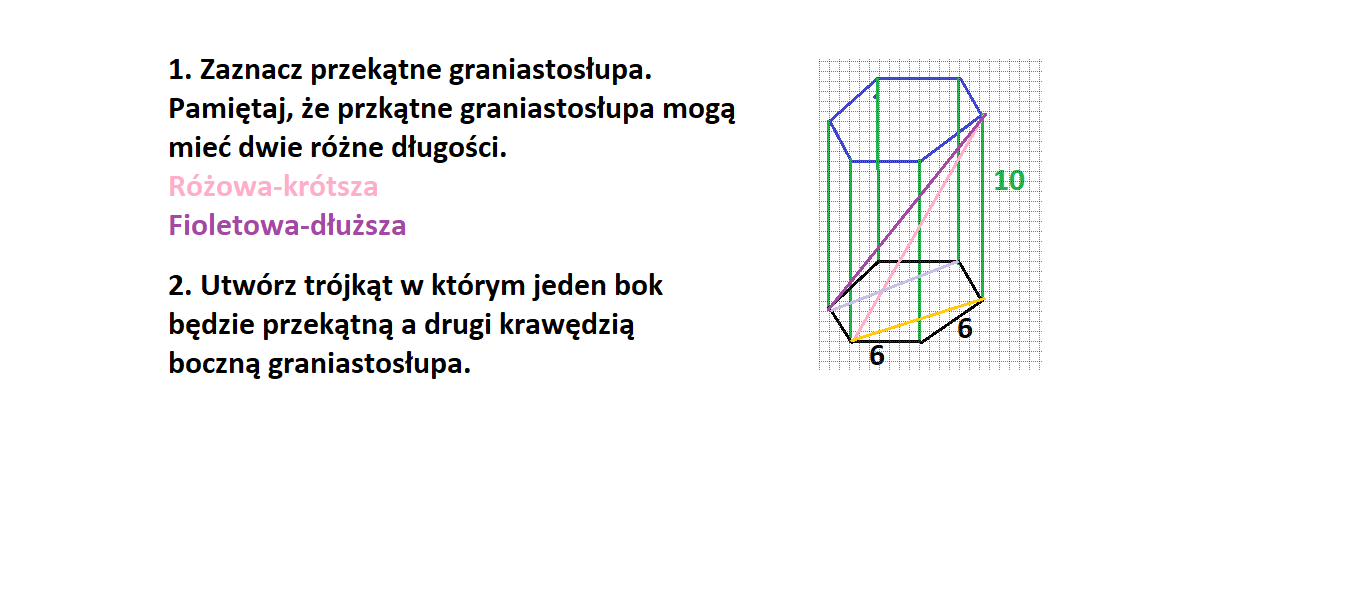
Przekątna graniastosłupa

To odcinek łączący dwa wierzchołki graniastosłupa, które nie leżą na tej samej ścianie (ani w tej samej podstawie). Obliczenie długości przekątnej graniastosłupa może być bardziej skomplikowane i często wymaga użycia twierdzenia Pitagorasa dwukrotnie.

Wyobraźcie sobie, że przekątna graniastosłupa przecina wnętrze bryły, łącząc najdalsze punkty.

Jak obliczać długości odcinków?

Najczęściej wykorzystywanymi narzędziami do obliczania długości odcinków w graniastosłupach są:

Twierdzenie Pitagorasa: a² + b² = c² – stosujemy je w trójkątach prostokątnych. Pamiętajcie, żeby zidentyfikować trójkąt prostokątny w figurze!
Wzory na przekątne wielokątów: Np. przekątna kwadratu o boku *a* ma długość *a√2*, przekątna prostokąta o bokach *a* i *b* ma długość √(a² + b²).
Wzory na pole powierzchni i objętość graniastosłupa: Czasami, znając pole powierzchni lub objętość, można wyznaczyć długość brakującego odcinka.
Trygonometria (funkcje sinus, cosinus, tangens): Jeśli znamy kąty w graniastosłupie, możemy użyć trygonometrii do obliczenia długości odcinków.

Przykład

Mamy prostopadłościan o wymiarach: długość 6 cm, szerokość 8 cm, wysokość 10 cm. Oblicz długość przekątnej tego prostopadłościanu.

Najpierw obliczamy długość przekątnej podstawy (prostokąta): d = √(6² + 8²) = √(36 + 64) = √100 = 10 cm.
Następnie, używamy przekątnej podstawy i wysokości prostopadłościanu jako przyprostokątnych w trójkącie prostokątnym, którego przeciwprostokątną jest przekątna prostopadłościanu: D = √(10² + 10²) = √(100 + 100) = √200 = 10√2 cm.

Częste błędy i jak ich unikać

W zadaniach z graniastosłupami często pojawiają się pewne pułapki. Oto kilka z nich i sposoby na ich uniknięcie:

Pomylenie krawędzi podstawy z krawędzią boczną: Pamiętajcie, że krawędzie podstawy tworzą wielokąt będący podstawą, a krawędzie boczne łączą podstawy.
Zastosowanie twierdzenia Pitagorasa w nieodpowiednim miejscu: Upewnijcie się, że trójkąt, w którym chcecie zastosować twierdzenie Pitagorasa, jest prostokątny!
Zapominanie o jednostkach: Zawsze podawajcie jednostki długości (cm, m, mm, itd.) w odpowiedzi.
Niedokładne rysunki: Starajcie się rysować schludne rysunki pomocnicze. Pomagają one zidentyfikować odpowiednie odcinki i trójkąty.

Przeciwwskazania i alternatywne perspektywy

Niektórzy uczniowie mogą uważać, że nauka o graniastosłupach jest zbędna, bo "nigdy się im to nie przyda". To błędne myślenie! Geometria rozwija wyobraźnię przestrzenną, logiczne myślenie i umiejętność rozwiązywania problemów. Te umiejętności przydadzą się w wielu dziedzinach życia, niezależnie od wybranej ścieżki kariery.

Inni mogą twierdzić, że uczenie się wzorów na pamięć to jedyna droga. Ja uważam, że ważniejsze jest zrozumienie, skąd te wzory się biorą, i umiejętność ich wyprowadzenia. Wtedy nie trzeba będzie się martwić, że coś się zapomni.

Rozwiązania i dalsze kroki

Aby lepiej zrozumieć odcinki w graniastosłupach, polecam:

Rozwiązywanie zadań: Im więcej zadań rozwiążecie, tym lepiej utrwalicie wiedzę.
Korzystanie z interaktywnych symulacji: W Internecie znajdziecie wiele symulacji graniastosłupów, które pozwalają na interaktywne manipulowanie bryłami i obserwowanie zależności między odcinkami.
Współpracę z kolegami: Wspólne rozwiązywanie zadań i dyskusja o problemach może pomóc w zrozumieniu trudnych zagadnień.
Zadawanie pytań nauczycielowi: Nie bójcie się pytać! Nauczyciel jest po to, żeby Wam pomóc.

Pamiętajcie, że nauka geometrii to proces. Nie zrażajcie się trudnościami. Z cierpliwością i systematycznością na pewno osiągniecie sukces.

Mam nadzieję, że ten artykuł pomógł Wam lepiej zrozumieć temat odcinków w graniastosłupach. Czy macie jakieś pytania? Gotowi na kolejne wyzwania geometryczne?