Od Czego Zależy Rodzaj Obrazu Otrzymanego W Zwierciadle Kulistym Wklęsłym

Dobrze, posłuchajcie uważnie, bo temat zwierciadeł kulistych wklęsłych to esencja optyki, a zrozumienie, od czego zależy obraz, który widzimy, to klucz do całego zagadnienia. Nie ma tu miejsca na uproszczenia, więc zaczynamy!

Rodzaj obrazu w zwierciadle kulistym wklęsłym jest wypadkową kilku fundamentalnych czynników, które splatają się w skomplikowany taniec promieni świetlnych. Kluczowe parametry, które determinują, czy obraz będzie rzeczywisty, pozorny, powiększony, pomniejszony, czy odwrócony, to przede wszystkim: odległość przedmiotu od zwierciadła (p), ogniskowa zwierciadła (f) oraz w mniejszym stopniu rozmiar samego przedmiotu.

Zacznijmy od najważniejszego: odległości przedmiotu od zwierciadła (p). To ona inicjuje całą kaskadę zależności. Ogniskowa zwierciadła (f) jest stała dla danego zwierciadła i definiuje punkt, w którym promienie równoległe do osi optycznej zwierciadła skupiają się po odbiciu. Teraz zaczyna się zabawa.

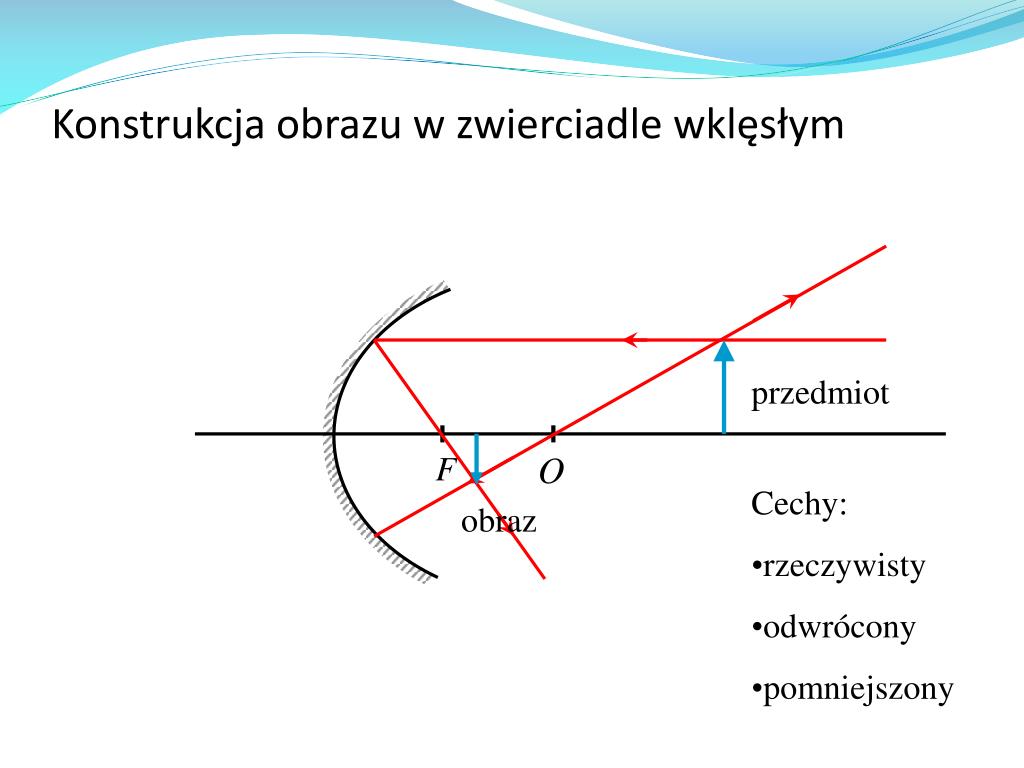
Jeśli p > 2f, czyli przedmiot znajduje się w odległości większej niż podwójna ogniskowa, otrzymamy obraz rzeczywisty, odwrócony i pomniejszony. Promienie świetlne wychodzące z przedmiotu, po odbiciu od zwierciadła, przecinają się przed zwierciadłem, tworząc fizyczny obraz, który możemy zaobserwować na ekranie (jeśli go umieścimy w odpowiednim miejscu). Obraz jest odwrócony, co oznacza, że góra przedmiotu pojawia się na dole obrazu, a dół na górze. Co więcej, obraz jest pomniejszony, co oznacza, że jest mniejszy niż sam przedmiot. To jest klasyczny przypadek wykorzystywany w projektorach.

Jeśli p = 2f, czyli przedmiot znajduje się dokładnie w odległości równej podwójnej ogniskowej, otrzymamy obraz rzeczywisty, odwrócony i tej samej wielkości. Promienie świetlne, po odbiciu, przetną się w odległości 2f po drugiej stronie zwierciadła. To szczególny przypadek, gdzie obraz jest dokładnie tak duży jak przedmiot.

Jeśli f < p < 2f, czyli przedmiot znajduje się pomiędzy ogniskową a podwójną ogniskową, otrzymamy obraz rzeczywisty, odwrócony i powiększony. Promienie świetlne przecinają się za podwójną ogniskową, dając nam obraz, który możemy zaobserwować na ekranie. Ten obraz jest odwrócony i większy niż sam przedmiot. To jest konfiguracja używana często w urządzeniach powiększających, gdzie potrzebujemy zobaczyć małe detale.

To, co dzieje się, gdy p = f, czyli przedmiot znajduje się w ognisku, jest fundamentalne. W tym przypadku promienie odbite od zwierciadła stają się równoległe do osi optycznej. Nie przecinają się, więc nie tworzy się obraz. Mówimy, że obraz powstaje w nieskończoności.

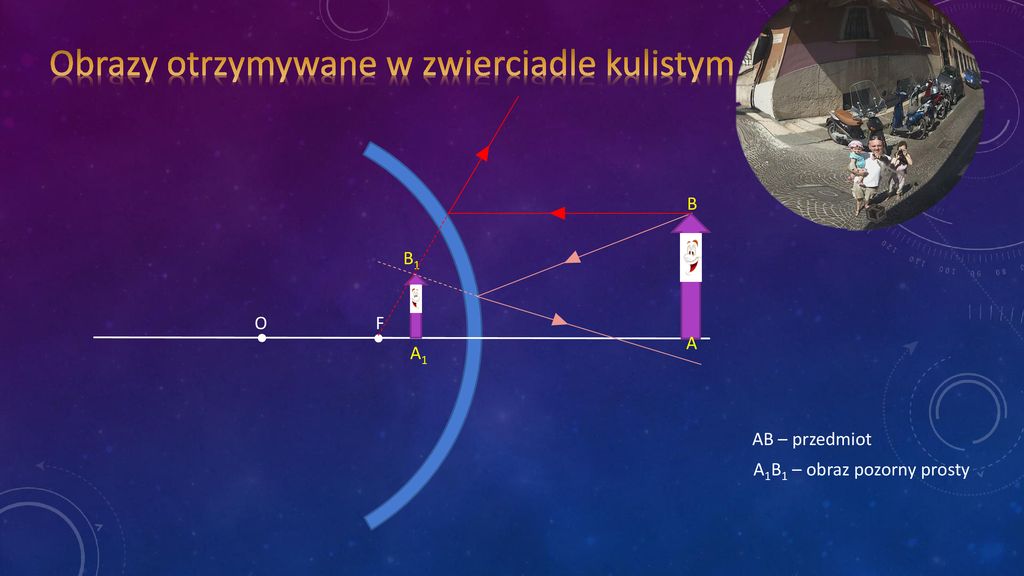
Najciekawsze dzieje się, gdy p < f, czyli przedmiot znajduje się bliżej zwierciadła niż jego ogniskowa. Wtedy otrzymujemy obraz pozorny, prosty i powiększony. Promienie odbite od zwierciadła rozbiegają się. Nasz mózg interpretuje to tak, jakby promienie wychodziły z punktu za zwierciadłem. Obraz pozorny nie powstaje przez fizyczne przecięcie się promieni, więc nie możemy go zobaczyć na ekranie. Widzimy go, patrząc w zwierciadło. Obraz jest prosty, czyli nieodwrócony, i powiększony. To jest zasada działania lupy.

Ale to nie wszystko! Wpływ na charakterystykę obrazu ma również rozmiar przedmiotu. Dla bardzo dużych przedmiotów, gdzie ich rozmiar jest porównywalny z ogniskową zwierciadła, możemy obserwować pewne zniekształcenia obrazu, wynikające z tego, że przybliżenie paraksjalne, które zakłada, że kąty padania i odbicia są małe, przestaje być dokładne. W skrajnych przypadkach prowadzi to do aberracji sferycznej, która rozmywa obraz.

Dodatkowo, jakość powierzchni zwierciadła odgrywa kluczową rolę. Idealnie gładka powierzchnia odbija światło w sposób uporządkowany, tworząc ostry obraz. Wszelkie niedoskonałości, rysy, czy nierówności powodują rozproszenie światła, co skutkuje mniej wyraźnym obrazem.

H2: Równania i zależności matematyczne

Opisane powyżej zależności można wyrazić matematycznie za pomocą równania soczewki (zwierciadła):

1/f = 1/p + 1/q

gdzie:

• f - ogniskowa zwierciadła
• p - odległość przedmiotu od zwierciadła
• q - odległość obrazu od zwierciadła

Znak 'q' decyduje o tym, czy obraz jest rzeczywisty (q > 0) czy pozorny (q < 0).

Powiększenie (M) definiuje się jako stosunek wysokości obrazu (h') do wysokości przedmiotu (h):

M = h'/h = -q/p

Znak powiększenia określa, czy obraz jest prosty (M > 0) czy odwrócony (M < 0). Wartość bezwzględna powiększenia mówi nam, czy obraz jest powiększony (|M| > 1) czy pomniejszony (|M| < 1).

Te równania pozwalają nam dokładnie obliczyć położenie obrazu i jego powiększenie, znając ogniskową zwierciadła i odległość przedmiotu.

H2: Zastosowania praktyczne

Zrozumienie zależności między położeniem przedmiotu a rodzajem obrazu w zwierciadle kulistym wklęsłym ma ogromne znaczenie praktyczne. Wykorzystuje się to w wielu urządzeniach, takich jak:

• Lupy: Dają powiększony, pozorny obraz, gdy przedmiot znajduje się bliżej niż ogniskowa.
• Reflektory: Umieszczenie źródła światła w ognisku zwierciadła powoduje, że odbite promienie są równoległe, tworząc silny strumień światła.
• Teleskopy: Zwierciadła w teleskopach skupiają światło od odległych obiektów, tworząc powiększony obraz.
• Lustra kosmetyczne: Często stosuje się zwierciadła wklęsłe, aby uzyskać powiększony obraz twarzy podczas makijażu.
• Projektory: Wykorzystują fakt, że obraz rzeczywisty, odwrócony i pomniejszony może być wyświetlany na ekranie.
• Lampy solarne skupiające światło: w systemach koncentrujących energię słoneczną, gdzie odpowiednio ukształtowane zwierciadło skupia promienie słoneczne w jednym punkcie, generując wysoką temperaturę.

H2: Ograniczenia i Aberracje

Należy pamiętać, że przedstawiona teoria opiera się na przybliżeniach, które nie zawsze są spełnione w praktyce. Jednym z ważniejszych ograniczeń jest aberracja sferyczna, która pojawia się, gdy promień światła pada na zwierciadło w dużej odległości od osi optycznej. Wtedy promień skupia się nie dokładnie w ognisku, a w pewnym punkcie przed ogniskiem. Im większa apertura (średnica) zwierciadła, tym bardziej widoczna jest aberracja sferyczna.

Kolejnym rodzajem aberracji jest aberracja komatyczna, która powoduje, że obraz punktowego źródła światła przyjmuje kształt komety. Jest to spowodowane różnicami w powiększeniu dla różnych części zwierciadła.

Ponadto, astygmatyzm powoduje, że obraz punktu poza osią optyczną jest rozmazany i ma kształt linii. Wszystkie te aberracje ograniczają jakość obrazu uzyskiwanego za pomocą zwierciadeł kulistych. Aby zminimalizować te efekty, stosuje się specjalne techniki korekcji, takie jak wykorzystanie zwierciadeł parabolicznych lub kombinacji soczewek i zwierciadeł.

Podsumowując, rodzaj obrazu otrzymanego w zwierciadle kulistym wklęsłym zależy od subtelnej interakcji pomiędzy odległością przedmiotu od zwierciadła, ogniskową zwierciadła oraz jego charakterystyką. Opanowanie tych zależności jest kluczowe do zrozumienia optyki i projektowania efektywnych systemów optycznych. Pamiętajcie, teoria to jedno, ale prawdziwe zrozumienie przychodzi przez eksperymentowanie i obserwację. Zatem, do dzieła!