Obliczanie Miar Kątów Zadania Klasa 5

Witajcie, młodzi matematycy! Wkraczamy w fascynujący świat geometrii, a konkretnie – obliczania miar kątów! Temat ten jest niezwykle ważny w klasie 5, ponieważ stanowi fundament dla dalszej nauki i zrozumienia przestrzeni wokół nas. Nie martwcie się, jeśli na początku wydaje się to trudne – wspólnie przejdziemy przez wszystkie zagadnienia krok po kroku, aby wszystko stało się jasne i zrozumiałe. Gotowi? Zaczynamy!

Kąty – podstawowe pojęcia

Zanim zaczniemy obliczenia, musimy dobrze zrozumieć, czym w ogóle jest kąt. Wyobraź sobie dwie proste linie wychodzące z jednego punktu. Ten punkt nazywamy wierzchołkiem kąta, a linie – ramionami kąta. Obszar pomiędzy tymi ramionami to właśnie kąt.

Rodzaje kątów

Kąty dzielimy na kilka rodzajów, w zależności od ich miary, czyli od tego, jak bardzo są "otwarte" ramiona kąta. Najważniejsze z nich to:

Kąt ostry: Mniejszy niż 90 stopni. Wyobraź sobie mały kawałek pizzy.
Kąt prosty: Dokładnie 90 stopni. Róg kartki papieru to idealny przykład kąta prostego.
Kąt rozwarty: Większy niż 90 stopni, ale mniejszy niż 180 stopni. Trochę większy kawałek pizzy.
Kąt półpełny: Dokładnie 180 stopni. Tworzy prostą linię.
Kąt pełny: Dokładnie 360 stopni. Pełny obrót!

Zapamiętanie tych nazw i miar jest kluczowe, ponieważ będziemy ich używać w dalszych obliczeniach.

Mierzenie kątów – stopniowy świat

Miarę kąta wyrażamy w stopniach (symbol: °). Pełny okrąg ma 360 stopni. Wyobraź sobie, że kroisz pizzę na 360 równych kawałków – każdy kawałek to 1 stopień.

Do mierzenia kątów używamy specjalnego narzędzia – kątomierza. Kątomierz ma podziałkę, która pokazuje, ile stopni ma dany kąt. Nauka korzystania z kątomierza jest bardzo ważna, ale na szczęście w wielu zadaniach będziemy obliczać miary kątów, niekoniecznie je mierząc.

Obliczanie miar kątów – podstawowe zasady

Teraz przejdziemy do konkretnych przykładów obliczania miar kątów. Ważne jest, aby pamiętać o kilku podstawowych zasadach:

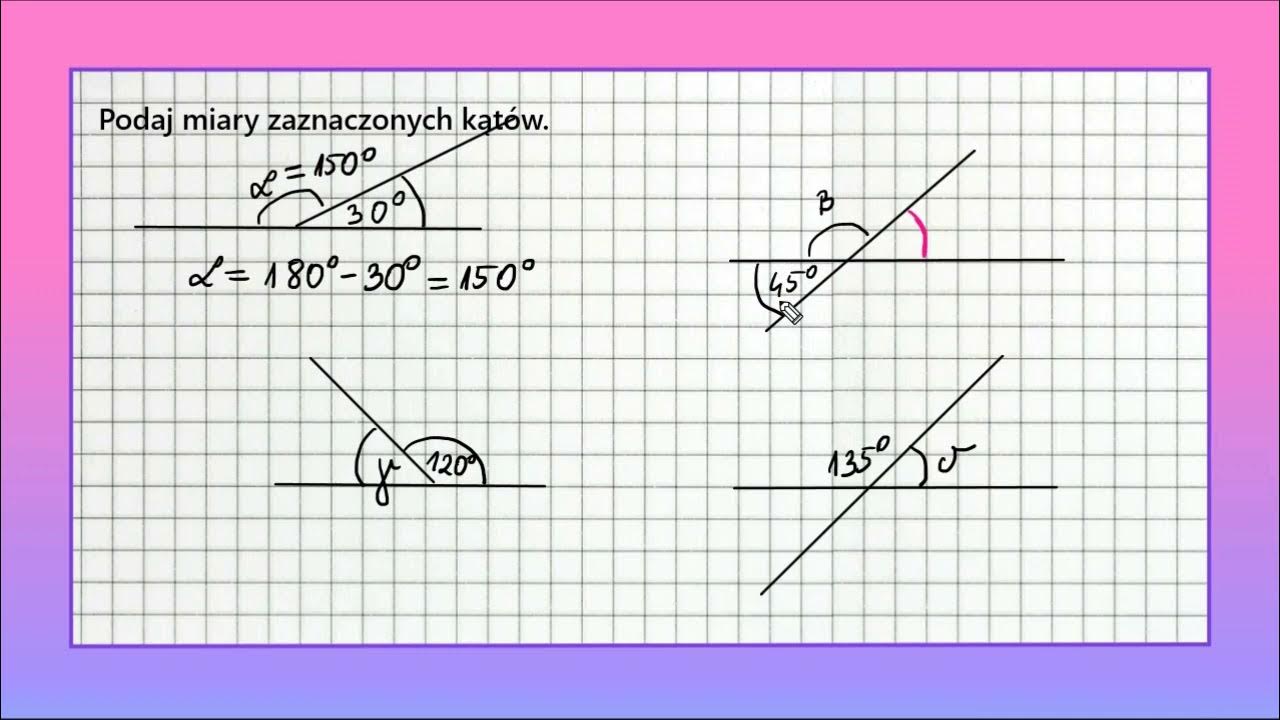
Suma kątów przyległych

Kąty przyległe to dwa kąty, które mają wspólny wierzchołek i jedno wspólne ramię, a ich ramiona nie będące wspólnymi tworzą linię prostą. Suma miar kątów przyległych wynosi zawsze 180 stopni. Na przykład, jeśli jeden z kątów przyległych ma miarę 60 stopni, to drugi ma miarę 180° - 60° = 120°.

Przykład: Wyobraź sobie, że stoisz na prostej drodze. Skręcasz w prawo o 75 stopni. O ile stopni musisz skręcić w lewo, aby zawrócić i iść w przeciwnym kierunku? Odpowiedź: 180° - 75° = 105°.

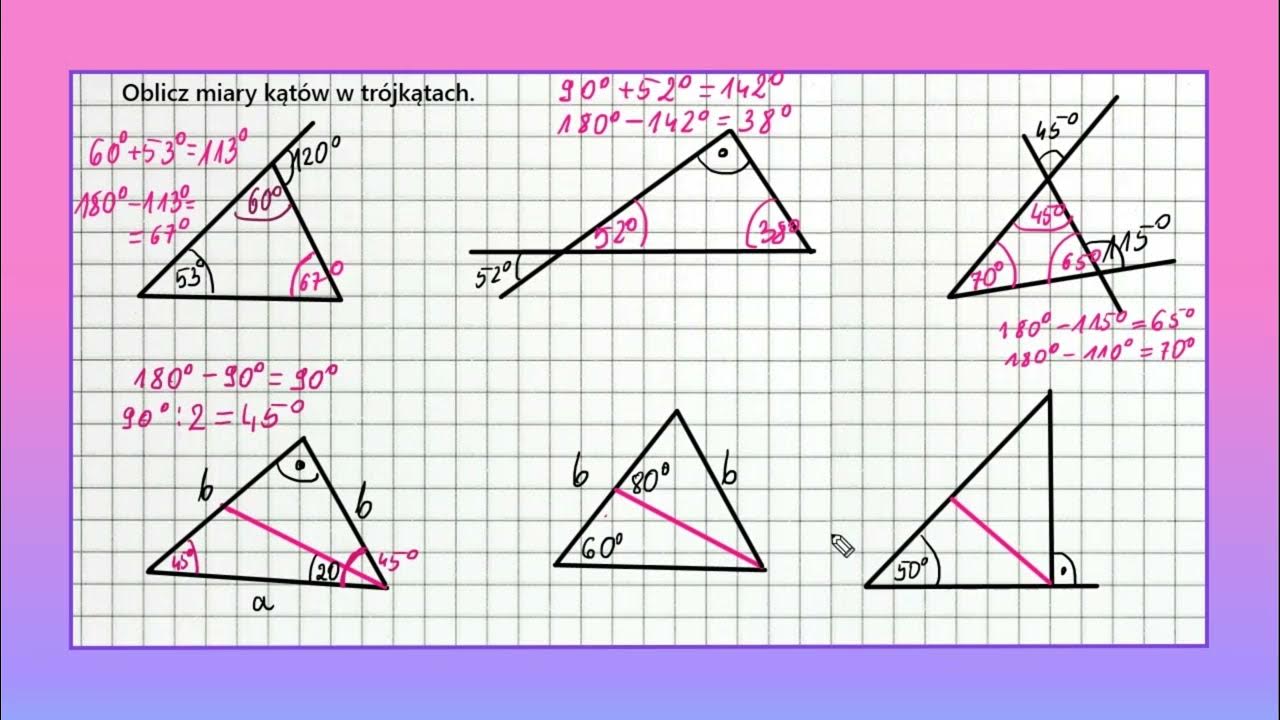
Suma kątów w trójkącie

Suma miar kątów wewnętrznych w każdym trójkącie wynosi 180 stopni. Oznacza to, że jeśli znamy miary dwóch kątów w trójkącie, możemy obliczyć miarę trzeciego kąta. Wystarczy odjąć sumę znanych kątów od 180 stopni.

Przykład: W trójkącie dwa kąty mają miary 40° i 80°. Ile wynosi miara trzeciego kąta? Odpowiedź: 180° - (40° + 80°) = 180° - 120° = 60°.

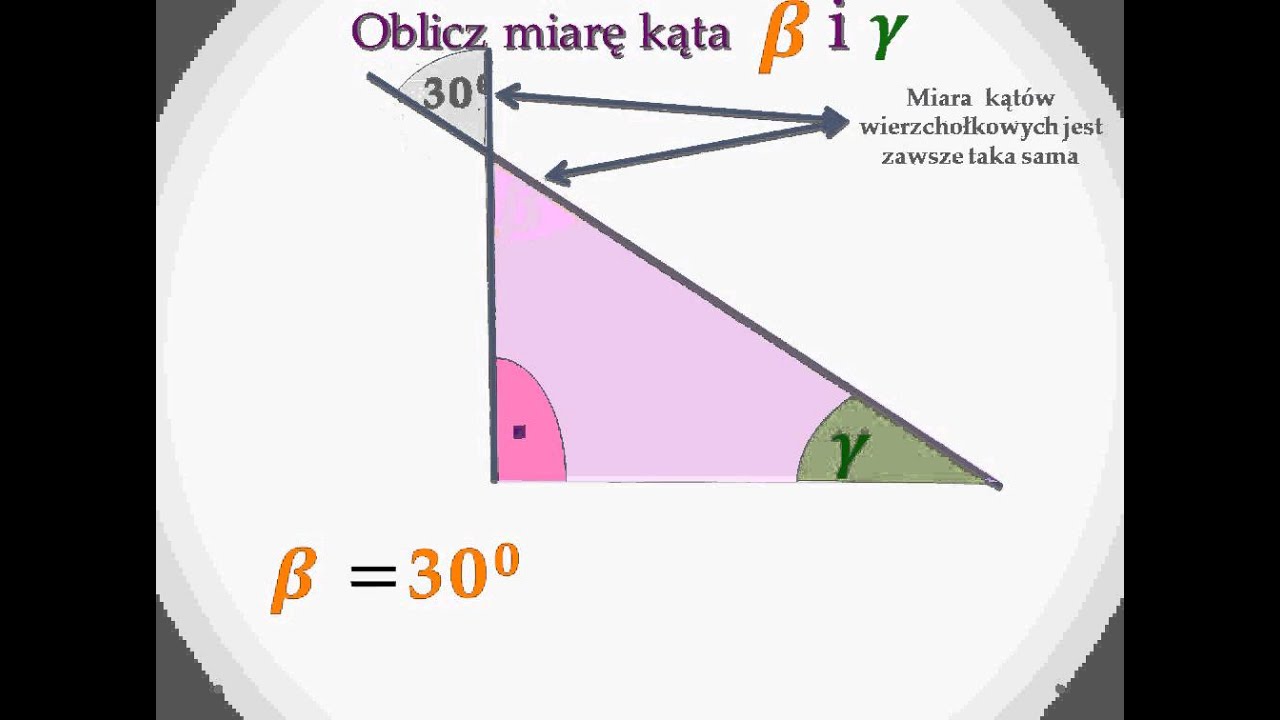
Kąty wierzchołkowe

Kąty wierzchołkowe to dwa kąty, które powstały w wyniku przecięcia się dwóch prostych. Kąty wierzchołkowe są równe. Wyobraź sobie znak "X" – kąty na górze i na dole są równe, a kąty po lewej i prawej również są równe.

Przykład: Dwie proste przecinają się. Jeden z kątów ma miarę 110°. Jaka jest miara kąta wierzchołkowego do niego? Odpowiedź: 110°.

Kąty odpowiadające i naprzemianległe (przy prostych równoległych)

Jeżeli mamy dwie proste równoległe przecięte trzecią prostą (nazywaną sieczną), to tworzą się różne pary kątów, które mają specjalne właściwości.

Kąty odpowiadające: Są równe. Znajdują się po tej samej stronie siecznej i w "odpowiednich" miejscach względem prostych równoległych.
Kąty naprzemianległe wewnętrzne: Są równe. Znajdują się po przeciwnych stronach siecznej i pomiędzy prostymi równoległymi.
Kąty naprzemianległe zewnętrzne: Są równe. Znajdują się po przeciwnych stronach siecznej i na zewnątrz prostych równoległych.

Przykład: Dwie proste równoległe przecina sieczna. Jeden z kątów odpowiadających ma miarę 65°. Ile wynosi miara drugiego kąta odpowiadającego? Odpowiedź: 65°.

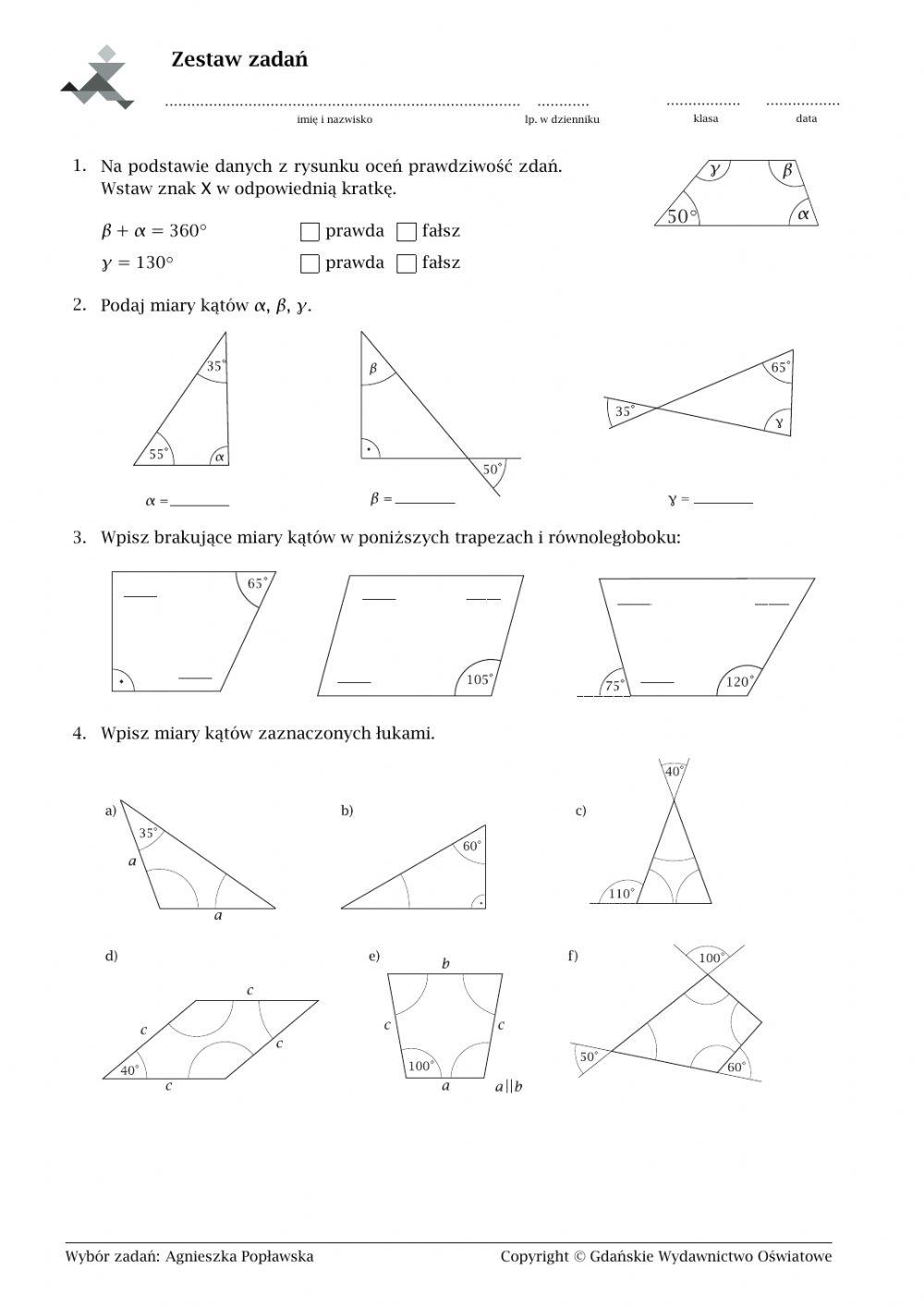
Przykładowe zadania z rozwiązaniami

Aby utrwalić zdobytą wiedzę, rozwiążemy kilka przykładowych zadań:

Zadanie 1: Oblicz miarę kąta α (alfa), jeśli kąt do niego przyległy ma miarę 135°.

Rozwiązanie: Wiemy, że suma kątów przyległych wynosi 180°. Zatem α = 180° - 135° = 45°.

Zadanie 2: W trójkącie jeden kąt ma miarę 90°, a drugi 30°. Ile wynosi miara trzeciego kąta?

Rozwiązanie: Suma kątów w trójkącie to 180°. Zatem trzeci kąt ma miarę 180° - (90° + 30°) = 180° - 120° = 60°.

Zadanie 3: Dwie proste przecinają się. Jeden z kątów wierzchołkowych ma miarę 72°. Ile wynosi miara drugiego kąta wierzchołkowego?

Rozwiązanie: Kąty wierzchołkowe są równe. Zatem drugi kąt ma miarę 72°.

Zadanie 4: Dwie proste równoległe przecina sieczna. Jeden z kątów odpowiadających ma miarę 115°. Ile wynosi miara drugiego kąta odpowiadającego?

Rozwiązanie: Kąty odpowiadające są równe. Zatem drugi kąt ma miarę 115°.

Praktyczne zastosowania obliczania miar kątów

Obliczanie miar kątów nie jest tylko abstrakcyjną zabawą matematyczną. Ma ono wiele praktycznych zastosowań w życiu codziennym, w różnych dziedzinach nauki i techniki. Przykłady:

Architektura i budownictwo: Architekci i inżynierowie muszą dokładnie obliczać kąty przy projektowaniu budynków, mostów i innych konstrukcji. Kąty wpływają na stabilność, wytrzymałość i estetykę budynku.
Nawigacja: Kapitanowie statków i piloci samolotów używają kątów do określania kierunku i pozycji. Systemy GPS również wykorzystują obliczenia kątów do lokalizacji.
Robotyka: Roboty przemysłowe często wykonują precyzyjne ruchy, które wymagają dokładnego obliczania kątów.
Grafika komputerowa i gry: Obliczanie kątów jest niezbędne do tworzenia realistycznych animacji i interakcji w grach komputerowych.
Astronomia: Astronomowie używają kątów do określania pozycji gwiazd i planet na niebie.

Wyobraź sobie cieślę budującego dom. Musi on dokładnie obliczyć kąty nachylenia dachu, aby zapewnić prawidłowe odprowadzanie wody i uniknąć przecieków. Bez znajomości geometrii i umiejętności obliczania kątów, budowa solidnego i funkcjonalnego domu byłaby niemożliwa!

Podsumowanie i dalsza nauka

Gratulacje! Dotarliście do końca artykułu o obliczaniu miar kątów. Mam nadzieję, że zdobyliście solidne podstawy i zrozumieliście najważniejsze zasady. Pamiętajcie, że praktyka czyni mistrza. Im więcej zadań rozwiążecie, tym lepiej zrozumiecie ten temat. Nie bójcie się pytać nauczyciela lub kolegów o pomoc, jeśli coś jest niejasne.

Kluczowe punkty do zapamiętania:

Różne rodzaje kątów (ostry, prosty, rozwarty, półpełny, pełny).
Suma kątów przyległych wynosi 180°.
Suma kątów w trójkącie wynosi 180°.
Kąty wierzchołkowe są równe.
Kąty odpowiadające i naprzemianległe (przy prostych równoległych) są równe.

Teraz Wasza kolej! Spróbujcie rozwiązać zadania z podręcznika lub z internetu. Poszukajcie w swoim otoczeniu przykładów kątów i spróbujcie oszacować ich miary. Im więcej będziecie ćwiczyć, tym pewniej będziecie się czuć w świecie geometrii.

Powodzenia!