Obliczanie Miar Kątów W Trójkącie

Zmagasz się z zadaniami z geometrii, a obliczanie miar kątów w trójkącie spędza Ci sen z powiek? Nie jesteś sam! Wielu uczniów, a nawet dorosłych, napotyka trudności z tym zagadnieniem. Na szczęście, zrozumienie kilku podstawowych zasad i opanowanie kilku prostych metod, może sprawić, że obliczanie kątów w trójkątach stanie się dziecinnie proste. Ten artykuł ma na celu rozwiać Twoje wątpliwości i dać Ci solidne podstawy do rozwiązywania zadań.

Podstawowe zasady – fundament Twojej wiedzy

Zanim przejdziemy do konkretnych przykładów, warto przypomnieć sobie dwie kluczowe zasady, które są absolutną podstawą obliczania miar kątów w trójkącie:

Suma kątów w każdym trójkącie wynosi 180 stopni. To fundamentalna zasada, od której wszystko się zaczyna. Niezależnie od tego, czy masz do czynienia z trójkątem równobocznym, równoramiennym czy różnobocznym – suma jego kątów wewnętrznych zawsze będzie wynosić 180°.
Rodzaje trójkątów a ich własności kątowe. Zrozumienie, z jakim typem trójkąta masz do czynienia, ułatwia rozwiązanie zadania. Na przykład:
- Trójkąt równoboczny: Wszystkie kąty mają miarę 60°.
- Trójkąt równoramienny: Kąty przy podstawie są równe.
- Trójkąt prostokątny: Jeden z kątów ma miarę 90°.

Zapamiętanie tych zasad to pierwszy krok do sukcesu! Pomyśl o nich jak o fundamentach domu – bez nich cała konstrukcja się zawali.

Obliczanie kątów – krok po kroku

Teraz przejdźmy do konkretnych metod i przykładów. Założymy, że znamy miary niektórych kątów i musimy obliczyć miary pozostałych.

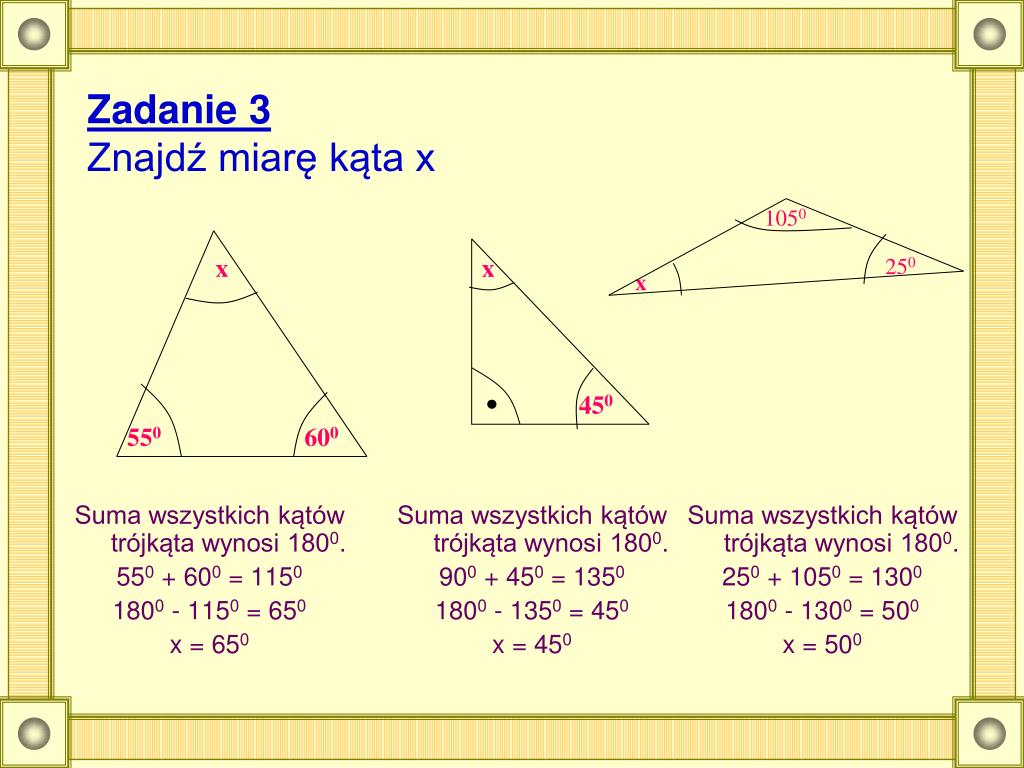
Przykład 1: Znane dwa kąty

Załóżmy, że w trójkącie ABC kąt A ma miarę 70°, a kąt B ma miarę 50°. Jak obliczyć miarę kąta C?

Użyj zasady sumy kątów w trójkącie: A + B + C = 180°
Podstaw znane wartości: 70° + 50° + C = 180°
Uprość równanie: 120° + C = 180°
Wylicz C: C = 180° - 120° = 60°

Zatem kąt C ma miarę 60°.

Przykład 2: Trójkąt równoramienny

W trójkącie równoramiennym KLM wiemy, że kąt przy wierzchołku K (między ramionami) ma miarę 40°. Jak obliczyć miary kątów przy podstawie (L i M)?

Zrozum, że kąty przy podstawie są równe: kąt L = kąt M
Użyj zasady sumy kątów w trójkącie: K + L + M = 180°
Podstaw znane wartości: 40° + L + L = 180° (ponieważ L = M)
Uprość równanie: 40° + 2L = 180°
Wylicz 2L: 2L = 180° - 40° = 140°
Wylicz L: L = 140° / 2 = 70°

Zatem kąt L i kąt M mają miarę 70°.

Przykład 3: Trójkąt prostokątny

W trójkącie prostokątnym PQR wiemy, że kąt prosty (P) ma miarę 90°, a kąt Q ma miarę 30°. Jak obliczyć miarę kąta R?

Użyj zasady sumy kątów w trójkącie: P + Q + R = 180°
Podstaw znane wartości: 90° + 30° + R = 180°
Uprość równanie: 120° + R = 180°
Wylicz R: R = 180° - 120° = 60°

Zatem kąt R ma miarę 60°.

Zaawansowane techniki i sztuczki

Oprócz podstawowych metod, istnieje kilka sztuczek, które mogą ułatwić rozwiązywanie bardziej skomplikowanych zadań.

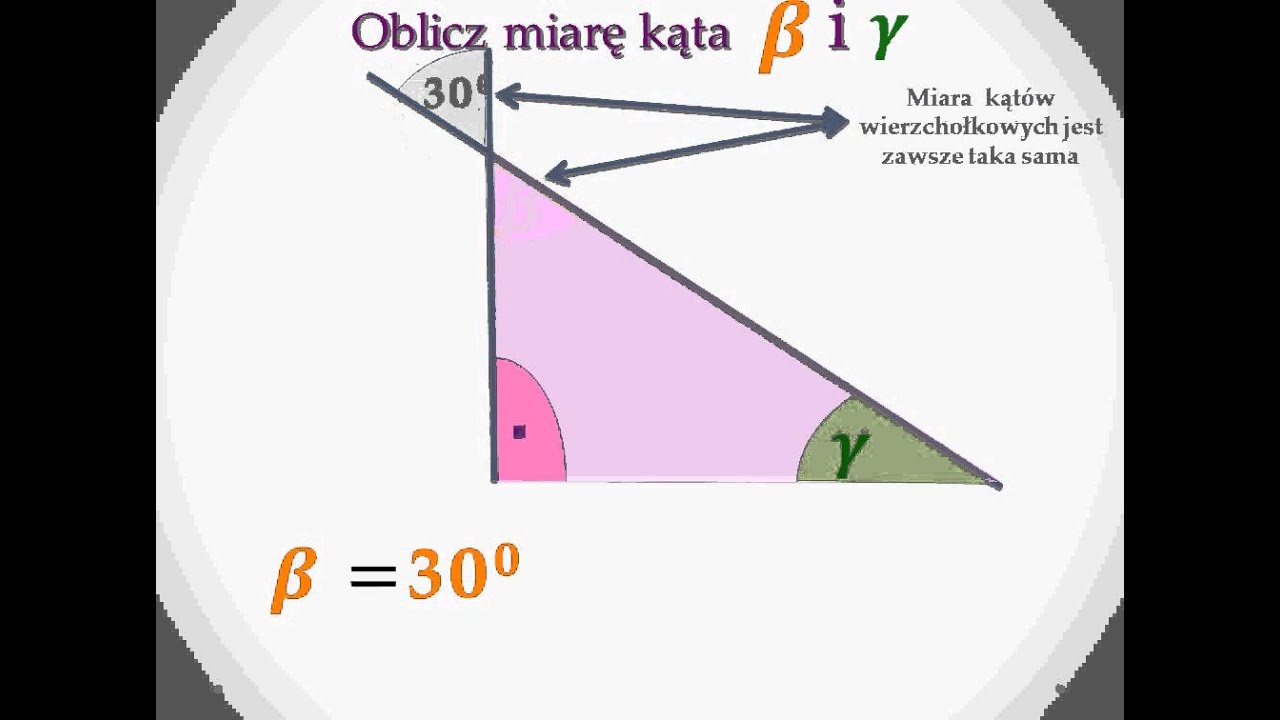
Kąty przyległe i wierzchołkowe

Zrozumienie relacji między kątami przyległymi i wierzchołkowymi może być kluczowe, zwłaszcza gdy trójkąty są połączone z innymi figurami geometrycznymi. Kąty przyległe to kąty, które mają wspólne ramię i wierzchołek, a ich suma wynosi 180°. Kąty wierzchołkowe to kąty leżące naprzeciwko siebie, utworzone przez przecięcie dwóch prostych – są one równe.

Twierdzenie o kącie zewnętrznym trójkąta

Twierdzenie o kącie zewnętrznym trójkąta mówi, że miara kąta zewnętrznego trójkąta jest równa sumie miar dwóch kątów wewnętrznych, które nie są do niego przyległe. Oznacza to, że jeśli masz trójkąt ABC, a kąt zewnętrzny przy wierzchołku A (nazwijmy go kątem D) jest utworzony przez przedłużenie boku AB, to miara kąta D jest równa sumie miar kątów B i C.

Wykorzystanie trygonometrii

W bardziej zaawansowanych zadaniach, zwłaszcza w trójkątach prostokątnych, trygonometria staje się nieocenionym narzędziem. Funkcje sinus, cosinus i tangens pozwalają na obliczanie miar kątów i długości boków, gdy znane są pewne relacje między nimi. Pamiętaj o definicjach tych funkcji: sin(α) = przeciwległy / przeciwprostokątna, cos(α) = przyległy / przeciwprostokątna, tan(α) = przeciwległy / przyległy.

Praktyczne wskazówki i porady

Oto kilka dodatkowych wskazówek, które mogą pomóc Ci w opanowaniu obliczania miar kątów w trójkącie:

Rysuj schematy! Zawsze zacznij od narysowania schematu trójkąta, nawet jeśli zadanie tego nie wymaga. Pomaga to wizualizować problem i lepiej zrozumieć relacje między kątami.
Oznaczaj wszystko! Oznacz wszystkie znane kąty i boki na schemacie. To ułatwi śledzenie danych i uniknięcie pomyłek.
Sprawdzaj swoje odpowiedzi! Po obliczeniu miar kątów, upewnij się, że ich suma wynosi 180°. Jeśli tak nie jest, oznacza to, że gdzieś popełniłeś błąd.
Ćwicz, ćwicz i jeszcze raz ćwicz! Geometria wymaga praktyki. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zasady i metody obliczania kątów.
Nie bój się prosić o pomoc! Jeśli utkniesz, nie wahaj się zapytać nauczyciela, kolegę lub poszukać pomocy online.

Dlaczego to jest ważne?

Może się zastanawiasz, po co w ogóle uczyć się obliczania kątów w trójkątach? Okazuje się, że ta wiedza ma szerokie zastosowanie w życiu codziennym i w różnych dziedzinach nauki. Od architektury i budownictwa, gdzie precyzyjne pomiary kątów są kluczowe dla stabilności konstrukcji, po nawigację i geodezję, gdzie obliczanie kątów pozwala na określanie pozycji i odległości. Nawet w grafice komputerowej i projektowaniu gier wideo znajomość geometrii jest niezbędna do tworzenia realistycznych trójwymiarowych obiektów i scen.

Podsumowanie

Obliczanie miar kątów w trójkącie może wydawać się trudne na początku, ale dzięki zrozumieniu podstawowych zasad, opanowaniu kilku prostych metod i regularnej praktyce, można stać się w tym naprawdę dobrym. Pamiętaj o zasadzie sumy kątów w trójkącie, rozpoznawaj rodzaje trójkątów i ich własności, i nie bój się korzystać z bardziej zaawansowanych technik, takich jak trygonometria. Przede wszystkim jednak, rysuj schematy, oznaczaj wszystko i ćwicz regularnie. Powodzenia!